2008 USAMO Problems/Problem 2
Contents
[hide]- 1 Problem
- 2 Solutions
- 2.1 Solution 1 (synthetic)
- 2.2 Solution 2 (complex)
- 2.3 Solution 3 (synthetic)
- 2.4 Solution 4 (synthetic)
- 2.5 Solution 5 (trigonometric)
- 2.6 Solution 6 (isogonal conjugates)
- 2.7 Solution 7 (symmedians)
- 2.8 Solution 8 (inversion) (Official Solution #2)
- 2.9 Solution 9 (Official Solution #1)
- 2.10 Solution 10 (Anti-Steiner point)
- 2.11 Solution 11 (Bary from EGMO)
- 3 See Also
Problem
(Zuming Feng) Let ![]() be an acute, scalene triangle, and let
be an acute, scalene triangle, and let ![]() ,
, ![]() , and
, and ![]() be the midpoints of
be the midpoints of ![]() ,
, ![]() , and
, and ![]() , respectively. Let the perpendicular bisectors of
, respectively. Let the perpendicular bisectors of ![]() and
and ![]() intersect ray
intersect ray ![]() in points
in points ![]() and
and ![]() respectively, and let lines
respectively, and let lines ![]() and
and ![]() intersect in point
intersect in point ![]() , inside of triangle
, inside of triangle ![]() . Prove that points
. Prove that points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() all lie on one circle.
all lie on one circle.
Solutions
Solution 1 (synthetic)
Without Loss of Generality, assume ![]() . It is sufficient to prove that
. It is sufficient to prove that ![]() , as this would immediately prove that
, as this would immediately prove that ![]() are concyclic.
By applying the Menelaus' Theorem in the Triangle
are concyclic.
By applying the Menelaus' Theorem in the Triangle ![]() for the transversal
for the transversal ![]() , we have (in magnitude)
, we have (in magnitude)
![]() Here, we used that
Here, we used that ![]() , as
, as ![]() is the midpoint of
is the midpoint of ![]() . Now, since
. Now, since ![]() and
and ![]() , we have
, we have
![]() Now, note that
Now, note that ![]() bisects the exterior
bisects the exterior ![]() and
and ![]() bisects exterior
bisects exterior ![]() , making
, making ![]() the
the ![]() -excentre of
-excentre of ![]() . This implies that
. This implies that ![]() bisects interior
bisects interior ![]() , making
, making ![]() , as was required.
, as was required.
Solution 2 (complex)
Let ![]() where
where ![]() all lie on the unit circle. Then
all lie on the unit circle. Then ![]() is 0. As noted earlier,
is 0. As noted earlier, ![]() is cyclic. We will find the ghost point
is cyclic. We will find the ghost point ![]() the second intersection of
the second intersection of ![]() and
and ![]() .
.
We know that these two circles already intersect at ![]() so we can reflect over the line between their centers. The center of
so we can reflect over the line between their centers. The center of ![]() is the midpoint of
is the midpoint of ![]() namely
namely ![]() . With the tangent formula and then taking the midpoint, we find that the center of
. With the tangent formula and then taking the midpoint, we find that the center of ![]() is
is ![]() Then we want to find the reflection of 0 over the line through
Then we want to find the reflection of 0 over the line through ![]() and
and ![]() Then we get
Then we get

Now it remains to show ![]() the other angle equality would follow by symmetry.
the other angle equality would follow by symmetry.
Then we get:
 Thus
Thus ![]() so
so ![]() and we're done.
and we're done.
~cocohearts
Solution 3 (synthetic)
![[asy] /* setup and variables */ size(280); pathpen = black + linewidth(0.7); pointpen = black; pen s = fontsize(8); pair B=(0,0),C=(5,0),A=(1,4); /* A.x > C.x/2 */ /* construction and drawing */ pair P=(A+B)/2,M=(B+C)/2,N=(A+C)/2,D=IP(A--M,P--P+5*(P-bisectorpoint(A,B))),E=IP(A--M,N--N+5*(bisectorpoint(A,C)-N)),F=IP(B--B+5*(D-B),C--C+5*(E-C)),O=circumcenter(A,B,C); D(MP("A",A,(0,1),s)--MP("B",B,SW,s)--MP("C",C,SE,s)--A--MP("M",M,s)); D(B--D(MP("D",D,NE,s))--MP("P",P,(-1,0),s)--D(MP("O",O,(0,1),s))); D(D(MP("E",E,SW,s))--MP("N",N,(1,0),s)); D(C--D(MP("F",F,NW,s))); D(B--O--C,linetype("4 4")+linewidth(0.7)); D(M--N,linetype("4 4")+linewidth(0.7)); D(rightanglemark(A,P,D,3.5));D(rightanglemark(A,N,E,3.5)); D(anglemark(B,A,C)); MP("y",A,(0,-6));MP("z",A,(4,-6)); D(anglemark(B,F,C,4),linewidth(0.6));D(anglemark(B,O,C,4),linewidth(0.6)); picture p = new picture; draw(p,circumcircle(B,O,C),linetype("1 4")+linewidth(0.7)); clip(p,B+(-5,0)--B+(-5,A.y+2)--C+(5,A.y+2)--C+(5,0)--cycle); add(p); /* D(circumcircle(A,P,N),linetype("4 4")+linewidth(0.7)); */ [/asy]](http://latex.artofproblemsolving.com/5/9/c/59c1afd86c69597587b940e9645c56d85342ba62.png)
Without loss of generality ![]() . The intersection of
. The intersection of ![]() and
and ![]() is
is ![]() , the circumcenter of
, the circumcenter of ![]() .
.
Let ![]() and
and ![]() . Note
. Note ![]() lies on the perpendicular bisector of
lies on the perpendicular bisector of ![]() , so
, so ![]() . So
. So ![]() . Similarly,
. Similarly, ![]() , so
, so ![]() . Notice that
. Notice that ![]() intercepts the minor arc
intercepts the minor arc ![]() in the circumcircle of
in the circumcircle of ![]() , which is double
, which is double ![]() . Hence
. Hence ![]() , so
, so ![]() is cyclic.
is cyclic.
Lemma. ![]() is directly similar to
is directly similar to ![]()
Proof.
![]() since
since ![]() ,
, ![]() ,
, ![]() are collinear,
are collinear, ![]() is cyclic, and
is cyclic, and ![]() . Also
. Also
![]() because
because ![]() , and
, and ![]() is the medial triangle of
is the medial triangle of ![]() so
so ![]() . Hence
. Hence ![]() .
.
Notice that ![]() since
since ![]() .
. ![]() . Then
. Then
![]() Hence
Hence ![]() .
.
Hence ![]() is similar to
is similar to ![]() by AA similarity. It is easy to see that they are oriented such that they are directly similar.
by AA similarity. It is easy to see that they are oriented such that they are directly similar.
End Lemma
![[asy] /* setup and variables */ size(280); pathpen = black + linewidth(0.7); pointpen = black; pen s = fontsize(8); pair B=(0,0),C=(5,0),A=(1,4); /* A.x > C.x/2 */ /* construction and drawing */ pair P=(A+B)/2,M=(B+C)/2,N=(A+C)/2,D=IP(A--M,P--P+5*(P-bisectorpoint(A,B))),E=IP(A--M,N--N+5*(bisectorpoint(A,C)-N)),F=IP(B--B+5*(D-B),C--C+5*(E-C)),O=circumcenter(A,B,C); D(MP("A",A,(0,1),s)--MP("B",B,SW,s)--MP("C",C,SE,s)--A--MP("M",M,s)); D(B--D(MP("D",D,NE,s))--MP("P",P,(-1,0),s)--D(MP("O",O,(1,0),s))); D(D(MP("E",E,SW,s))--MP("N",N,(1,0),s)); D(C--D(MP("F",F,NW,s))); D(B--O--C,linetype("4 4")+linewidth(0.7)); D(F--N); D(O--M); D(rightanglemark(A,P,D,3.5));D(rightanglemark(A,N,E,3.5)); /* commented in above asy D(circumcircle(A,P,N),linetype("4 4")+linewidth(0.7)); D(anglemark(B,A,C)); MP("y",A,(0,-6));MP("z",A,(4,-6)); D(anglemark(B,F,C,4),linewidth(0.6));D(anglemark(B,O,C,4),linewidth(0.6)); picture p = new picture; draw(p,circumcircle(B,O,C),linetype("1 4")+linewidth(0.7)); clip(p,B+(-5,0)--B+(-5,A.y+2)--C+(5,A.y+2)--C+(5,0)--cycle); add(p); */ [/asy]](http://latex.artofproblemsolving.com/f/2/1/f21402ee04f8bab4de4509f8e2cdcae9d4f26c5a.png)
By the similarity in the Lemma, ![]() .
. ![]() so
so ![]() by SAS similarity. Hence
by SAS similarity. Hence
![]() Using essentially the same angle chasing, we can show that
Using essentially the same angle chasing, we can show that ![]() is directly similar to
is directly similar to ![]() . It follows that
. It follows that ![]() is directly similar to
is directly similar to ![]() . So
. So
![]() Hence
Hence ![]() , so
, so ![]() is cyclic. In other words,
is cyclic. In other words, ![]() lies on the circumcircle of
lies on the circumcircle of ![]() . Note that
. Note that ![]() , so
, so ![]() is cyclic. In other words,
is cyclic. In other words, ![]() lies on the circumcircle of
lies on the circumcircle of ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() all lie on the circumcircle of
all lie on the circumcircle of ![]() . Hence
. Hence ![]() ,
, ![]() ,
, ![]() , and
, and ![]() lie on a circle, as desired.
lie on a circle, as desired.
Solution 4 (synthetic)
This solution utilizes the phantom point method. Clearly, APON are cyclic because ![]() . Let the circumcircles of triangles
. Let the circumcircles of triangles ![]() and
and ![]() intersect at
intersect at ![]() and
and ![]() .
.
Lemma. If ![]() are points on circle
are points on circle ![]() with center
with center ![]() , and the tangents to
, and the tangents to ![]() at
at ![]() intersect at
intersect at ![]() , then
, then ![]() is the symmedian from
is the symmedian from ![]() to
to ![]() .
.
Proof. This is fairly easy to prove (as H, O are isogonal conjugates, plus using SAS similarity), but the author lacks time to write it up fully, and will do so soon.
End Lemma
It is easy to see ![]() (the intersection of ray
(the intersection of ray ![]() and the circumcircle of
and the circumcircle of ![]() ) is colinear with
) is colinear with ![]() and
and ![]() , and because line
, and because line ![]() is the diameter of that circle,
is the diameter of that circle, ![]() , so
, so ![]() is the point
is the point ![]() in the lemma; hence, we may apply the lemma. From here, it is simple angle-chasing to show that
in the lemma; hence, we may apply the lemma. From here, it is simple angle-chasing to show that ![]() satisfies the original construction for
satisfies the original construction for ![]() , showing
, showing ![]() ; we are done.
; we are done.
Solution 5 (trigonometric)
By the Law of Sines, ![]() . Since
. Since ![]() and similarly
and similarly ![]() , we cancel to get
, we cancel to get ![]() . Obviously,
. Obviously, ![]() so
so ![]() .
.
Then ![]() and
and ![]() . Subtracting these two equations,
. Subtracting these two equations, ![]() so
so ![]() . Therefore,
. Therefore, ![]() (by AA similarity), so a spiral similarity centered at
(by AA similarity), so a spiral similarity centered at ![]() takes
takes ![]() to
to ![]() and
and ![]() to
to ![]() . Therefore, it takes the midpoint of
. Therefore, it takes the midpoint of ![]() to the midpoint of
to the midpoint of ![]() , or
, or ![]() to
to ![]() . So
. So ![]() and
and ![]() is cyclic.
is cyclic.
Solution 6 (isogonal conjugates)
![[asy] /* setup and variables */ size(280); pathpen = black + linewidth(0.7); pointpen = black; pen s = fontsize(8); pair B=(0,0),C=(5,0),A=(4,4); /* A.x > C.x/2 */ /* construction and drawing */ pair P=(A+B)/2,M=(B+C)/2,N=(A+C)/2,D=IP(A--M,P--P+5*(P-bisectorpoint(A,B))),E=IP(A--M,N--N+5*(bisectorpoint(A,C)-N)),F=IP(B--B+5*(D-B),C--C+5*(E-C)),O=circumcenter(A,B,C); D(MP("A",A,(0,1),s)--MP("B",B,SW,s)--MP("C",C,SE,s)--A--MP("M",M,s)); D(C--D(MP("E",E,NW,s))--MP("N",N,(1,0),s)--D(MP("O",O,SW,s))); D(D(MP("D",D,SE,s))--MP("P",P,W,s)); D(B--D(MP("F",F,s))); D(O--A--F,linetype("4 4")+linewidth(0.7)); D(MP("O'",circumcenter(A,P,N),NW,s)); D(circumcircle(A,P,N),linetype("4 4")+linewidth(0.7)); D(rightanglemark(A,P,D,3.5));D(rightanglemark(A,N,E,3.5)); picture p = new picture; draw(p,circumcircle(B,O,C),linetype("1 4")+linewidth(0.7)); draw(p,circumcircle(A,B,C),linetype("1 4")+linewidth(0.7)); clip(p,B+(-5,0)--B+(-5,A.y+2)--C+(5,A.y+2)--C+(5,0)--cycle); add(p); [/asy]](http://latex.artofproblemsolving.com/e/f/4/ef48251bf50ebbfa10db0114d80f3a0f7efe3276.png)
Construct ![]() on
on ![]() such that
such that ![]() . Then
. Then ![]() . Then
. Then ![]() , so
, so ![]() , or
, or ![]() . Then
. Then ![]() , so
, so ![]() . Then we have
. Then we have
![]() and
and ![]() . So
. So ![]() and
and ![]() are isogonally conjugate. Thus
are isogonally conjugate. Thus ![]() . Then
. Then
![]() .
.
If ![]() is the circumcenter of
is the circumcenter of ![]() then
then ![]() so
so ![]() is cyclic. Then
is cyclic. Then ![]() .
.
Then ![]() . Then
. Then ![]() is a right triangle.
is a right triangle.
Now by the homothety centered at ![]() with ratio
with ratio ![]() ,
, ![]() is taken to
is taken to ![]() and
and ![]() is taken to
is taken to ![]() . Thus
. Thus ![]() is taken to the circumcenter of
is taken to the circumcenter of ![]() and is the midpoint of
and is the midpoint of ![]() , which is also the circumcenter of
, which is also the circumcenter of ![]() , so
, so ![]() all lie on a circle.
all lie on a circle.
Solution 7 (symmedians)
Median ![]() of a triangle
of a triangle ![]() implies
implies ![]() .
Trig ceva for
.
Trig ceva for ![]() shows that
shows that ![]() is a symmedian.
Then
is a symmedian.
Then ![]() is a median, use the lemma again to show that
is a median, use the lemma again to show that ![]() , and similarly
, and similarly ![]() , so you're done.
, so you're done.
Solution 8 (inversion) (Official Solution #2)
Invert the figure about a circle centered at ![]() , and let
, and let ![]() denote the image of the point
denote the image of the point ![]() under this inversion. Find point
under this inversion. Find point ![]() so that
so that ![]() is a parallelogram and let
is a parallelogram and let ![]() denote the center of this parallelogram. Note that
denote the center of this parallelogram. Note that ![]() and
and ![]() . Because
. Because ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() , we also have
, we also have ![]() . Thus
. Thus
![]() Hence quadrilateral
Hence quadrilateral ![]() is cyclic and, by a similar argument, quadrilateral
is cyclic and, by a similar argument, quadrilateral ![]() is also cyclic. Because the images under the inversion of lines
is also cyclic. Because the images under the inversion of lines ![]() and
and ![]() are circles that intersect in
are circles that intersect in ![]() and
and ![]() , it follows that
, it follows that ![]() .
.
Next note that ![]() ,
, ![]() , and
, and ![]() are collinear and are the images of
are collinear and are the images of ![]() ,
, ![]() , and
, and ![]() , respectively, under a homothety centered at
, respectively, under a homothety centered at ![]() and with ratio
and with ratio ![]() . It follows that
. It follows that ![]() ,
, ![]() , and
, and ![]() are collinear, and then that the points
are collinear, and then that the points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() lie on a circle.
lie on a circle.
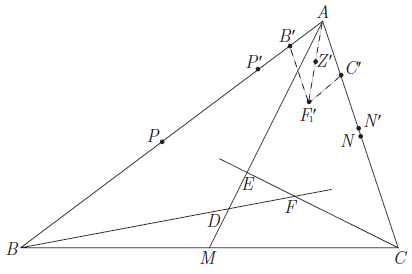
Solution 9 (Official Solution #1)
Let ![]() be the circumcenter of triangle
be the circumcenter of triangle ![]() . We prove that
. We prove that
![]() It will then follow that
It will then follow that ![]() lie on the circle with diameter
lie on the circle with diameter ![]() . Indeed, the fact that the first two angles in
. Indeed, the fact that the first two angles in ![]() are right is immediate because
are right is immediate because ![]() and
and ![]() are the perpendicular bisectors of
are the perpendicular bisectors of ![]() and
and ![]() , respectively. Thus we need only prove that
, respectively. Thus we need only prove that ![]() .
.
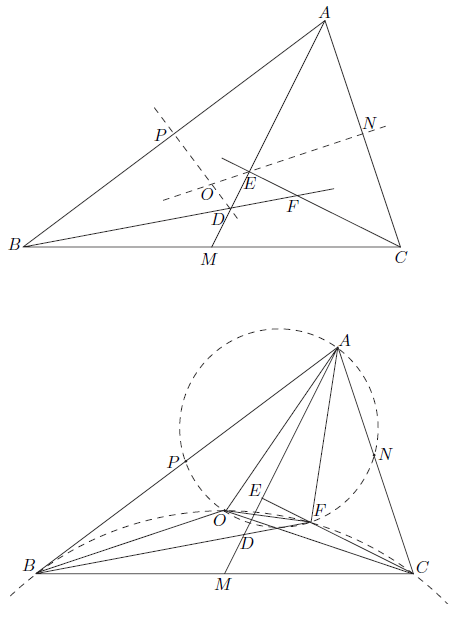
We may assume, without loss of generality, that ![]() . This leads to configurations similar to the ones shown above. The proof can be adapted to other configurations. Because
. This leads to configurations similar to the ones shown above. The proof can be adapted to other configurations. Because ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() , it follows that triangle
, it follows that triangle ![]() is an isosceles triangle with
is an isosceles triangle with ![]() . Likewise, triangle
. Likewise, triangle ![]() is isosceles with
is isosceles with ![]() . Let
. Let ![]() and
and ![]() , so
, so ![]() .
.
Applying the Law of Sines to triangles ![]() and
and ![]() gives
gives
![]() Taking the quotient of the two equations and noting that
Taking the quotient of the two equations and noting that ![]() , we find
, we find
![]() Because
Because ![]() , we have
, we have
![]() Applying the Law of Sines to triangles
Applying the Law of Sines to triangles ![]() and
and ![]() , we find
, we find
![]() Taking the quotient of the two equations yields
Taking the quotient of the two equations yields
![]() so by
so by ![]() ,
,
![]() Because
Because ![]() is an exterior angle to triangle
is an exterior angle to triangle ![]() , we have
, we have ![]() . Similarly,
. Similarly, ![]() . Hence
. Hence
![]() Thus
Thus ![]() , so
, so ![]() is cyclic. In addition,
is cyclic. In addition,
![]() and hence, from
and hence, from ![]() ,
, ![]() . Because
. Because ![]() is cyclic and
is cyclic and ![]() is isosceles with vertex angle
is isosceles with vertex angle ![]() , we have
, we have ![]() . Therefore,
. Therefore,
![]() This completes the proof.
This completes the proof.
Solution 10 (Anti-Steiner point)
First, let ![]() be the circumcenter of
be the circumcenter of ![]() . Note that since
. Note that since ![]() and
and ![]() , then
, then ![]() ,
, ![]() ,
, ![]() and
and ![]() , are concyclic.
, are concyclic.
Notice that ![]() and
and ![]() , which means
, which means ![]() . It follows analogously that
. It follows analogously that ![]() . This means that
. This means that ![]() is the orthocenter of triangle
is the orthocenter of triangle ![]() .
.
Now consider what happens when we reflect line ![]() over line
over line ![]() . Since
. Since ![]() is just the perpendicular bisector of
is just the perpendicular bisector of ![]() , point
, point ![]() will map to point
will map to point ![]() , and point
, and point ![]() , which is both line
, which is both line ![]() and
and ![]() , will map to itself. Therefore, we get line
, will map to itself. Therefore, we get line ![]() from this reflection. It follows analogously that by reflecting line
from this reflection. It follows analogously that by reflecting line ![]() over line
over line ![]() , we get
, we get ![]() .
.
Since line ![]() passes through
passes through ![]() , the orthocenter of triangle
, the orthocenter of triangle ![]() , its reflections over sides
, its reflections over sides ![]() and
and ![]() , which correspond to
, which correspond to ![]() and
and ![]() respectively, intersect on
respectively, intersect on ![]() (this is the Anti-Steiner point application). Therefore,
(this is the Anti-Steiner point application). Therefore, ![]() , the intersection of
, the intersection of ![]() and
and ![]() , lies on
, lies on ![]() .
.
Since ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are concyclic, then
are concyclic, then ![]() is the same as
is the same as ![]() , so
, so ![]() lies on
lies on ![]() , which is the same as saying
, which is the same as saying ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are concyclic, as desired.
are concyclic, as desired.
Solution 11 (Bary from EGMO)
First, we find the coordinates of ![]() . As
. As ![]() lies on
lies on ![]() , we know
, we know ![]() for some
for some ![]() . Now, we find
. Now, we find ![]()
Thus we obtain ![]()
(Note we are using Conway's notation here). Similarly, ![]() , and it follows that
, and it follows that ![]()
The sum of the coordinates of ![]() is
is ![]()
Hence, the reflection of ![]() over
over ![]() is simply
is simply ![]()
Then, it is obvious that ![]() lies on
lies on ![]() .
.
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See Also
- <url>viewtopic.php?t=202907 Discussion on AoPS/MathLinks</url>
| 2008 USAMO (Problems • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()









