2011 AMC 10B Problems/Problem 25
Contents
[hide]Problem
Let ![]() be a triangle with side lengths
be a triangle with side lengths ![]() and
and ![]() . For
. For ![]() , if
, if ![]() and
and ![]() and
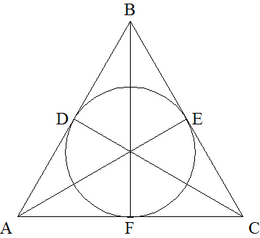
and ![]() are the points of tangency of the incircle of
are the points of tangency of the incircle of ![]() to the sides
to the sides ![]() , and
, and ![]() respectively, then
respectively, then ![]() is a triangle with side lengths
is a triangle with side lengths ![]() and
and ![]() if it exists. What is the perimeter of the last triangle in the sequence
if it exists. What is the perimeter of the last triangle in the sequence ![]() ?
?
![]()
Solution 1
By constructing the bisectors of each angle and the perpendicular radii of the incircle the triangle consists of 3 kites.
Hence ![]() and
and ![]() and
and ![]() . Let
. Let ![]() and
and ![]() gives three equations:
gives three equations:
![]()
![]()
![]()
(where ![]() for the first triangle.)
for the first triangle.)
Solving gives:
![]()
![]()
![]()
Subbing in gives that ![]() has sides of
has sides of ![]() .
.
![]() can easily be derived from this as the sides still differ by 1 hence the above solutions still work (now with
can easily be derived from this as the sides still differ by 1 hence the above solutions still work (now with ![]() ). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle.
). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle.
Subbing in gives ![]() with sides
with sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() has sides
has sides ![]() .
.
![]() would have sides
would have sides ![]() but these lengths do not make a
triangle as
but these lengths do not make a
triangle as
![]()
Likewise, you could create an equation instead of listing all the triangles to ![]() .
The sides of a triangle
.
The sides of a triangle ![]() would be
would be
![]() We then have
We then have
![]()
![]()
![]()
![]()
![]() Hence, the first triangle which does not exist in this sequence is
Hence, the first triangle which does not exist in this sequence is ![]() .
.
Hence the perimeter is
![]() .
.
Solution 2
Proceeding similarly to the first solution, we have that sides of each triangle are of the form ![]() for some number
for some number ![]() . Also, note that the perimeter of each triangle is half of the previous one. In order for the triangle to not exist, it must not satisfy the triangle inequality, meaning that
. Also, note that the perimeter of each triangle is half of the previous one. In order for the triangle to not exist, it must not satisfy the triangle inequality, meaning that ![]() . Then, the perimeter would be
. Then, the perimeter would be ![]() . So, to have a proper triangle, we have
. So, to have a proper triangle, we have ![]() . The first triangle to not work would have perimeter
. The first triangle to not work would have perimeter ![]() , thus the answer is
, thus the answer is ![]() .
.
Solution 3
This problem is a PoP(Power of Point) Bash exercise. What I did to solve this problem was look at recursive perimeters. The first ever perimeter is ![]() . Next, by PoP, inscribing the circle gives us three new lengths, namely
. Next, by PoP, inscribing the circle gives us three new lengths, namely ![]() . Denote
. Denote ![]() as
as ![]() and homogeneously the others. Then,
and homogeneously the others. Then, ![]() , and
, and ![]() . If we add all these equations up and divide by
. If we add all these equations up and divide by ![]() , we get
, we get ![]() . Writing this with
. Writing this with ![]() , we get that our new perimeter,
, we get that our new perimeter, ![]() , is indeed equal to
, is indeed equal to ![]() . Similarly, by the same concept, we get that
. Similarly, by the same concept, we get that ![]() and the pattern keeps going. In general, I found that for each new perimeter
and the pattern keeps going. In general, I found that for each new perimeter ![]() ,
, ![]() . Now, substituting in the numerical value of
. Now, substituting in the numerical value of ![]() , we get that
, we get that ![]() . If you keep dividing the numerator and denominator by 2, I got that:
. If you keep dividing the numerator and denominator by 2, I got that: ![]() . This representation of a new perimeter in terms of
. This representation of a new perimeter in terms of ![]() looks very similar to the option choices, so we're on the right path. Now, all we need to do is find out the last value of
looks very similar to the option choices, so we're on the right path. Now, all we need to do is find out the last value of ![]() when the sequence stops working. By the Triangular Inequality, we may be able to finish this off. Now, I won't go into depths here, but listing out terms and using the Triangular Inequality gives us:
First Sequence:
when the sequence stops working. By the Triangular Inequality, we may be able to finish this off. Now, I won't go into depths here, but listing out terms and using the Triangular Inequality gives us:
First Sequence:
![]()
![]()
![]() .
The ordered triple for this set of
.
The ordered triple for this set of ![]() is
is ![]() if you solve the PoP system of equations we got earlier. If you keep listing out terms, we can come up with the general form, and that is:
if you solve the PoP system of equations we got earlier. If you keep listing out terms, we can come up with the general form, and that is:
![]()
![]()
![]() .
The ordered triple for this set of
.
The ordered triple for this set of ![]() is
is ![]() . Now, if we plug in these values of
. Now, if we plug in these values of ![]() , and
, and ![]() into the inequalities, we see that the first two are always satisfied, but the last one is only satisfied when:
into the inequalities, we see that the first two are always satisfied, but the last one is only satisfied when:
![]() (You will get this if you simplify the last inequality). The last
(You will get this if you simplify the last inequality). The last ![]() for this to be satisfied is when
for this to be satisfied is when ![]() . If we go up to our general representation of
. If we go up to our general representation of ![]() , we see that
, we see that ![]() . Plugging in
. Plugging in ![]() because this is the last
because this is the last ![]() (and also the last triangle), we our final answer of
(and also the last triangle), we our final answer of ![]() or
or ![]() .
.
~ilikemath247365
See Also
Identical problem to the 2011 AMC 12B Problems/Problem 22.
| 2011 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 24 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()