2011 AMC 12B Problems/Problem 20
Contents
[hide]Problem
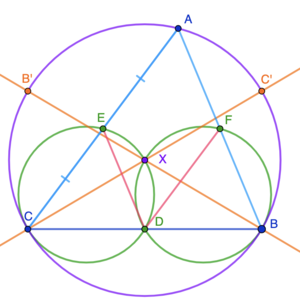
Triangle ![]() has
has ![]() , and
, and ![]() . The points
. The points ![]() , and
, and ![]() are the midpoints of
are the midpoints of ![]() , and
, and ![]() respectively. Let
respectively. Let ![]() be the intersection of the circumcircles of
be the intersection of the circumcircles of ![]() and
and ![]() . What is
. What is ![]() ?
?
![]()
Solution 1 (Coordinates)
Let us also consider the circumcircle of ![]() .
.
Note that if we draw the perpendicular bisector of each side, we will have the circumcenter of ![]() which is
which is ![]() , Also, since
, Also, since ![]() .
. ![]() is cyclic, similarly,
is cyclic, similarly, ![]() and
and ![]() are also cyclic. With this, we know that the circumcircles of
are also cyclic. With this, we know that the circumcircles of ![]() ,
, ![]() and
and ![]() all intersect at
all intersect at ![]() , so
, so ![]() is
is ![]() .
.
The question now becomes calculating the sum of the distance from each vertex to the circumcenter.
We can calculate the distances with coordinate geometry. (Note that ![]() because
because ![]() is the circumcenter.)
is the circumcenter.)
Let ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Then ![]() is on the line
is on the line ![]() and also the line with slope
and also the line with slope ![]() that passes through
that passes through ![]() (realize this is due to the fact that
(realize this is due to the fact that ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() ).
).
![]()
So ![]()
and 
Remark: the intersection of the three circles is called a Miquel point.
Solution 2 (Algebra)
Consider an additional circumcircle on ![]() . After drawing the diagram, it is noticed that each triangle has side values:
. After drawing the diagram, it is noticed that each triangle has side values: ![]() ,
, ![]() ,
, ![]() . Thus they are congruent, and their respective circumcircles are.
. Thus they are congruent, and their respective circumcircles are.
Let ![]() &
& ![]() be
be ![]() &
& ![]() 's circumcircles' respective centers. Since
's circumcircles' respective centers. Since ![]() &
& ![]() are congruent, the distance
are congruent, the distance ![]() &
& ![]() each are from
each are from ![]() are equal, so
are equal, so ![]() . The angle between
. The angle between ![]() &
& ![]() is
is ![]() , and since
, and since ![]() ,
, ![]() is also
is also ![]() .
. ![]() is a right triangle inscribed in a circle, so
is a right triangle inscribed in a circle, so ![]() must be the diameter of
must be the diameter of ![]() . Using the same logic & reasoning, we could deduce that
. Using the same logic & reasoning, we could deduce that ![]() &
& ![]() are also circumdiameters.
are also circumdiameters.
Since the circumcircles are congruent, circumdiameters ![]() ,
, ![]() , and
, and ![]() are congruent. Therefore, the solution can be found by calculating one of these circumdiameters and multiplying it by a factor of
are congruent. Therefore, the solution can be found by calculating one of these circumdiameters and multiplying it by a factor of ![]() . We can find the circumradius quite easily with the formula
. We can find the circumradius quite easily with the formula ![]() , such that
, such that ![]() and
and ![]() is the circumradius. Since
is the circumradius. Since ![]() :
:
![]()
After a few algebraic manipulations:
![]() .
.
Solution 3 (Dilation)
Let ![]() be the circumcenter of
be the circumcenter of ![]() and
and ![]() denote the length of the altitude from
denote the length of the altitude from ![]() Note that a dilation centered at
Note that a dilation centered at ![]() with ratio
with ratio ![]() takes the circumcircle of
takes the circumcircle of ![]() to the circumcircle of
to the circumcircle of ![]() . It also takes the point diametrically opposite
. It also takes the point diametrically opposite ![]() on the circumcircle of
on the circumcircle of ![]() to
to ![]() Therefore,
Therefore, ![]() lies on the circumcircle of
lies on the circumcircle of ![]() Similarly, it lies on the circumcircle of
Similarly, it lies on the circumcircle of ![]() By Pythagorean triples,
By Pythagorean triples, ![]() Finally, our answer is
Finally, our answer is ![]()
Solution 4 (basically Solution 1 but without coordinates)
Since Solution 1 has already proven that the circumcenter of ![]() coincides with
coincides with ![]() , we'll go from there. Note that the radius of the circumcenter of any given triangle is
, we'll go from there. Note that the radius of the circumcenter of any given triangle is ![]() , and since
, and since ![]() and
and ![]() , it can be easily seen that
, it can be easily seen that ![]() and therefore our answer is
and therefore our answer is ![]()
Solution 5
Since ![]() is a midline of
is a midline of ![]() we have that
we have that ![]() with a side length ratio of
with a side length ratio of ![]()
Consider a homothety of scale factor ![]() with on
with on ![]() concerning point
concerning point ![]() . Note that this sends
. Note that this sends ![]() to
to ![]() with
with ![]() By properties of homotheties,
By properties of homotheties, ![]() and
and ![]() are collinear. Similarly, we obtain that
are collinear. Similarly, we obtain that ![]() with all three points collinear. Let
with all three points collinear. Let ![]() denote the circumcenter of
denote the circumcenter of ![]() It is well-known that
It is well-known that ![]() and analogously
and analogously ![]() However, there is only one perpendicular line to
However, there is only one perpendicular line to ![]() passing through
passing through ![]() , therefore,
, therefore, ![]() coincides with
coincides with ![]()
It follows that ![]() where
where ![]() is the circumradius of
is the circumradius of ![]() and this can be computed using the formula
and this can be computed using the formula ![]() from which we quickly obtain
from which we quickly obtain ![]()
Solution 6 (Trigonometry)
![]() ,
, ![]() , as the angles are on the same circle.
, as the angles are on the same circle.
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
Therefore ![]() , and
, and ![]() is the angle bisector of
is the angle bisector of ![]() . By the angle bisector theorem
. By the angle bisector theorem ![]() ,
, ![]() . In a similar fashion
. In a similar fashion ![]() , where
, where ![]() is the circumcircle of
is the circumcircle of ![]() .
.
By the law of cosine, ![]() ,
, 
By the extended law of sines, ![]() ,
, ![]()
![]()
Solution 7 (abwabwabwa)
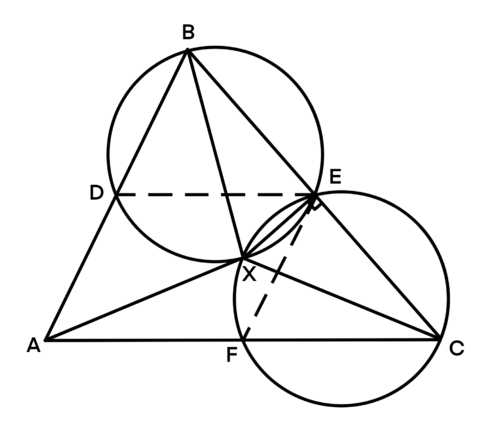
Claim, ![]() is the circumcenter of triangle
is the circumcenter of triangle ![]() .
.
Proof: Note that ![]() and
and ![]() are congruent. Consider the centers
are congruent. Consider the centers ![]() and
and ![]() of
of ![]() and
and ![]() , respectively. Let
, respectively. Let ![]() be the reflection of
be the reflection of ![]() over
over ![]() , and let
, and let ![]() be the reflection of
be the reflection of ![]() over
over ![]() . Since they form diameters, they must form right triangles
. Since they form diameters, they must form right triangles ![]() and
and ![]() . However, because
. However, because ![]() , C' and B' are the same point. Thus, one point lies on both circumcircles, so this point is
, C' and B' are the same point. Thus, one point lies on both circumcircles, so this point is ![]() . But then X lies on the perpendicular bisector of
. But then X lies on the perpendicular bisector of ![]() , and appyling this logic to all 3 sides,
, and appyling this logic to all 3 sides, ![]() must be the circumcenter.
must be the circumcenter.
Memorizing that the circumradius of a ![]() triangle is
triangle is ![]() , since
, since ![]() ,
, ![]() .
.
-skibbysiggy
See also
| 2011 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 19 |
Followed by Problem 21 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()