2014 AMC 10A Problems/Problem 22
Contents
[hide]- 1 Problem
- 2 Solution 1 (Trigonometry)
- 3 Solution 2 (No Trigonometry)
- 4 Solution 3 Quick Construction (No Trigonometry)
- 5 Solution 4 (No Trigonometry)
- 6 Solution 5
- 7 Solution 6 (Pure Euclidian Geometry)
- 8 Solution 7 (Pure Euclidian Geometry)
- 9 Solution 8 (Trigonometry)
- 10 Solution 9
- 11 Solution 10 Law of Cosines
- 12 Solution 11 (No Trigonometry)
- 13 Solution 12 (Tangent of Sum of Two Angles Formula)
- 14 Video Solution by Richard Rusczyk
- 15 See Also
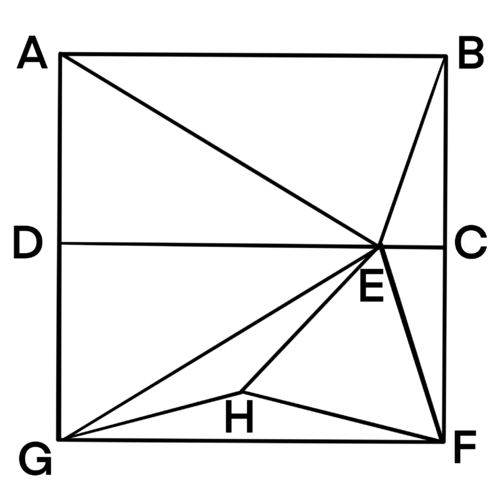
Problem
In rectangle ![]() ,
, ![]() and
and ![]() . Let
. Let ![]() be a point on
be a point on ![]() such that
such that ![]() . What is
. What is ![]() ?
?
![]()
Solution 1 (Trigonometry)
Note that ![]() . (It is important to memorize the sin, cos, and tan values of
. (It is important to memorize the sin, cos, and tan values of ![]() and
and ![]() .) Therefore, we have
.) Therefore, we have ![]() . Since
. Since ![]() is a
is a ![]() triangle,
triangle, ![]()
Solution 2 (No Trigonometry)
Let ![]() be a point on line
be a point on line ![]() such that points
such that points ![]() and
and ![]() are distinct and that
are distinct and that ![]() . By the angle bisector theorem,
. By the angle bisector theorem, ![]() . Since
. Since ![]() is a
is a ![]() right triangle,
right triangle, ![]() and
and ![]() . Additionally,
. Additionally, ![]() Now, substituting in the obtained values, we get
Now, substituting in the obtained values, we get  and
and ![]() . Substituting the first equation into the second yields
. Substituting the first equation into the second yields ![]() , so
, so ![]() . Because
. Because ![]() is a
is a ![]() triangle,
triangle, ![]() .
.
~edited by ripkobe_745
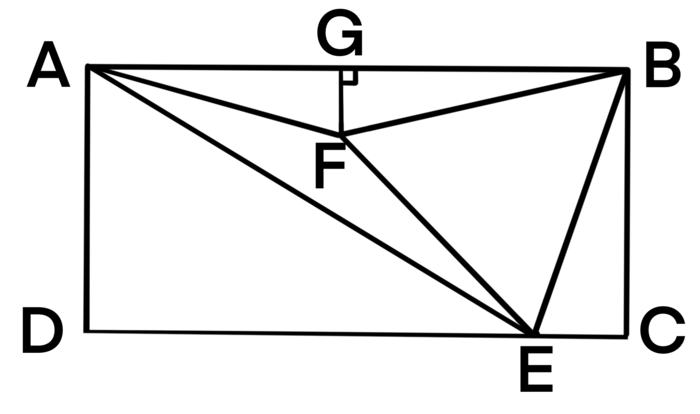
Solution 3 Quick Construction (No Trigonometry)
Reflect ![]() over line segment
over line segment ![]() . Let the point
. Let the point ![]() be the point where the right angle is of our newly reflected triangle. By subtracting
be the point where the right angle is of our newly reflected triangle. By subtracting ![]() to find
to find ![]() , we see that
, we see that ![]() is a
is a ![]() right triangle. By using complementary angles once more, we can see that
right triangle. By using complementary angles once more, we can see that ![]() is a
is a ![]() angle, and we've found that
angle, and we've found that ![]() is a
is a ![]() right triangle. From here, we can use the
right triangle. From here, we can use the ![]() properties of a
properties of a ![]() right triangle to see that
right triangle to see that ![]()
Solution 4 (No Trigonometry)
Let ![]() be a point on
be a point on ![]() such that
such that ![]() . Then
. Then ![]() Since
Since ![]() ,
, ![]() is isosceles.
is isosceles.
Let ![]() . Since
. Since ![]() is
is ![]() , we have
, we have ![]()
Since ![]() is isosceles, we have
is isosceles, we have ![]() . Since
. Since ![]() , we have
, we have ![]() Thus
Thus ![]() and
and ![]() .
.
Finally, by the Pythagorean Theorem, we have ![]()
~ Solution by Nafer
~ Edited by TheBeast5520
Note from williamgolly: When you find DE, note how ADE is congruent to a 30-60-90 triangle and you can easily find AE from there
Solution 5
First, divide all side lengths by ![]() to make things easier. We’ll multiply our answer by
to make things easier. We’ll multiply our answer by ![]() at the end.
Call side length
at the end.
Call side length ![]()
![]() . Using the Pythagorean Theorem, we can get side
. Using the Pythagorean Theorem, we can get side ![]() is
is ![]() .
.
The double angle identity for sine states that: ![]() So,
So, ![]() We know
We know ![]() . In triangle
. In triangle ![]() ,
, ![]() and
and ![]() . Substituting these in, we get our equation:
. Substituting these in, we get our equation: ![]() which simplifies to
which simplifies to ![]()
Now, using the quadratic formula to solve for ![]() .
. ![]() Because the length
Because the length ![]() must be close to one, the value of
must be close to one, the value of ![]() will be
will be ![]() .
We can now find
.
We can now find ![]() =
= ![]() and use it to find
and use it to find ![]() .
. ![]() .
To find
.
To find ![]() , we can use the Pythagorean Theorem with sides
, we can use the Pythagorean Theorem with sides ![]() and
and ![]() , OR we can notice that, based on the two side lengths we know,
, OR we can notice that, based on the two side lengths we know, ![]() is a
is a ![]() triangle. So
triangle. So ![]() .
.
Finally, we must multiply our answer by ![]() ,
, ![]() .
. ![]() .
.
~AWCHEN01
Solution 6 (Pure Euclidian Geometry)
We are going to use pure Euclidian geometry to prove ![]() .
.
Reflect rectangle ![]() along line
along line ![]() . Let the square be
. Let the square be ![]() as shown. Construct equilateral triangle
as shown. Construct equilateral triangle ![]() .
.
Because ![]() ,
, ![]() , and
, and ![]() ,
, ![]() by
by ![]() .
.
So, ![]() ,
, ![]() .
.
Because ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() by
by ![]() .
.
So, ![]() . By the reflection,
. By the reflection, ![]() .
. ![]()
This solution is inspired by AoPS "Introduction to Geometry" page 226 problem 8.22, and page 433 problem 16.42.
Solution 7 (Pure Euclidian Geometry)
We are going to use pure Euclidian geometry to prove ![]() .
.
Construct equilateral triangle ![]() , and let
, and let ![]() be the height of
be the height of ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() by
by ![]() .
.
![]() ,
, ![]() ,
, ![]() , by
, by ![]()
![]() .
.
So, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() by
by ![]() .
.
So, ![]()
Note: Similar to previous Solution
Solution 8 (Trigonometry)
All trigonometric functions in this solution are in degrees. We know ![]() so
so ![]()
![\[=\frac{\sqrt{2}}{2}\cdot\left(-\frac{\sqrt{3}}{2}\right)+\frac{1}{2}\cdot\frac{\sqrt{2}}{2}=\frac{-\sqrt{6}}{4}+\frac{\sqrt{2}}{4}=\frac{\sqrt{2}-\sqrt{6}}{4}\]](http://latex.artofproblemsolving.com/6/d/d/6dd4ed713c1c2e26e3cd180a0cfc11c2ff411c81.png)
![]() Let
Let ![]() , then
, then ![]() . By the definition of sine,
. By the definition of sine,
![]() Squaring both sides,
Squaring both sides,
![\[\frac{x^{2}}{x^{2}+100}=\frac{\left(\sqrt{2}-\sqrt{6}\right)^{2}}{16}=\frac{2-2\sqrt{12}+6}{16}=\frac{8-4\sqrt{3}}{16}=\frac{2-\sqrt{3}}{4}\]](http://latex.artofproblemsolving.com/a/4/b/a4bce7a0ac3bbaa7c9bb9e5bf9c2d8a264a3c8a6.png) Cross-multiplying,
Cross-multiplying,
![]() Simplifying,
Simplifying,
![]()
![\[x^{2}=\frac{200-100\sqrt{3}}{2+\sqrt{3}}=\frac{100\left(2-\sqrt{3}\right)}{2+\sqrt{3}}=100\cdot\frac{2-\sqrt{3}}{2+\sqrt{3}}\]](http://latex.artofproblemsolving.com/f/2/a/f2ad342cb3bbeff8bc9b8cca8436f83e2fd935cd.png) Let
Let ![]() . Notice that
. Notice that ![]() so
so ![]() .
. ![]() is then
is then ![\[\frac{2-\sqrt{3}}{2+\sqrt{3}}=\frac{\frac{1}{2+\sqrt{3}}}{2+\sqrt{3}}=\frac{1}{\left(2+\sqrt{3}\right)^{2}}\]](http://latex.artofproblemsolving.com/b/0/2/b02415e89db9bc008dce6d58979ea6cb0e3dbd8a.png) Recall that
Recall that
![]() which we now know is
which we now know is ![\[100\cdot\frac{1}{\left(2+\sqrt{3}\right)^{2}}=\frac{100}{\left(2+\sqrt{3}\right)^{2}}=\left(\frac{10}{2+\sqrt{3}}\right)^{2}\]](http://latex.artofproblemsolving.com/c/a/f/caf52fb5dd8db23c71f5e906e462d6a78c5ce186.png) Therefore
Therefore ![]() Rationalizing the denominator,
Rationalizing the denominator,
![\[\frac{10}{2+\sqrt{3}}\cdot\frac{2-\sqrt{3}}{2-\sqrt{3}}=\frac{20-10\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\]](http://latex.artofproblemsolving.com/7/c/b/7cb00e9d0d3f61799e128b9e339778fa7ee872d0.png) Which by difference of squares reduces to
Which by difference of squares reduces to
![]() so
so ![]() .
. ![]() is then
is then ![]() and since we know
and since we know ![]() , by the Pythagorean theorem,
, by the Pythagorean theorem, ![]() . The answer is
. The answer is ![]()
An alternate way to finish: since we know the lengths of ![]() and
and ![]() , we can figure out that
, we can figure out that ![]() and therefore
and therefore ![]() . Hence
. Hence ![]() is isosceles and
is isosceles and ![]() .
.
~JH. L
Solution 9
Similar to the others except that you find the base of the 15-75-90 triangle knowing that the side opposite side to 75 is 10, finding that you can subtract to find the base of the rectangle of the diagonal we are trying to find.
~YBSuburbanTea
Solution 10 Law of Cosines
The ratio between the side lengths of a 15, 75, 90 triangle are ![]() . Therefore,
. Therefore, ![]() . Using triangular ratios,
. Using triangular ratios, ![]() .
. ![]() .
.
From the law of cosines, ![]() .
.
So, ![]() .
.
At this stage, it is easier if we do not expand the numbers yet. Further simplifying, we have ![]() .
.
Now, we have ![]() .
.
Combing like terms, ![]() .
.
This equals, ![]() .
.
The ![]() cancel out each other. We are left with
cancel out each other. We are left with ![]() . So,
. So, ![]() .
~hwan
.
~hwan
Solution 11 (No Trigonometry)
Let ![]() be a point on line
be a point on line ![]() such that
such that ![]() . Also, set
. Also, set ![]() . In the isosceles triangle
. In the isosceles triangle ![]() ,
, ![]() . Thus in the right triangle
. Thus in the right triangle ![]() ,
, ![]() . Since
. Since ![]() ,
, ![]() and
and ![]() . Knowing that
. Knowing that ![]() , we have
, we have ![]() . Given that
. Given that ![]() , expressing using
, expressing using ![]() , we get
, we get ![]() . After dividing and rationalizing the denominator, we get
. After dividing and rationalizing the denominator, we get ![]() . Thus,
. Thus, ![]() . Using the Pythagorean theorem,
. Using the Pythagorean theorem, ![]() . Therefore, the answer choice is
. Therefore, the answer choice is ![]() .
.
Solution 12 (Tangent of Sum of Two Angles Formula)
Recall that ![]() . As in Solution 1, we want to find
. As in Solution 1, we want to find ![]() . Setting
. Setting ![]() , we get
, we get ![]() . We know that
. We know that ![]() , and now we can manipulate the equation to get a quadratic in
, and now we can manipulate the equation to get a quadratic in ![]() . (Do remember that
. (Do remember that ![]() because the denominator of the fraction cannot be equal to 0. However,
because the denominator of the fraction cannot be equal to 0. However, ![]() isn't equal to any of them, so it's okay to skip this part in this problem, but it is a good thing to do in general.) Solving the quadratic gives
isn't equal to any of them, so it's okay to skip this part in this problem, but it is a good thing to do in general.) Solving the quadratic gives ![]() . Clearly,
. Clearly, ![]() is positive, so we discard the negative solution and get
is positive, so we discard the negative solution and get ![]() . Then, we can proceed in the same way as Solution 1.
-scthecool
. Then, we can proceed in the same way as Solution 1.
-scthecool
Video Solution by Richard Rusczyk
https://www.youtube.com/watch?v=-GBvCLSfTuo
See Also
| 2014 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()