2014 IMO Problems/Problem 4
Contents
[hide]Problem
Points ![]() and
and ![]() lie on side
lie on side ![]() of acute-angled
of acute-angled ![]() so that
so that ![]() and
and ![]() . Points
. Points ![]() and
and ![]() lie on lines
lie on lines ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() . Prove that lines
. Prove that lines ![]() and
and ![]() intersect on the circumcircle of
intersect on the circumcircle of ![]() .
.
Solution
Solution 1
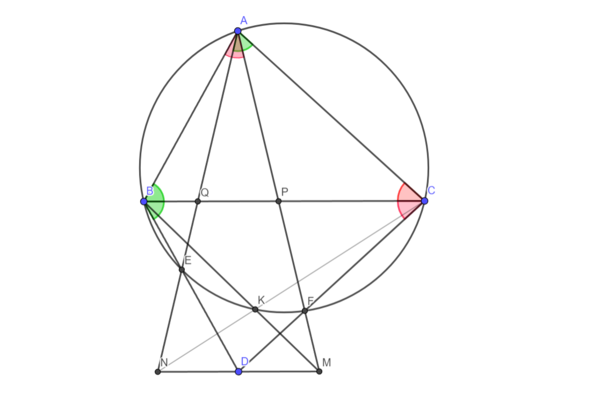
![[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki, go to User:Azjps/geogebra */ import graph; size(10.60000000000002cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -4.740000000000007, xmax = 16.46000000000002, ymin = -7.520000000000004, ymax = 4.140000000000004; /* image dimensions */ pen zzttqq = rgb(0.6000000000000006,0.2000000000000002,0.000000000000000); pen qqwuqq = rgb(0.000000000000000,0.3921568627450985,0.000000000000000); draw((1.800000000000002,3.640000000000004)--(-0.2200000000000002,-1.200000000000001)--(7.660000000000009,-1.140000000000001)--cycle, zzttqq); draw(arc((7.660000000000009,-1.140000000000001),0.6000000000000009,140.7958863822920,180.4362538499006)--(7.660000000000009,-1.140000000000001)--cycle, red); draw(arc((-0.2200000000000002,-1.200000000000001),0.6000000000000009,0.4362538499004549,67.34652063545073)--(-0.2200000000000002,-1.200000000000001)--cycle, qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-106.1141136177082,-39.20411361770813)--(1.800000000000002,3.640000000000004)--cycle, qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-112.6534793645495,-73.01347936454944)--(1.800000000000002,3.640000000000004)--cycle, red); /* draw figures */ draw((1.800000000000002,3.640000000000004)--(-0.2200000000000002,-1.200000000000001), zzttqq); draw((-0.2200000000000002,-1.200000000000001)--(7.660000000000009,-1.140000000000001), zzttqq); draw((7.660000000000009,-1.140000000000001)--(1.800000000000002,3.640000000000004), zzttqq); draw(arc((7.660000000000009,-1.140000000000001),0.6000000000000009,140.7958863822920,180.4362538499006), red); draw(arc((7.660000000000009,-1.140000000000001),0.5000000000000008,140.7958863822920,180.4362538499006), red); draw(arc((-0.2200000000000002,-1.200000000000001),0.6000000000000009,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((-0.2200000000000002,-1.200000000000001),0.5000000000000008,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((-0.2200000000000002,-1.200000000000001),0.4000000000000006,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.5000000000000008,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.4000000000000006,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-112.6534793645495,-73.01347936454944), red); draw(arc((1.800000000000002,3.640000000000004),0.5000000000000008,-112.6534793645495,-73.01347936454944), red); draw((-1.022670636276736,-6.130338243877306)--(7.660000000000009,-1.140000000000001)); draw((4.740746205921980,-5.986847110107199)--(-0.2200000000000002,-1.200000000000001)); draw((1.800000000000002,3.640000000000004)--(4.740746205921980,-5.986847110107199)); draw((1.800000000000002,3.640000000000004)--(-1.022670636276736,-6.130338243877306)); draw(circle((3.711084749329270,0.0008695880898521494), 4.110415438128883)); /* dots and labels */ dot((1.800000000000002,3.640000000000004),dotstyle); label("$A$", (1.880000000000002,3.760000000000004), NE * labelscalefactor); dot((-0.2200000000000002,-1.200000000000001),dotstyle); label("$B$", (-0.1400000000000008,-1.080000000000000), NE * labelscalefactor); dot((7.660000000000009,-1.140000000000001),dotstyle); label("$C$", (7.740000000000012,-1.020000000000000), NE * labelscalefactor); dot((0.3886646818616330,-1.245169121938651),dotstyle); label("$Q$", (0.4600000000000001,-1.120000000000000), NE * labelscalefactor); dot((3.270373102960991,-1.173423555053598),dotstyle); label("$P$", (3.360000000000004,-1.060000000000000), NE * labelscalefactor); dot((4.740746205921980,-5.986847110107199),dotstyle); label("$M$", (4.820000000000006,-5.860000000000003), NE * labelscalefactor); dot((-1.022670636276736,-6.130338243877306),dotstyle); label("$N$", (-0.9400000000000020,-6.020000000000004), NE * labelscalefactor); dot((2.709057008802497,-3.985539257126989),dotstyle); label("$D$", (2.780000000000003,-3.860000000000002), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]](http://latex.artofproblemsolving.com/0/8/8/088e13223b4887f9d60d871fc8c76363a0bed975.png)
We are trying to prove that the intersection of ![]() and
and ![]() , call it point
, call it point ![]() , is on the circumcircle of triangle
, is on the circumcircle of triangle ![]() . In other words, we are trying to prove
. In other words, we are trying to prove ![]() .
Let the intersection of
.
Let the intersection of ![]() and
and ![]() be point
be point ![]() , and the intersection of
, and the intersection of ![]() and
and ![]() be point
be point ![]() .
Let us assume
.
Let us assume ![]() . Note: This is circular reasoning. If
. Note: This is circular reasoning. If ![]() , then
, then ![]() should be equal to
should be equal to ![]() and
and ![]() . We can quickly prove that the triangles
. We can quickly prove that the triangles ![]() ,
, ![]() , and
, and ![]() are similar, so
are similar, so ![]() . We also see that
. We also see that ![]() . Also because angles
. Also because angles ![]() and
and ![]() and
and ![]() are equal, the triangles
are equal, the triangles ![]() and
and ![]() ,
, ![]() and
and ![]() must be two pairs of similar triangles. Therefore we must prove angles
must be two pairs of similar triangles. Therefore we must prove angles ![]() and
and ![]() and
and ![]() are equal.
We have angles
are equal.
We have angles ![]() . We also have
. We also have ![]() ,
, ![]() . Because the triangles
. Because the triangles ![]() and
and ![]() are similar, we have
are similar, we have ![]() , so triangles
, so triangles ![]() and
and ![]() are similar. So the angles
are similar. So the angles ![]() and
and ![]() and
and ![]() are equal and we are done.
are equal and we are done.
Solution 2
Let ![]() be the midpoint of
be the midpoint of ![]() . Easy angle chasing gives
. Easy angle chasing gives ![]() . Because
. Because ![]() is the midpoint of
is the midpoint of ![]() , the cotangent rule applied on triangle
, the cotangent rule applied on triangle ![]() gives us
gives us
![]() Hence, by the cotangent rule on
Hence, by the cotangent rule on ![]() , we have
, we have
![]() Because the period of cotangent is
Because the period of cotangent is ![]() , but angles are less than
, but angles are less than ![]() , we have
, we have ![]()
Similarly, we have ![]() Hence, if
Hence, if ![]() and
and ![]() intersect at
intersect at ![]() , then
, then ![]() by the Angle Sum in a Triangle Theorem. Hence,
by the Angle Sum in a Triangle Theorem. Hence, ![]() is cyclic, which is equivalent to the desired result.
is cyclic, which is equivalent to the desired result.
--Suli 23:27, 7 February 2015 (EST)
Solution 3
Let ![]() be the midpoint of
be the midpoint of ![]() . By AA Similarity, triangles
. By AA Similarity, triangles ![]() and
and ![]() are similar, so
are similar, so ![]() and
and ![]() . Similarly,
. Similarly, ![]() , and so triangle
, and so triangle ![]() is isosceles. Thus,
is isosceles. Thus, ![]() , and so
, and so ![]() . Dividing both sides by 2, we have
. Dividing both sides by 2, we have ![]() , or
, or
![]() But we also have
But we also have ![]() , so triangles
, so triangles ![]() and
and ![]() are similar by
are similar by ![]() similarity. In particular,
similarity. In particular, ![]() . Similarly,
. Similarly, ![]() , so
, so ![]() . In addition, angle sum in triangle
. In addition, angle sum in triangle ![]() gives
gives ![]() . Therefore, if we let lines
. Therefore, if we let lines ![]() and
and ![]() intersect at
intersect at ![]() , by Angle Sum in quadrilateral
, by Angle Sum in quadrilateral ![]() concave
concave ![]() , and so convex
, and so convex ![]() , which is enough to prove that
, which is enough to prove that ![]() is cyclic. This completes the proof.
is cyclic. This completes the proof.
![[asy] size(250); defaultpen(fontsize(8pt)); pair A = dir(110); pair B = dir(210); pair C = dir(330); pair Pp = rotate(50, A)*B; pair P = extension(A,Pp,B,C); pair Qp = rotate(-70, A)*C; pair Q = extension(A,Qp,B,C); pair M = rotate(180,P)*A; pair N = rotate(180,Q)*A; path c1 = circumcircle(A,B,C); pair T = IP(B--M,C--N); pair L = midpoint(B--C); draw(A--B--C--cycle^^B--Q--A--P^^Q--N--C^^P--M--B^^A--L); draw(c1); dot("$A$", A, dir(100)); dot("$B$", B, dir(-110)); dot("$C$", C, dir(-40)); dot("$P$", P, dir(50)); dot("$Q$", Q, dir(-170)); dot("$M$", M, dir(-50)); dot("$N$", N, dir(-140)); dot("$T$", T,dir(-90)); dot("$L$", L, dir(-120)); [/asy]](http://latex.artofproblemsolving.com/1/2/b/12bb205080ded2d4418e6d2e50a17bdb81f05d9f.png)
--Suli 10:38, 8 February 2015 (EST)
Solution 4
Let ![]() be the second intersection of
be the second intersection of ![]() with the circumcircle of
with the circumcircle of ![]() and
and ![]() the second intersection of
the second intersection of ![]() with the circumcircle of
with the circumcircle of ![]() By inscribed angles, the tangent at
By inscribed angles, the tangent at ![]() is parallel to
is parallel to ![]() Let
Let ![]() denote the point at infinity along line
denote the point at infinity along line ![]() Note that
Note that ![]() So,
So, ![]() is harmonic. Similarly, we can find
is harmonic. Similarly, we can find ![]() is harmonic. Therefore,
is harmonic. Therefore, ![]() which means that
which means that ![]() and
and ![]() intersect on the circumcircle.
intersect on the circumcircle. ![]()
Solution 5
We use barycentric coordinates. Due to the equal angles, ![]() is tangent to the circumcircle of
is tangent to the circumcircle of ![]() and
and ![]() is tangent to the circumcircle of the
is tangent to the circumcircle of the ![]() Therefore, we can use power of a point to solve for side ratios. We have
Therefore, we can use power of a point to solve for side ratios. We have ![]()
![]()
![]() Therefore,
Therefore, ![]() as
as ![]() and
and ![]() are cevians. Note that
are cevians. Note that ![]() lies on the circumcircle iff
lies on the circumcircle iff ![]() Substituting the values in, we have
Substituting the values in, we have ![]() so we are done.
so we are done. ![]()
Solution 6
Note that the givens immediately imply that ![]() , hence
, hence ![]() . Let
. Let ![]() be the midpoint of BC,
be the midpoint of BC, ![]() be the midpoint of
be the midpoint of ![]() , and
, and ![]() the midpoint of
the midpoint of ![]() . By the similar triangles, we have
. By the similar triangles, we have ![]() . We also have
. We also have ![]() , so we find
, so we find ![]() . We note that
. We note that ![]() , so
, so ![]() , which gives that
, which gives that ![]() and we are done.
and we are done.
As an addition, ![]() is the A-symmedian in
is the A-symmedian in ![]() .
.
Solution 7 (Pascal Theorem)
Let ![]() be the circumcircle of
be the circumcircle of ![]() . Let
. Let ![]() and
and ![]() be the intersection of
be the intersection of ![]() with
with ![]() and
and ![]() , respectively. By basic angle chasing, we have
, respectively. By basic angle chasing, we have ![]() and
and ![]() . So if the intersection of
. So if the intersection of ![]() and
and ![]() is
is ![]() ,
, ![]() bisects
bisects ![]() . And we know that
. And we know that ![]() bisects
bisects ![]() and
and ![]() , that means
, that means ![]() ,
, ![]() and
and ![]() are collinear. Now, we define the point
are collinear. Now, we define the point ![]() which is the intersection of
which is the intersection of ![]() and
and ![]() . And let us say
. And let us say ![]() to the intersection of
to the intersection of ![]() and
and ![]() . By Pascal Theorem at
. By Pascal Theorem at ![]() :
:
![]() ,
, ![]() and
and ![]() are collinear. That means
are collinear. That means ![]() is on
is on ![]() ,
, ![]() and
and ![]() . Therefore
. Therefore ![]() and this ends the proof because the intersection of
and this ends the proof because the intersection of ![]() and
and ![]() is the point
is the point ![]() which is on
which is on ![]() .
. ![]()
~Ege Saribas
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See Also
| 2014 IMO (Problems) • Resources | ||
| Preceded by Problem 3 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 5 |
| All IMO Problems and Solutions | ||