2016 USAMO Problems/Problem 5
Contents
[hide]Problem
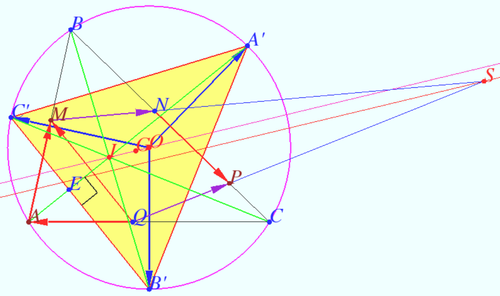
An equilateral pentagon ![]() is inscribed in triangle
is inscribed in triangle ![]() such that
such that ![]()
![]() and
and ![]() Let
Let ![]() be the intersection of lines
be the intersection of lines ![]() and
and ![]() Denote by
Denote by ![]() the angle bisector of
the angle bisector of ![]()
Prove that ![]() is parallel to
is parallel to ![]() where
where ![]() is the circumcenter of triangle
is the circumcenter of triangle ![]() and
and ![]() is the incenter of triangle
is the incenter of triangle ![]()
Solution 1
Let ![]() be the intersection of line
be the intersection of line ![]() and the circumcircle of
and the circumcircle of ![]() (other than
(other than ![]() ), then
), then ![]() . Let
. Let ![]() be the point such that
be the point such that ![]() is a rhombus. It follows that
is a rhombus. It follows that ![]() .
.
Since ![]() ,
, ![]() , or
, or ![]() . It follows that
. It follows that ![]() .
.
Since ![]() ,
, ![]() ,
, ![]() , it follows that
, it follows that ![]() , so
, so ![]() .
.
It is given that ![]() , and by basic properties of the incenter,
, and by basic properties of the incenter, ![]() . Therefore,
. Therefore, ![]() , so
, so ![]() .
Since the rotation between the two triangles in 90 degrees,
.
Since the rotation between the two triangles in 90 degrees, ![]() . However,
. However, ![]() is parallel to the bisector of
is parallel to the bisector of ![]() , which is perpendicular to
, which is perpendicular to ![]() , so we are done.
, so we are done.
Solution 2
Write ![]() for all
for all ![]() chosen as distinct vertices of triangle
chosen as distinct vertices of triangle ![]() . Define
. Define ![]() as sides opposite to angles
as sides opposite to angles ![]() , and
, and ![]() , respectively. Place the triangle in the Euclidean plane with
, respectively. Place the triangle in the Euclidean plane with ![]() at the origin and
at the origin and ![]() on the positive x-axis. Assume without loss of generality that C is acute.
on the positive x-axis. Assume without loss of generality that C is acute.
Consider the sides of the pentagon as vectors and note that ![]()
Define ![]() and
and ![]() as the angles made between the positive x-axis and
as the angles made between the positive x-axis and ![]() and
and ![]() , respectively. Considering the x and y coordinates of the vectors in
, respectively. Considering the x and y coordinates of the vectors in ![]() , it follows that
, it follows that
![]()
![]()
Suppose ![]() . Then
. Then ![]() , and the triangle is isosceles. In this case, it is clear by symmetry that
, and the triangle is isosceles. In this case, it is clear by symmetry that ![]() is vertical. Further, since point
is vertical. Further, since point ![]() exists,
exists, ![]() , so
, so ![]() and
and ![]() must be vertical as well.
must be vertical as well.
For the remainder of the proof, assume ![]() . Note that
. Note that ![]() whenever
whenever ![]() and
and ![]() . Note further that the slope of the line defined by the vector formed by summing vectors
. Note further that the slope of the line defined by the vector formed by summing vectors ![]() and
and ![]() is this expression. Since
is this expression. Since ![]() is parallel to
is parallel to ![]() , the slope of
, the slope of ![]() can be formed by dividing expressions in
can be formed by dividing expressions in ![]() and
and ![]() and inverting the sign:
and inverting the sign: ![]()
Determine the coordinates of ![]() by drawing perpendiculars from
by drawing perpendiculars from ![]() to the sides and vertices of the triangle. By exploiting congruence between pairs of right triangles that share a vertex, one can partition
to the sides and vertices of the triangle. By exploiting congruence between pairs of right triangles that share a vertex, one can partition ![]() into
into ![]() where
where ![]() are bases of these triangles that lie on the sides of triangle
are bases of these triangles that lie on the sides of triangle ![]() . From here it is clear that
. From here it is clear that ![]() .
.
To find the coordinates of ![]() , note that
, note that ![]() and that
and that ![]() in any acute triangle
in any acute triangle ![]() . It easily follows that
. It easily follows that ![]() . Note also that the perpendicular from
. Note also that the perpendicular from ![]() to
to ![]() bisects
bisects ![]() . Hence,
. Hence, ![]() if triangle
if triangle ![]() is acute.
is acute.
If triangle ![]() is obtuse at
is obtuse at ![]() , then it can be similarly shown that
, then it can be similarly shown that ![]() but that the remaining angles of this form are still
but that the remaining angles of this form are still ![]() and
and ![]() . It easily follows that
. It easily follows that ![]() holds if
holds if ![]() is obtuse. If
is obtuse. If ![]() is obtuse then
is obtuse then ![]() and the
and the ![]() coordinate of
coordinate of ![]() is
is ![]() . From this,
. From this, ![]() follows in this case as well.
follows in this case as well.
We can conclude the slope of ![]() is
is ![]() by the Law of Sines and rearrangement.
by the Law of Sines and rearrangement.
Setting ![]() is equivalent to
is equivalent to ![]()
Since ![]() , this equation is equivalent to
, this equation is equivalent to ![]()
This equation is equivalent to ![]() which is evident.
which is evident.
Solution 3
Let ![]() and
and ![]() be the arc midpoints of
be the arc midpoints of ![]() respectively. Let
respectively. Let ![]() be crosspoint of
be crosspoint of ![]() and
and ![]()
Therefore ![]() is the circumcenter of triangle
is the circumcenter of triangle ![]()
Points ![]() and
and ![]() are collinear.
are collinear.
![]()
![]() is orthocenter of
is orthocenter of ![]()
![]() is the Euler line of
is the Euler line of ![]()
Let ![]() be the centroid of
be the centroid of ![]() lies on line
lies on line ![]()
![]() is paraller to
is paraller to ![]()
![]()
Similarly ![]() rotation from
rotation from ![]() to
to ![]() , from
, from ![]() to
to ![]() and from
and from ![]() to
to ![]() is in clockwise direction,
is in clockwise direction, ![]()
![]() is perpendicular to
is perpendicular to ![]()
![]() therefore in accordance with Claim
therefore in accordance with Claim ![]() is parallel to
is parallel to ![]()
This sum is parallel to ![]() , so we are done.
, so we are done.
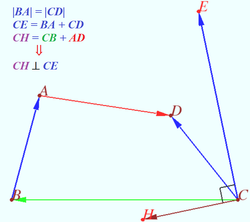
Claim
Let ![]() Then
Then ![]()
Proof
![]()
vladimir.shelomovskii@gmail.com, vvsss
Video Solution by MOP 2024
~r00tsOfUnity
See also
| 2016 USAMO (Problems • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()