2023 AIME I Problems/Problem 13

Problem

Each face of two noncongruent parallelepipeds is a rhombus whose diagonals have lengths $\sqrt{21}$ and $\sqrt{31}$ . The ratio of the volume of the larger of the two polyhedra to the volume of the smaller is $\frac{m}{n}$ , where $m$ and $n$ are relatively prime positive integers. Find $m + n$ . A parallelepiped is a solid with six parallelogram faces such as the one shown below.

$[asy] unitsize(2cm); pair o = (0, 0), u = (1, 0), v = 0.8*dir(40), w = dir(70); draw(o--u--(u+v)); draw(o--v--(u+v), dotted); draw(shift(w)*(o--u--(u+v)--v--cycle)); draw(o--w); draw(u--(u+w)); draw(v--(v+w), dotted); draw((u+v)--(u+v+w)); [/asy]$

Solution 1 (3-D Vector Analysis)

Denote $\alpha = \tan^{-1} \frac{\sqrt{21}}{\sqrt{31}}$ . Denote by $d$ the length of each side of a rhombus.

Now, we put the solid to the 3-d coordinate space. We put the bottom face on the $x-O-y$ plane. For this bottom face, we put a vertex with an acute angle $2 \alpha$ at the origin, denoted as $O$ . For two edges that are on the bottom face and meet at $O$ , we put one edge on the positive side of the $x$ -axis. The endpoint is denoted as $A$ . Hence, $A = \left( d , 0 , 0 \right)$ . We put the other edge in the first quadrant of the $x-O-y$ plane. The endpoint is denoted as $B$ . Hence, $B = \left( d \cos 2 \alpha , d \sin 2 \alpha , 0 \right)$ .

For the third edge that has one endpoint $O$ , we denote by $C$ its second endpoint. We denote $C = \left( u , v , w \right)$ . Without loss of generality, we set $w > 0$ . Hence, $u^2 + v^2 + w^2 = d^2 . \hspace{1cm} (1)$

We have $\begin{align*} \cos \angle AOC & = \frac{\overrightarrow{OA} \cdot \overrightarrow{OC}}{|OA| \cdot |OC|} \\ & = \frac{u}{d} , \hspace{1cm} (2) \end{align*}$ and $\begin{align*} \cos \angle BOC & = \frac{\overrightarrow{OB} \cdot \overrightarrow{OC}}{|OB| \cdot |OC|} \\ & = \frac{u \cos 2 \alpha + v \sin 2 \alpha}{d} . \hspace{1cm} (3) \end{align*}$

Case 1: $\angle AOC = \angle BOC = 2 \alpha$ or $2 \left( 90^\circ - \alpha \right)$ .

By solving (2) and (3), we get $\begin{align*} u & = \pm d \cos 2 \alpha , \\ v & = \pm d \cos 2 \alpha \frac{1 - \cos 2 \alpha}{\sin 2 \alpha} \\ & = \pm d \cos 2 \alpha \tan \alpha . \end{align*}$

Plugging these into (1), we get $\begin{align*} w & = d \sqrt{1 - \cos^2 2 \alpha - \cos^2 2 \alpha \tan^2 \alpha} \\ & = d \sqrt{\sin^2 2 \alpha - \cos^2 2 \alpha \tan^2 \alpha} . \hspace{1cm} (4) \end{align*}$

Case 2: $\angle AOC = 2 \alpha$ and $\angle BOC = 2 \left( 90^\circ - \alpha \right)$ , or $\angle BOC = 2 \alpha$ and $\angle AOC = 2 \left( 90^\circ - \alpha \right)$ .

By solving (2) and (3), we get $\begin{align*} u & = \pm d \cos 2 \alpha , \\ v & = \mp d \cos 2 \alpha \frac{1 + \cos 2 \alpha}{\sin 2 \alpha} \\ & = \mp d \cos 2 \alpha \cot \alpha . \end{align*}$

Plugging these into (1), we get $\begin{align*} w & = d \sqrt{1 - \cos^2 2 \alpha - \cos^2 2 \alpha \cot^2 \alpha} \\ & = d \sqrt{\sin^2 2 \alpha - \cos^2 2 \alpha \cot^2 \alpha} . \hspace{1cm} (5) \end{align*}$

We notice that $(4) > (5)$ . Thus, (4) (resp. (5)) is the parallelepiped with a larger (resp. smaller) height.

Therefore, the ratio of the volume of the larger parallelepiped to the smaller one is $\begin{align*} \frac{(4)}{(5)} & = \frac{\sqrt{\sin^2 2 \alpha - \cos^2 2 \alpha \tan^2 \alpha}} {\sqrt{\sin^2 2 \alpha - \cos^2 2 \alpha \cot^2 \alpha}} \\ & = \sqrt{\frac{\tan^2 2 \alpha - \tan^2 \alpha}{\tan^2 2 \alpha - \cot^2 \alpha}} . \end{align*}$

Recall that $\tan \alpha = \frac{\sqrt{21}}{\sqrt{31}}$ . Thus, $\tan 2 \alpha = \frac{2 \tan \alpha}{1 - \tan^2 \alpha} = \frac{\sqrt{21 \cdot 31}}{5}$ . Plugging this into the equation above, we get $\begin{align*} \frac{(4)}{(5)} & = \frac{63}{62}. \end{align*}$

Therefore, the answer is $63 + 62 = \boxed{\textbf{(125) }}$ .

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 2 (no trig)

Let one of the vertices be at the origin and the three adjacent vertices be $u$ , $v$ , and $w$ . For one of the parallelepipeds, the three diagonals involving the origin have length $\sqrt {21}$ . Hence, $(u+v)\cdot (u+v)=u\cdot u+v\cdot v+2u\cdot v=21$ and $(u-v)\cdot (u-v)=u\cdot u+v\cdot v-2u\cdot v=31$ . Since all of $u$ , $v$ , and $w$ have equal length, $u\cdot u=13$ , $v\cdot v=13$ , and $u\cdot v=-2.5$ . Symmetrically, $w\cdot w=13$ , $u\cdot w=-2.5$ , and $v\cdot w=-2.5$ . Hence the volume of the parallelepiped is given by $\sqrt{\operatorname{det}\begin{pmatrix}13&-2.5&-2.5\\-2.5&13&-2.5\\-2.5&-2.5&13\end{pmatrix}}=\sqrt{\operatorname{det}\begin{pmatrix}15.5&-15.5&0\\-2.5&13&-2.5\\0&-15.5&15.5\end{pmatrix}}=\sqrt{15.5^2\operatorname\det\begin{pmatrix}1&-1&0\\-2.5&13&-2.5\\0&-1&1\end{pmatrix}}=\sqrt{15.5^2\cdot 8}$ .

For the other parallelepiped, the three diagonals involving the origin are of length $\sqrt{31}$ and the volume is $\sqrt{\operatorname{det}\begin{pmatrix}13&2.5&2.5\\2.5&13&2.5\\2.5&2.5&13\end{pmatrix}}=\sqrt{\operatorname{det}\begin{pmatrix}10.5&-10.5&0\\2.5&13&2.5\\0&-10.5&10.5\end{pmatrix}}=\sqrt{10.5^2\operatorname\det\begin{pmatrix}1&-1&0\\2.5&13&2.5\\0&-1&1\end{pmatrix}}=\sqrt{10.5^2\cdot 18}$ .

Consequently, the answer is $\sqrt\frac{10.5^2\cdot 18}{15.5^2\cdot 8}=\frac{63}{62}$ , giving $\boxed{125}$ .

~EVIN-

Solution 3 (No trig, no linear algebra)

Observe that both parallelepipeds have two vertices (one on each base) that have three congruent angles meeting at them. Denote the parallelepiped with three acute angles meeting $P$ , and the one with three obtuse angles meeting $P'$ .

The area of a parallelepiped is simply the base area times the height, but because both parallelepipeds have the same base, what we want is just the ratio of the heights.

Denote the point with three acute angles meeting at it in $P$ as $A$ , and its neighbors $B$ , $C$ , and $D$ . Similarly, denote the point with three obtuse angles meeting at it in $P'$ as $A'$ , and its neighbors $B'$ , $C'$ , and $D'$ .

We have the following equations:

$\textrm{Height of }P\textrm{ from }ACD = \frac{\textrm{Vol}(ABCD) \cdot 3}{[ACD]},$ $\textrm{Height of }P'\textrm{ from }A'C'D' = \frac{\textrm{Vol}(A'B'C'D') \cdot 3}{[A'C'D']}.$

However, $ACD$ and $A'C'D'$ are both half the area of a rhombus with diagonals $\sqrt{31}$ and $\sqrt{21}$ , so our ratio is really

$\frac{P}{P'} = \frac{\textrm{Vol}(ABCD)}{\textrm{Vol}(A'B'C'D')}.$

Because the diagonals of all of the faces are $\sqrt{31}$ and $\sqrt{21}$ , each edge of the parallelepipeds is $\sqrt{13}$ by the Pythagorean theorem.

We have $AB = AC = AD = \sqrt{13}$ , and $BC = CD = BD = \sqrt{21}$ . When we drop a perpendicular to the centroid of $BCD$ from $A$ (let's call this point $O$ ), we have $BO = \frac{\sqrt{21}}{\sqrt{3}} = \sqrt{7}$ . Thus,

$AB^2 - BO^2 = AO^2$ $13 - 7 = AO^2 = 6$ $AO = \sqrt{6}.$

The area of base $BCD$ is $\frac{21\sqrt{3}}{4}$ . Hence,

$\textrm{Vol}(ABCD) = \frac{\sqrt{6}\cdot\frac{21\sqrt{3}}{4}}{3}$ $= \frac{63\sqrt{2}}{12}.$

We can apply a similar approach to $A'B'C'D'$ .

$A'B' = A'C' = A'D' = \sqrt{13}$ , and $B'C' = C'D' = B'D' = \sqrt{31}$ . When we drop a perpendicular to the centroid of $B'C'D'$ from $A'$ (let's call this point $O'$ ), we have $B'O' = \frac{\sqrt{31}}{\sqrt{3}} = \sqrt{\frac{31}{3}}$ . Thus,

$A'B'^2 - B'O'^2 = A'O'^2$ $13 - \frac{31}{3} = A'O'^2$ $A'O' = \sqrt{8}{3} = \frac{2\sqrt{6}}{3}.$

The area of base $B'C'D'$ is $\frac{31\sqrt{3}}{4}$ . Hence,

$\textrm{Vol}(A'B'C'D') = \frac{\frac{2\sqrt{6}}{3}\cdot\frac{31\sqrt{3}}{4}}{3}$ $= \frac{186\sqrt{2}}{36}$ $= \frac{62\sqrt{2}}{12}.$

Finally,

$\frac{P}{P'} = \frac{\textrm{Vol}(ABCD)}{\textrm{Vol}(A'B'C'D')} = \frac{\frac{63\sqrt{2}}{12}}{\frac{62\sqrt{2}}{12}} = \frac{63}{62}.$

Our answer is $63 + 62 = \boxed{125}$ .

~mathboy100

Solution 4 (Pythagorean theorem)

Since the two parallelepipeds have the same base, all we need to do is to find their respective heights.

$[asy] unitsize(2cm); pair a = (0, 0), b = (1, 0), c = 0.8*dir(40), d = dir(70), p = 0.33*dir(20), o = (b+c)/2; label("A",a,S); label("B",b,S); label("C",c,S); label("D",d,N); label("P",p,S); label("O",o,E); draw(a--b--(b+c)); draw(a--c--(b+c), dotted); draw(shift(d)*(a--b--(b+c)--c--cycle)); draw(a--d); draw(b--(b+d)); draw(c--(c+d), dotted); draw((b+c)--(b+c+d)); draw(d--p, dotted); draw(c--b, dotted); draw(a--(b+c), dotted); draw(p--c, dotted); draw(d--c, dotted); [/asy]$

As illustrated in the above diagram, drop a perpendicular from $D$ onto the base at $P$ . Denote the center of the base by $O$ . By symmetry, $P$ must be on $AO$ . Now we need to find $DP$ .

Apply Pythagorean theorem to $\triangle DPA$ we have $DP^2 = AD^2 - AP^2.$

Apply Pythagorean theorem to $\triangle DPC$ and then $\triangle CPO$ we have $DP^2 = DC^2 - CP^2 = DC^2 - (CO^2 + OP^2) = DC^2 - (CO^2 + (AO-AP)^2) = DC^2 - CO^2 - (AO-AP)^2.$

Combining the above two, we have $AD^2 - AP^2 = DC^2 - CO^2 - (AO-AP)^2.$

Since $AD=\sqrt{13}$ , $DC=\sqrt{21}$ , $CO=\frac{\sqrt{21}}{2}$ , $AO=\frac{\sqrt{31}}{2}$ , plug them into the above equation and solve for the only unknown variable $AP$ , we get $AP=\frac{5}{\sqrt{31}}.$

Thus the height $DP = \sqrt{AD^2 - AP^2} = \sqrt{13 - \frac{25}{31}} = \sqrt{\frac{378}{31}}.$

$[asy] unitsize(2cm); pair a = (0, 0), b = (1, 0), c = 0.8*dir(40), d = 0.7*dir(80), e = c+d, p = 0.9*dir(10), o = (b+c)/2; label("A'",a,S); label("B'",b,S); label("C'",c,W); label("E'",e,N); label("P'",p,S); label("O'",o,W); draw(a--b--(b+c)); draw(a--c--(b+c), dotted); draw(shift(d)*(a--b--(b+c)--c--cycle)); draw(a--d); draw(b--(b+d)); draw(c--(c+d), dotted); draw((b+c)--(b+c+d)); draw(e--p, dotted); draw(c--b, dotted); draw(a--(b+c), dotted); draw(p--a, dotted); draw(e--a, dotted); [/asy]$

For the other parallelepiped, using the same approach and drop a perpendicular from $E'$ onto the base at $P'$ . Similarly applying Pythagorean theorem to $\triangle E'P'C'$ , $\triangle E'P'A'$ and $\triangle A'P'O'$ we have $C'E'^2 - C'P'^2 = A'E'^2 - A'O'^2 - (C'P'-C'O')^2.$

Plugging known values into the above equation and solve for the only unknown variable $C'P'$ , we get $C'P'=\frac{5}{\sqrt{21}}.$

Thus the height $E'P' = \sqrt{C'E'^2 - C'P'^2} = \sqrt{13 - \frac{25}{21}} = \sqrt{\frac{248}{21}}.$

The ratio between the two is therefore $\frac{DP}{E'P'} = \frac{\sqrt{\frac{378}{31}}}{\sqrt{\frac{248}{21}}} = \sqrt{\frac{2\cdot3^3\cdot7}{31}\cdot\frac{3\cdot7}{2^3\cdot31}} = \frac{3^2\cdot7}{2\cdot31} = \frac{63}{62}$ , giving $\boxed{125}$ .

~sgdzw

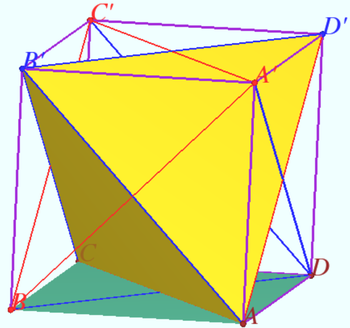
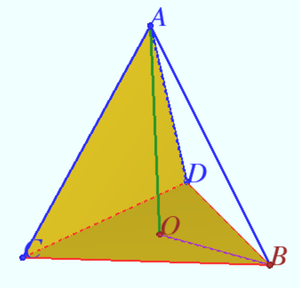
Solution 5 (Visual)

Let us inscribe a tetrahedron $ACB'D'$ in given parallelepiped so that its edges coincide with the diagonals of the faces of the parallelepiped. Note that the three edges outgoing from the vertex $B'$ have the same length $b$ , and the three edges at the base have a different length $a.$

The volume of the tetrahedron $V= \frac {a^2}{12}\sqrt{3b^2 - a^2}$ is three times less than the volume of the parallelepiped.

In second parallelepiped $a$ and $b$ change the positions.

Required ratio is $\frac {a^2 \cdot \sqrt {3b^2 - a^2}}{b^2 \cdot \sqrt {3a^2 - b^2}} = \frac {21 \sqrt {3 \cdot 31 - 21}}{31 \cdot \sqrt{3 \cdot 21 - 31}} = \frac {21 \sqrt {72}}{31 \sqrt {32}}= \frac {63}{62}.$

Claim

Let $ABCD$ be the regular pyramid, $AB = AC = AD = b, BC = BD = CD = a.$

The area of $\triangle BCD = \frac {a^2 \sqrt {3}}{4}.$

Height $AO^2 = AB^2 - OB^2 = {b^2 - \frac {a^2}{3}}.$

Volume $V= \frac {a^2}{12}\sqrt{3b^2 - a^2}.$

vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtu.be/5mJ6EqdFD94

~MathProblemSolvingSkills.com

Animated Video Solution

https://youtu.be/VvCl5KIqT9M

~Star League (https://starleague.us)

2023 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.

Page

Toolbox

Search