2023 AIME I Problems/Problem 8
Contents
[hide]Problem
Rhombus ![]() has
has ![]() There is a point
There is a point ![]() on the incircle of the rhombus such that the distances from
on the incircle of the rhombus such that the distances from ![]() to the lines
to the lines ![]() and
and ![]() are
are ![]()
![]() and
and ![]() respectively. Find the perimeter of
respectively. Find the perimeter of ![]()
Diagram
![[asy] /* Made by MRENTHUSIASM; inspired by Math Jams. */ size(300); pair A, B, C, D, O, P, R, S, T; A = origin; B = (125/4,0); C = B + 125/4 * dir((3,4)); D = A + 125/4 * dir((3,4)); O = (25,25/2); P = (15,5); R = foot(P,A,D); S = foot(P,A,B); T = foot(P,B,C); markscalefactor=0.15; draw(rightanglemark(P,R,D)^^rightanglemark(P,S,B)^^rightanglemark(P,T,C),red); draw(Circle(O,25/2)^^A--B--C--D--cycle^^B--T); draw(P--R^^P--S^^P--T,red+dashed); dot("$A$",A,1.5*dir(225),linewidth(4.5)); dot("$B$",B,1.5*dir(-45),linewidth(4.5)); dot("$C$",C,1.5*dir(45),linewidth(4.5)); dot("$D$",D,1.5*dir(135),linewidth(4.5)); dot("$P$",P,1.5*dir(60),linewidth(4.5)); dot(R^^S^^T,linewidth(4.5)); dot(O,linewidth(4.5)); label("$9$",midpoint(P--R),dir(A-D),red); label("$5$",midpoint(P--S),dir(180),red); label("$16$",midpoint(P--T),dir(A-D),red); [/asy]](http://latex.artofproblemsolving.com/7/a/4/7a46c819299929a4aeb5ab4655da9ef0db9e650a.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1
This solution refers to the Diagram section.
Let ![]() be the incenter of
be the incenter of ![]() for which
for which ![]() is tangent to
is tangent to ![]() and
and ![]() at
at ![]() and
and ![]() respectively. Moreover, suppose that
respectively. Moreover, suppose that ![]() and
and ![]() are the feet of the perpendiculars from
are the feet of the perpendiculars from ![]() to
to ![]() and
and ![]() respectively, such that
respectively, such that ![]() intersects
intersects ![]() at
at ![]() and
and ![]()
We obtain the following diagram:
![[asy] /* Made by MRENTHUSIASM; inspired by Math Jams. */ size(300); pair A, B, C, D, O, P, R, S, T, X, Y, Z, Q; A = origin; B = (125/4,0); C = B + 125/4 * dir((3,4)); D = A + 125/4 * dir((3,4)); O = (25,25/2); P = (15,5); R = foot(P,A,D); S = foot(P,A,B); T = foot(P,B,C); X = (15,20); Y = (25,0); Z = (35,5); Q = intersectionpoints(Circle(O,25/2),R--T)[1]; fill(R--T--Z--X--cycle,cyan); markscalefactor=0.15; draw(rightanglemark(P,R,D)^^rightanglemark(P,S,B)^^rightanglemark(P,T,C),red); draw(Circle(O,25/2)^^A--B--C--D--cycle^^B--T); draw(P--R^^P--S^^P--T,red+dashed); draw(O--X^^O--Y^^O--Z); dot("$A$",A,1.5*dir(225),linewidth(4.5)); dot("$B$",B,1.5*dir(-45),linewidth(4.5)); dot("$C$",C,1.5*dir(45),linewidth(4.5)); dot("$D$",D,1.5*dir(135),linewidth(4.5)); dot("$P$",P,1.5*dir(60),linewidth(4.5)); dot("$R$",R,1.5*dir(135),linewidth(4.5)); dot("$S$",S,1.5*dir(-90),linewidth(4.5)); dot("$T$",T,1.5*dir(-45),linewidth(4.5)); dot("$O$",O,1.5*dir(45),linewidth(4.5)); dot("$X$",X,1.5*dir(135),linewidth(4.5)); dot("$Y$",Y,1.5*dir(-90),linewidth(4.5)); dot("$Z$",Z,1.5*dir(-45),linewidth(4.5)); dot("$Q$",Q,1.5*dir(60),linewidth(4.5)); label("$9$",midpoint(P--R),dir(A-D),red); label("$5$",midpoint(P--S),dir(180),red); label("$16$",midpoint(P--T),dir(A-D),red); [/asy]](http://latex.artofproblemsolving.com/6/0/e/60e267254e4ca46ec47c5d5313637e5a710ec7a4.png) Note that
Note that ![]() by the properties of tangents, so
by the properties of tangents, so ![]() is a rectangle. It follows that the diameter of
is a rectangle. It follows that the diameter of ![]() is
is ![]()
Let ![]() and
and ![]() We apply the Power of a Point Theorem to
We apply the Power of a Point Theorem to ![]() and
and ![]()
![]() We solve this system of equations to get
We solve this system of equations to get ![]() and
and ![]() Alternatively, we can find these results by the symmetry on rectangle
Alternatively, we can find these results by the symmetry on rectangle ![]() and semicircle
and semicircle ![]()
We extend ![]() beyond
beyond ![]() to intersect
to intersect ![]() and
and ![]() at
at ![]() and
and ![]() respectively, where
respectively, where ![]() So, we have
So, we have ![]() and
and ![]() On the other hand, we have
On the other hand, we have ![]() by the Pythagorean Theorem on right
by the Pythagorean Theorem on right ![]() Together, we conclude that
Together, we conclude that ![]() Therefore, points
Therefore, points ![]() and
and ![]() must be collinear.
must be collinear.
Let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() Note that
Note that ![]() as shown below:
as shown below:
![[asy] /* Made by MRENTHUSIASM; inspired by Math Jams. */ size(300); pair A, B, C, D, O, P, R, S, T, X, Y, Z, Q, G; A = origin; B = (125/4,0); C = B + 125/4 * dir((3,4)); D = A + 125/4 * dir((3,4)); O = (25,25/2); P = (15,5); R = foot(P,A,D); S = foot(P,A,B); T = foot(P,B,C); X = (15,20); Y = (25,0); Z = (35,5); Q = intersectionpoints(Circle(O,25/2),R--T)[1]; G = foot(D,A,B); fill(D--A--G--cycle,green); fill(P--R--X--cycle,yellow); markscalefactor=0.15; draw(rightanglemark(P,R,D)^^rightanglemark(D,G,A),red); draw(Circle(O,25/2)^^A--B--C--D--cycle^^X--P^^D--G); draw(P--R,red+dashed); dot("$A$",A,1.5*dir(225),linewidth(4.5)); dot("$B$",B,1.5*dir(-45),linewidth(4.5)); dot("$C$",C,1.5*dir(45),linewidth(4.5)); dot("$D$",D,1.5*dir(135),linewidth(4.5)); dot("$P$",P,1.5*dir(60),linewidth(4.5)); dot("$R$",R,1.5*dir(135),linewidth(4.5)); dot("$O$",O,1.5*dir(45),linewidth(4.5)); dot("$X$",X,1.5*dir(135),linewidth(4.5)); dot("$G$",G,1.5*dir(-90),linewidth(4.5)); draw(P--X,MidArrow(0.3cm,Fill(red))); draw(G--D,MidArrow(0.3cm,Fill(red))); label("$9$",midpoint(P--R),dir(A-D),red); label("$12$",midpoint(R--X),dir(135),red); label("$15$",midpoint(X--P),dir(0),red); label("$25$",midpoint(G--D),dir(0),red); [/asy]](http://latex.artofproblemsolving.com/e/f/f/effba087a5a47768baa7c189da8bfab7458a64e7.png) As
As ![]() and
and ![]() we conclude that
we conclude that ![]() by the AA Similarity. The ratio of similitude is
by the AA Similarity. The ratio of similitude is ![]() We get
We get ![]() from which
from which ![]()
Finally, the perimeter of ![]() is
is ![]()
~MRENTHUSIASM (inspired by awesomeming327. and WestSuburb)
Solution 2
Let ![]() be the extension of line
be the extension of line ![]() such that
such that ![]()
![]() be the point where
be the point where ![]() is tangent to the circle,
is tangent to the circle, ![]() be where the perpendicular from
be where the perpendicular from ![]() to line
to line ![]() meets the circle after point
meets the circle after point ![]() , and
, and ![]() be the point where
be the point where ![]() meets
meets ![]() (point
(point ![]() is added to make it clear that
is added to make it clear that ![]() is not on
is not on ![]() ).
).
Connect ![]() to the point where the circle is tangent to
to the point where the circle is tangent to ![]() , call this point
, call this point ![]() Since
Since ![]() is a diameter,
is a diameter, ![]() is a chord, and
is a chord, and ![]() the perpendicular bisector of
the perpendicular bisector of ![]() will also perpendicularly bisect
will also perpendicularly bisect ![]() So trapezoid
So trapezoid ![]() is symmetrical about this perpendicular bisector and is therefore isosceles. Then
is symmetrical about this perpendicular bisector and is therefore isosceles. Then ![]() So by Leg-Leg congruence
So by Leg-Leg congruence ![]() Then
Then ![]() and since the length of
and since the length of ![]() is
is ![]()
![]() Now, consider the right triangle formed by the radius, height, and half of the top base of the isosceles trapezoid. Let
Now, consider the right triangle formed by the radius, height, and half of the top base of the isosceles trapezoid. Let ![]() be the height. We have
be the height. We have ![]() Then by the Pythagorean Theorem on
Then by the Pythagorean Theorem on ![]() ,
, ![]()
We observe that ![]() since right triangles
since right triangles ![]() and
and ![]() share common angle
share common angle ![]()
Therefore, ![]() .
.
The height of the rhombus is ![]() . If
. If ![]() is the side length of the rhombus,
is the side length of the rhombus, ![]() is the height, and
is the height, and ![]() is an interior angle, then
is an interior angle, then ![]() (you can see this by dropping an altitude from
(you can see this by dropping an altitude from ![]() to
to ![]() ).
).
Given ![]() , we have
, we have ![]() .
.
Solving, we find ![]() .
.
So the perimeter of the rhombus is ![]() .
.
Solution 3
This solution refers to the Diagram section.
Define points ![]() and
and ![]() as Solution 1 does. Moreover, let
as Solution 1 does. Moreover, let
![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]()
![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() and
and
![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]()
We obtain the following diagram:
![[asy] /* Made by MRENTHUSIASM; inspired by Math Jams. */ size(300); pair A, B, C, D, O, P, R, S, T, H, M, N; A = origin; B = (125/4,0); C = B + 125/4 * dir((3,4)); D = A + 125/4 * dir((3,4)); O = (25,25/2); P = (15,5); R = foot(P,A,D); S = foot(P,A,B); T = foot(P,B,C); H = foot(S,C,D); M = foot(O,S,H); N = foot(O,R,T); fill(O--M--P--cycle,yellow); fill(O--N--P--cycle,green); markscalefactor=0.15; draw(rightanglemark(P,R,D)^^rightanglemark(P,S,B)^^rightanglemark(P,T,C)^^rightanglemark(O,M,P)^^rightanglemark(O,N,P)^^rightanglemark(S,H,D),red); draw(Circle(O,25/2)^^A--B--C--D--cycle^^B--T^^D--H^^O--M^^O--N^^O--P); draw(P--R^^P--S^^P--T^^P--H,red+dashed); dot("$A$",A,1.5*dir(225),linewidth(4.5)); dot("$B$",B,1.5*dir(-45),linewidth(4.5)); dot("$C$",C,1.5*dir(45),linewidth(4.5)); dot("$D$",D,1.5*dir(90),linewidth(4.5)); dot("$P$",P,1.5*dir(60),linewidth(4.5)); dot("$R$",R,1.5*dir(135),linewidth(4.5)); dot("$S$",S,1.5*dir(-90),linewidth(4.5)); dot("$T$",T,1.5*dir(-45),linewidth(4.5)); dot("$O$",O,1.5*dir(45),linewidth(4.5)); dot("$H$",H,1.5*dir(90),linewidth(4.5)); dot("$M$",M,1.5*dir(180),linewidth(4.5)); dot("$N$",N,1.5*dir(15),linewidth(4.5)); label("$9$",midpoint(P--R),dir(A-D),red); label("$5$",midpoint(P--S),dir(180),red); label("$16$",midpoint(P--T),dir(A-D),red); [/asy]](http://latex.artofproblemsolving.com/d/9/2/d92da4498a9eafd5d7d49595514b87d6522d1a15.png) Note that the diameter of
Note that the diameter of ![]() is
is ![]() so
so ![]() It follows that:
It follows that:
- In right
 we have
we have  by symmetry, from which
by symmetry, from which  by the Pythagorean Theorem.
by the Pythagorean Theorem. - In right
 we have
we have  by symmetry, from which
by symmetry, from which  by the Pythagorean Theorem.
by the Pythagorean Theorem.
Since ![]() and
and ![]() we conclude that
we conclude that ![]() We apply the Sine of a Sum Formula:
We apply the Sine of a Sum Formula:
 Note that
Note that ![]() from which
from which ![]() We solve this equation to get
We solve this equation to get ![]()
Finally, the perimeter of ![]() is
is ![]()
~MRENTHUSIASM (credit given to TheAMCHub)
Solution 4
Label the points of the rhombus to be ![]() ,
, ![]() ,
, ![]() , and
, and ![]() and the center of the incircle to be
and the center of the incircle to be ![]() so that
so that ![]() ,
, ![]() , and
, and ![]() are the distances from point
are the distances from point ![]() to side
to side ![]() , side
, side ![]() , and
, and ![]() respectively. Through this, we know that the distance from the two pairs of opposite lines of rhombus
respectively. Through this, we know that the distance from the two pairs of opposite lines of rhombus ![]() is
is ![]() and circle
and circle ![]() has radius
has radius ![]() .
.
Call the feet of the altitudes from ![]() to side
to side ![]() , side
, side ![]() , and side
, and side ![]() to be
to be ![]() ,
, ![]() , and
, and ![]() respectively. Additionally, call the feet of the altitudes from
respectively. Additionally, call the feet of the altitudes from ![]() to side
to side ![]() , side
, side ![]() , and side
, and side ![]() to be
to be ![]() ,
, ![]() , and
, and ![]() respectively.
respectively.
Draw a line segment from ![]() to
to ![]() so that it is perpendicular to
so that it is perpendicular to ![]() . Notice that this segment length is equal to
. Notice that this segment length is equal to ![]() and is
and is  by Pythagorean Theorem.
by Pythagorean Theorem.
Similarly, perform the same operations with perpendicular from ![]() to
to ![]() to get
to get ![]() .
.
By equal tangents, ![]() . Now, label the length of segment
. Now, label the length of segment ![]() and
and ![]() .
.
Using Pythagorean Theorem again, we get

Which also gives us ![]() and
and ![]() .
.
Since the diagonals of the rhombus intersect at ![]() and are angle bisectors and are also perpendicular to each other, we can get that
and are angle bisectors and are also perpendicular to each other, we can get that

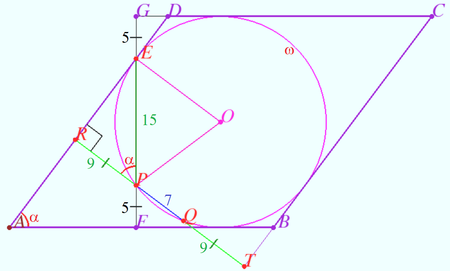
Solution 5
Denote by ![]() the center of
the center of ![]() .
We drop an altitude from
.
We drop an altitude from ![]() to
to ![]() that meets
that meets ![]() at point
at point ![]() .
We drop altitudes from
.
We drop altitudes from ![]() to
to ![]() and
and ![]() that meet
that meet ![]() and
and ![]() at
at ![]() and
and ![]() , respectively.
We denote
, respectively.
We denote ![]() .
We denote the side length of
.
We denote the side length of ![]() as
as ![]() .
.
Because the distances from ![]() to
to ![]() and
and ![]() are
are ![]() and
and ![]() , respectively, and
, respectively, and ![]() , the distance between each pair of two parallel sides of
, the distance between each pair of two parallel sides of ![]() is
is ![]() .
Thus,
.
Thus, ![]() and
and ![]() .
.
We have

Thus, ![]() .
.
In ![]() , we have
, we have ![]() .
Thus,
.
Thus,
![]()
Taking the imaginary part of this equation and plugging ![]() and
and ![]() into this equation, we get
into this equation, we get
![]()
We have

Because ![]() is on the incircle of
is on the incircle of ![]() ,
, ![]() . Plugging this into
. Plugging this into ![]() , we get the following equation
, we get the following equation
![]()
By solving this equation, we get ![]() and
and ![]() .
Therefore,
.
Therefore, ![]() .
.
Therefore, the perimeter of ![]() is
is ![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 6
The center of the incircle is ![]() Denote the points in which the incircle meets
Denote the points in which the incircle meets ![]()
![]()
![]() and
and ![]() as
as ![]()
![]()
![]() and
and ![]() respectively. Next, also denote the base of the perpendicular from
respectively. Next, also denote the base of the perpendicular from ![]() to
to ![]()
![]()
![]() and
and ![]() as
as ![]()
![]()
![]() and
and ![]() respectively.
respectively.
We can easily see that the radius of the circle is ![]() Using this and Pythagorus on right
Using this and Pythagorus on right ![]() and
and ![]() we find that
we find that ![]() and
and ![]()
Since ![]() by properties of circle tangents, we can deduce by the above information that
by properties of circle tangents, we can deduce by the above information that ![]() Doing Pythagorus on right
Doing Pythagorus on right ![]() and
and ![]() we find that
we find that ![]() (because
(because ![]() ) From solving the
) From solving the ![]() just derived equations, we find that
just derived equations, we find that ![]() and
and ![]()
Next, we use Pythagorus on right ![]() (we can see it's right because of properties of rhombuses.) We get
(we can see it's right because of properties of rhombuses.) We get ![]() We know
We know ![]() By Pythagorus on
By Pythagorus on ![]() and
and ![]() we also know
we also know ![]() and
and ![]() Substituting these in, we have
Substituting these in, we have ![]() Solving for
Solving for ![]() we get
we get ![]() Now we find that each side of the rhombus
Now we find that each side of the rhombus ![]() The perimeter of the rhombus would be that times
The perimeter of the rhombus would be that times ![]() Our final answer is
Our final answer is ![]()
~s214425
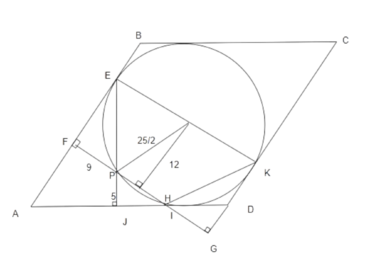
Solution 7
Notation is shown on diagram, ![]()
![]() as hights of rhombus.
as hights of rhombus.
![]()
![]()
![]()
![]() The perimeter of
The perimeter of ![]() is
is ![]()
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
~MathProblemSolvingSkills.com
See also
| 2023 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()