2023 AMC 10B Problems/Problem 22

1 Problem
2 Solution 1
3 Solution 2 (Desperate)
4 Solution 3 (Three Cases)
5 Solution 4
6 Solution 5
7 Solution 6 (Quick)
8 Solution 7
9 Solution 8
10 Solution 9 (Very Fast)
11 Solution 10(has 3 cases)
12 Solution 11 (Based on graph)
13 Video Solution 1 by OmegaLearn
14 Video Solution 2 by SpreadTheMathLove
15 Video Solution
16 See also

Problem

How many distinct values of $x$ satisfy $\lfloor{x}\rfloor^2-3x+2=0$ , where $\lfloor{x}\rfloor$ denotes the largest integer less than or equal to $x$ ?

$\textbf{(A) } \text{an infinite number} \qquad \textbf{(B) } 4 \qquad \textbf{(C) } 2 \qquad \textbf{(D) } 3 \qquad \textbf{(E) } 0$

Solution 1

To further grasp at this equation, we rearrange the equation into $\lfloor{x}\rfloor^2=3x-2.$ Thus, $3x-2$ is a perfect square and nonnegative. It is now much more apparent that $x \ge 2/3,$ and that $x = 2/3$ is a solution.

Additionally, by observing the RHS, $x<4,$ as $\lfloor{4}\rfloor^2 > 3\cdot4,$ since squares grow quicker than linear functions.

Now that we have narrowed down our search, we can simply test for intervals $[2/3,1], [1,2],[2,3],[3,4).$ This intuition to use intervals stems from the fact that $x=1,2$ are observable integral solutions.

Notice how there is only one solution per interval, as $3x-2$ increases while $\lfloor{x}\rfloor^2$ stays the same.

Finally, we see that $x=3$ does not work, however, through setting $\lfloor{x}\rfloor^2 = 9,$ $x = 11/3$ is a solution and within our domain of $[3,4).$

This provides us with solutions $\left(\frac23, 1, 2, \frac{11}{3}\right),$ thus the final answer is $\boxed{(\text{B}) \ 4}.$

~mathbrek, happyhari

Solution 2 (Desperate)

Notice there has to be a solution for $x$ between $(2,-3)$ and $(1,2)$ because of the floors. There is also no way $2$ solutions because of the quadratic, and when we add them together, we get $\boxed{(\text{B}) \ 4}.$ ~perion.

Solution 3 (Three Cases)

First, let's take care of the integer case--clearly, only $x=1,2$ work. Then, we know that $3x$ must be an integer. Set $x=\frac{a}3$ . Now, there are two cases for the value of $\lfloor x\rfloor$ . Case 1: $\lfloor x\rfloor=\frac{a-1}{3}$ $\frac{a^2-2a+1}{9}=a-2\rightarrow a^2-2a+1=9a-18\rightarrow a^2-11a+19=0.$ There are no solutions in this case. Case 2: $\lfloor x\rfloor=\frac{a-2}{3}$ $\frac{a^2-4a+4}{9}=a-2\rightarrow a^2-4a+4=9a-18\rightarrow a^2-13a+22=0.$ This case provides the two solutions $\frac23$ and $\frac{11}3$ as two more solutions. Our final answer is thus $\boxed{4}$ .

~wuwang2002

Solution 4

First, $x=2,1$ are trivial solutions

We assume from the shape of a parabola and the nature of the floor function that any additional roots will be near 2 and 1

We can now test values for $\lfloor{x}\rfloor$ :

$\lfloor{x}\rfloor=0$

We have $0-3x+2=0$ . Solving, we have $x=\frac{2}{3}$ . We see that $\lfloor{\frac{2}{3}}\rfloor=0$ , so this solution is valid

$\lfloor{x}\rfloor=-1$

We have $1-3x+2=0$ . Solving, we have $x=1$ . $\lfloor{1}\rfloor\neq-1$ , so this is not valid. We assume there are no more solutions in the negative direction and move on to $\lfloor{x}\rfloor=3$

$\lfloor{x}\rfloor=3$

We have $9-3x+2=0$ . Solving, we have $x=\frac{11}{3}$ . We see that $\lfloor{\frac{11}{3}}\rfloor=3$ , so this solution is valid

$\lfloor{x}\rfloor=4$

We have $16-3x+2=0$ . Solving, we have $x=6$ . $\lfloor{6}\rfloor\neq4$ , so this is not valid. We assume there are no more solutions.

Our final answer is $\boxed{\textbf{(B) }4}$

~kjljixx

Solution 5

Denote $a = \lfloor x \rfloor$ . Denote $b = x - \lfloor x \rfloor$ . Thus, $b \in \left[ 0 , 1 \right)$ .

The equation given in this problem can be written as $a^2 - 3 \left( a + b \right) + 2 = 0 .$

Thus, $\begin{align*} 3 b & = a^2 - 3 a + 2 . \end{align*}$

Because $b \in \left[ 0 , 1 \right)$ , we have $3 b \in \left[ 0 , 3 \right)$ . Thus, $a^2 - 3 a + 2 = 0, 1, \mbox{ or } 2 .$

If $a^2-3a+2=0$ , $(a-2)(a-1)=0$ so $a$ can be $1, 2$ .

If $a^2-3a+2=1$ , $a^2-3a+1=0$ which we find has no integer solutions after finding the discriminant.

If $a^2-3a+2=2$ , $a^2-3a=0$ -> $a(a-3)=0$ so $a$ can also be $0, 3$ .

Therefore, $a = 1$ , 2, 0, 3. Therefore, the number of solutions is $\boxed{\textbf{(B) 4}}$ .

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 6 (Quick)

A quadratic equation can have up to 2 real solutions. With the $\lfloor{x}\rfloor$ , it could also help generate another pair. We have to verify that the solutions are real and distinct.

First, we get the trivial solution by ignoring the floor. $(x-2)(x-1) = 0$ , we get $(2,1)$ as our first pair of solutions.

Up to this point, we can rule out A,E.

Next, we see that $\lfloor{x}\rfloor^2-3x=0.$ This implies that $-3x$ must be an integer. We can guess and check $x$ as $\dfrac{k}{3}$ which yields $\left(\dfrac{2}{3},\dfrac{11}{3}\right).$

So we got 4 in total $\left(\dfrac{2}{3},1,2,\dfrac{11}{3}\right).$

~Technodoggo

Solution 7

$x=1, 2$ are trivial solutions. Let $x=n+f$ for some integer $n$ and some number $f$ such that $-1<f<1$ . $\lfloor{x}\rfloor^2-3x+2= \lfloor{n+f}\rfloor^2-3(n+f)+2=n^2+-3(n+f)+2.$ So now we have $n^2-3(n+f)+2 = 0,$ which we can rewrite as $n(n-3)=3f-2.$ Since $n$ is an integer, $n(n-3)$ is an integer, so $3f-2$ is an integer. Since $-1<f<1$ , the only possible values of $f$ are $\frac{1}{3}$ , $\frac{2}{3}$ , $-\frac{1}{3}$ , and $-\frac{2}{3}$ . Plugging in each value, we find that the only value of $f$ that produces integer solutions for $n$ is $f=\frac{2}{3}$ . If $f=\frac{2}{3}$ , $n=0$ or $n=3$ . Hence, there is a total of 4 possible solutions, so the answer is $\boxed{\textbf{(B) }4}$ . ~azc1027

Solution 8

We rewrite the equation as ${\lfloor x\rfloor}^2-3\lfloor x\rfloor-3\{x\}+2=0$ , where $\{x\}$ is the fractional part of $x$

Denote $\lfloor x\rfloor = x_1$ and $\{x\} = x_2.$ Thus ${x_1}^2-3{x_1}-3{x_2}+2=0.$

By definition, $0\leq x_2\leq 1$ . We then have ${x_1}^2-3{x_1}+2=3{x_2}$ and therefore $0\leq {x_1}^2-3{x_1}+2\leq 3$ .

Solving, we have $\left[\frac{3-\sqrt{13}}{2},1\right]\cup \left[2,\frac{3+\sqrt{13}}{2}\right]$ . But since $x_1$ is an integer, we have $x_1$ can only be $0,1,2,$ or $3$ .

Testing, we see these values of $x_1$ work, and therefore the answer is just $\boxed{\textbf{(B) }4}$ .

~ESAOPS

Solution 9 (Very Fast)

We know that for integer values of x, the graph is just $x^2-3x+2$ . From the interval $[x, x+1]$ , the square stays the same, so the graph has a line segment that goes down by 3 and right by 2. This is very easy to graph, so we see that there are 4 solutions. Or, we notice that only $x = 0, 1, 2, 3$ results in a $x^2-3x+2$ in the interval $[0, 3]$ .That is $\boxed{\textbf{(B) }4}$ solutions.

~Xyco

Solution 10(has 3 cases)

define $[x] = n$

define the fractional part of $x$ as $x(f)$

thus $\lfloor{x}\rfloor^2-3x+2=0$ is

$n^2-3(n+x(f))+2=0$

$n^2-3n-3x(f)+2=0$

$n^2-3n+2$ must always be an integer and thus for this equal zero $3x(f)$ must also equal integer

thus $x(f)$ must be fraction $q/3$

and q must be 0,1,2

thus $x(f)$ must be 1/3 or 2/3 or 0/3

plugging in all

$n^2-3n-3(0)+2=0$

$n^2-3n-3(2/3)+2=0$

$n^2-3n-3(1/3)+2=0$

we simplify into

$n^2-3n+2=0$

$n^2-3n=0$

$n^2-3n+1$

where n must be a integer

just use solve for n and use only integers

we get 2 integers for the first for $x(f)=0$

$n=1,2$

$n+x(f)=x$

$1+0=1$

$2+0=2$

$x=1,2$

we get 2 integers for the second for $x(f)=2/3$

$n=0,3$

$n+x(f)=x$

$0+2/3=2/3$

$3+2/3=11/3$

We get ZERO integers for the third for $x(f)=1/3$

we get use the quadratic discriminant to see $\sqrt{b^{2}-4ac}$

Our equation is $n^2-3n+1$

$\sqrt{3^{2}-4(1)(1)}$ yielding a non integer value which means this case is invalid

we count a total of 4 solutions which are $x=2/3,1,2,11/3$

Our answer is

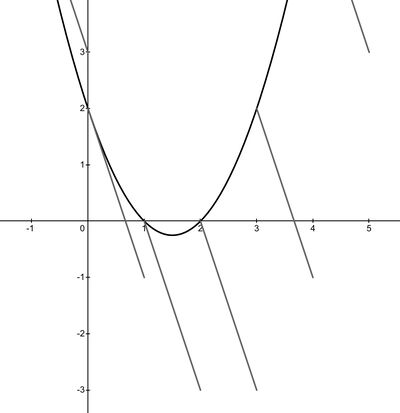
Solution 11 (Based on graph)

For $\lfloor x \rfloor^2 - 3x + 2 = 0$ , there is a discontinuity at each integer value of $x$ , and it also lies on the non-floor version of the function. Between each integer $x$ and the next forms a line with a slope of $-3$ . This simplifies the task of sketching the function's graph. Note that the points at $1$ and $2$ are considered intersections because they are points on the left side of each integer interval that exactly lie on $y = 0$ . Thus, we conclude there are $4$ intersection points, and the answer is $\boxed{(\text{B}) \ 4}$ . ～Athmyx

Video Solution 1 by OmegaLearn

https://youtu.be/wAYcpn-Q_KQ

Video Solution 2 by SpreadTheMathLove

https://www.youtube.com/watch?v=DvHGEXBjf0Y

Video Solution

https://youtu.be/ONRoop23LIY