2023 IMO Problems/Problem 6
Problem
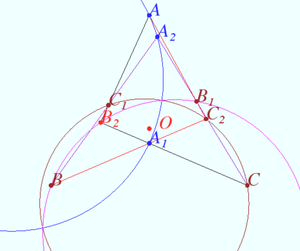
Let ![]() be an equilateral triangle. Let
be an equilateral triangle. Let ![]() be interior points of
be interior points of ![]() such that
such that ![]() ,
, ![]() ,
, ![]() , and
, and
![]() Let
Let ![]() and
and ![]() meet at
meet at ![]() let
let ![]() and
and ![]() meet at
meet at ![]() and let
and let ![]() and
and ![]() meet at
meet at ![]()
Prove that if triangle ![]() is scalene, then the three circumcircles of triangles
is scalene, then the three circumcircles of triangles ![]() and
and ![]() all pass through two common points.
all pass through two common points.
(Note: a scalene triangle is one where no two sides have equal length.)
Solution
https://www.youtube.com/watch?v=jZNIpapyGJQ [Video contains solutions to all day 2 problems, it was created by a man known as Najeeb Abdullah, who qualified in the IMO from the time he was 6 years old]
See Also
| 2023 IMO (Problems) • Resources | ||
| Preceded by Problem 5 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Last Problem |
| All IMO Problems and Solutions | ||