2024 AIME I Problems/Problem 10
Contents
[hide]Problem
Let ![]() have side lengths
have side lengths ![]() ,
, ![]() ,
, ![]() . The tangents to circumcircle of
. The tangents to circumcircle of ![]() at
at ![]() and
and ![]() intersect at point
intersect at point ![]() , and
, and ![]() intersects the circumcircle at
intersects the circumcircle at ![]() . The length of
. The length of ![]() is equal to
is equal to ![]() , where
, where ![]() and
and ![]() are relatively prime integers. Find
are relatively prime integers. Find ![]() .
.
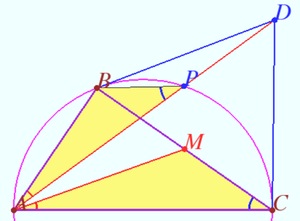
Diagram
![[asy] import olympiad; unitsize(15); pair A, B, C, D, E, F, P, O; C = origin; A = (10,0); B = (7.8, 4.4899); draw(A--B--C--cycle); draw(A..B..C..cycle, red+dotted); O = circumcenter(A, B, C); E = rotate(90,B) * (O); F = rotate(90,C) * (O); D = IP(B..E + (B-E)*4, C..F + (C-F)*-3); draw(B--D--C--D--A); P = IP(D..A, A..B..C); dot(A); dot(B); dot(C); dot(D); dot(P); label("$A$", A, dir(335)); label("$B$", B, dir(65)); label("$C$", C, dir(200)); label("$D$", D, dir(135)); label("$P$", P, dir(235)); [/asy]](http://latex.artofproblemsolving.com/1/5/9/15925619d38c6533169fedb4323623e7d6ecb692.png)
Solution 1
We have ![]() from the tangency condition. With LoC we have
from the tangency condition. With LoC we have ![]() and
and ![]() . Then,
. Then, ![]() . Using LoC we can find
. Using LoC we can find ![]() :
: ![]() . Thus,
. Thus, ![]() . By Power of a Point,
. By Power of a Point, ![]() so
so ![]() which gives
which gives ![]() . Finally, we have
. Finally, we have ![]() . So the answer is
. So the answer is ![]() .
.
~angie.
Solution 2
We know ![]() is the symmedian (see Symmedian and tangents ) ,
is the symmedian (see Symmedian and tangents ) ,
which implies that ![]() where
where ![]() is the midpoint of
is the midpoint of ![]() .
.
By Appolonius' theorem, ![]() .
.
Thus, we have ![]()
~Bluesoul
Solution 3
Extend sides ![]() and
and ![]() to points
to points ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() and
and ![]() are the feet of the altitudes in
are the feet of the altitudes in ![]() . Denote the feet of the altitude from
. Denote the feet of the altitude from ![]() to
to ![]() as
as ![]() , and let
, and let ![]() denote the orthocenter of
denote the orthocenter of ![]() . Call
. Call ![]() the midpoint of segment
the midpoint of segment ![]() . By the Three Tangents Lemma, we have that
. By the Three Tangents Lemma, we have that ![]() and
and ![]() are both tangents to
are both tangents to ![]()
![]()
![]() , and since
, and since ![]() is the midpoint of
is the midpoint of ![]() ,
, ![]() . Additionally, by angle chasing, we get that:
. Additionally, by angle chasing, we get that:
![]() Also,
Also,
![]() Furthermore,
Furthermore,
![]() From this, we see that
From this, we see that ![]() with a scale factor of
with a scale factor of ![]() . By the Law of Cosines,
. By the Law of Cosines,
![]() Thus, we can find that the side lengths of
Thus, we can find that the side lengths of ![]() are
are ![]() . Then, by Stewart's theorem,
. Then, by Stewart's theorem, ![]() . By Power of a Point,
. By Power of a Point,
![]()
![]() Thus,
Thus,
![]() Therefore, the answer is
Therefore, the answer is ![]() .
.
~mathwiz_1207
Solution 4 (LoC spam)
Connect lines ![]() and
and ![]() . From the angle by tanget formula, we have
. From the angle by tanget formula, we have ![]() . Therefore by AA similarity,
. Therefore by AA similarity, ![]() . Let
. Let ![]() . Using ratios, we have
. Using ratios, we have ![]() Similarly, using angle by tangent, we have
Similarly, using angle by tangent, we have ![]() , and by AA similarity,
, and by AA similarity, ![]() . By ratios, we have
. By ratios, we have ![]() However, because
However, because ![]() , we have
, we have ![]() so
so ![]() Now using Law of Cosines on
Now using Law of Cosines on ![]() in triangle
in triangle ![]() , we have
, we have ![]() Solving, we find
Solving, we find ![]() . Now we can solve for
. Now we can solve for ![]() . Using Law of Cosines on
. Using Law of Cosines on ![]() we have
we have
Solving, we get ![]() Now we have a system of equations using Law of Cosines on
Now we have a system of equations using Law of Cosines on ![]() and
and ![]() ,
, ![]()
![]()
Solving, we find ![]() , so our desired answer is
, so our desired answer is ![]() .
.
~evanhliu2009
Solution 5
Following from the law of cosines, we can easily get ![]() ,
, ![]() ,
, ![]() .
.
Hence, ![]() ,
, ![]() ,
, ![]() .
Thus,
.
Thus, ![]() .
.
Denote by ![]() the circumradius of
the circumradius of ![]() .
In
.
In ![]() , following from the law of sines, we have
, following from the law of sines, we have ![]() .
.
Because ![]() and
and ![]() are tangents to the circumcircle
are tangents to the circumcircle ![]() ,
, ![]() and
and ![]() .
Thus,
.
Thus, ![]() .
.
In ![]() , we have
, we have ![]() and
and ![]() .
Thus, following from the law of cosines, we have
.
Thus, following from the law of cosines, we have
Following from the law of cosines,
Therefore,
Therefore, the answer is ![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Video Solution 1 by OmegaLearn.org
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 6
Note that since P is a symmedian, ![]() are harmonic. As a result,
are harmonic. As a result, ![]() . As a result,
. As a result, ![]() . Call
. Call ![]() . Then,
. Then, ![]() . Since
. Since ![]() ,
, ![]() . Use LOC to find
. Use LOC to find ![]() . Finish with Ptolemy on ABPC, and finish to get
. Finish with Ptolemy on ABPC, and finish to get ![]() .
.
Solution 7 (1 min solve)
Note that ![]() is the A-symmedian in
is the A-symmedian in ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() . It is a well known property that
. It is a well known property that ![]() . Therefore, using the median length formula,
. Therefore, using the median length formula, ![]() so
so ![]() so our answer is
so our answer is ![]() .
.
See also
| 2024 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()