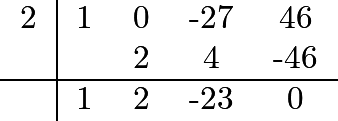2024 AIME I Problems/Problem 15
Contents
[hide]- 1 Problem
- 2 Solution 1
- 3 Solution 2 (constrained optimization with Lagrangian multiplier)
- 4 Solution 3 (Vieta's Formula and Rational Root Theroem)
- 5 Solution 3a (Derivative)
- 6 Solution 4
- 7 Solution 5
- 8 Solution 6 (If you don't notice that two of the side lengths have to be equal)
- 9 Video Solution 1 by OmegaLearn.org (super short)
- 10 Video Solution 2 (constrained optimization with Lagrangian multiplier)
- 11 Video Solution 3 by Kaguya Shinomiya (thorough analysis)
- 12 See also
Problem
Let ![]() be the set of rectangular boxes with surface area
be the set of rectangular boxes with surface area ![]() and volume
and volume ![]() . Let
. Let ![]() be the radius of the smallest sphere that can contain each of the rectangular boxes that are elements of
be the radius of the smallest sphere that can contain each of the rectangular boxes that are elements of ![]() . The value of
. The value of ![]() can be written as
can be written as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
Observe that the "worst" possible box is one of the maximum possible length.
By symmetry, the height and the width are the same in this antioptimal box. (If the height and width weren't the same, the extra difference between them could be used to make the length longer.) Thus, let the width and height be of length ![]() and the length be
and the length be ![]() .
.
We're given that the volume is ![]() ; thus,
; thus, ![]() . We're also given that the surface area is
. We're also given that the surface area is ![]() ; thus,
; thus, ![]() .
.
From the first equation, we can get ![]() . We do a bunch of algebra:
. We do a bunch of algebra:
We can use the Rational Root Theorem and test a few values. It turns out that ![]() works. We use synthetic division to divide by
works. We use synthetic division to divide by ![]() :
:
As we expect, the remainder is ![]() , and we are left with the polynomial
, and we are left with the polynomial ![]() . We can now simply use the quadratic formula and find that the remaining roots are
. We can now simply use the quadratic formula and find that the remaining roots are ![]() . We want the smallest
. We want the smallest ![]() to maximize
to maximize ![]() , and it turns out that
, and it turns out that ![]() is in fact the smallest root. Thus, we let
is in fact the smallest root. Thus, we let ![]() . Substituting this into
. Substituting this into ![]() , we find that
, we find that ![]() . However, this is not our answer! This is simply the length of the box; we want the radius of the sphere enclosing it. We know that the diameter of the sphere is the diagonal of the box, and the 3D Pythagorean Theorem can give us the space diagonal. Applying it, we find that the diagonal has length
. However, this is not our answer! This is simply the length of the box; we want the radius of the sphere enclosing it. We know that the diameter of the sphere is the diagonal of the box, and the 3D Pythagorean Theorem can give us the space diagonal. Applying it, we find that the diagonal has length  . This is the diameter; we halve it to find the radius,
. This is the diameter; we halve it to find the radius, ![]() . We then square this and end up with
. We then square this and end up with ![]() , giving us an answer of
, giving us an answer of ![]() .
.
~Technodoggo
Solution 2 (constrained optimization with Lagrangian multiplier)
Denote by ![]() ,
, ![]() ,
, ![]() the length, width, and height of a rectangular box.
We have
the length, width, and height of a rectangular box.
We have
We have
Therefore, we solve the following constrained optimization problem:
First, we prove that an optimal solution must have at least two out of ![]() ,
, ![]() ,
, ![]() that are the same.
that are the same.
Denote by ![]() and
and ![]() lagrangian multipliers of constraints (1) and (2), respectively.
Consider the following Lagrangian:
lagrangian multipliers of constraints (1) and (2), respectively.
Consider the following Lagrangian:
Taking first-order-condition with respect to ![]() ,
, ![]() ,
, ![]() , respectively, we get
, respectively, we get
Suppose there is an optimal solution with ![]() ,
, ![]() ,
, ![]() that are all distinct.
that are all distinct.
Taking ![]() , we get
, we get
![]()
Because ![]() , we have
, we have
![]()
Analogously, we have
Taking ![]() , we get
, we get ![]() .
Because
.
Because ![]() , we have
, we have ![]() . Plugging this into (6), we get
. Plugging this into (6), we get ![]() .
.
However, the solution that ![]() is a contradiction with (3).
Therefore, in an optimal solution, we cannot have
is a contradiction with (3).
Therefore, in an optimal solution, we cannot have ![]() ,
, ![]() , and
, and ![]() to be all distinct.
to be all distinct.
W.L.O.G, in our remaining analysis, we assume an optimal solution satisfies ![]() .
.
Therefore, we need to solve the following two-variable optimization problem:
Replacing ![]() with
with ![]() by using the constraint
by using the constraint ![]() , we solve the following single-variable optimization problem:
, we solve the following single-variable optimization problem:
By solving (9), we get ![]() and
and ![]() .
.
Plugging ![]() into (8), we get
into (8), we get ![]() .
.
Plugging ![]() into (8), we get
into (8), we get ![]() .
.
We have ![]() .
Therefore, the maximum value of
.
Therefore, the maximum value of ![]() is
is ![]() .
.
Therefore,
Therefore, the answer is
![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 3 (Vieta's Formula and Rational Root Theroem)
First, let's list the conditions:
Denote by ![]() ,
, ![]() ,
, ![]() the length, width, and height of a rectangular box.
the length, width, and height of a rectangular box.
![]()
We can spot Vieta's formula hidden inside this equation and call this ![]() . Now we have three equations:
. Now we have three equations:
![]()
![]()
![]()
Let there be a cubic equation. ![]() . Its roots are
. Its roots are ![]() ,
, ![]() and
and ![]() . We can use our formulas from before to derive
. We can use our formulas from before to derive ![]() and
and ![]() .
.
![]()
![]()
![]()
We can now rewrite the equation from before:
![]()
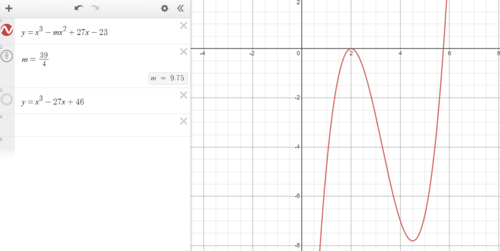
To find the maximum ![]() we need the maximum
we need the maximum ![]() . This only occurs when this equation has double roots illustrated with graph below.
. This only occurs when this equation has double roots illustrated with graph below.
WLOG we can set ![]() .
.
Thus:
![]()
![]()
We can substitute ![]() and form a depressed cubic equation with
and form a depressed cubic equation with ![]() .
.
![]()
A quick test reveals that ![]() is a root of the equation. Comparing coefficients we can factorize the equation into:
is a root of the equation. Comparing coefficients we can factorize the equation into:
![]()
Besides ![]() , we derive another positive root using the quadratic formula,
, we derive another positive root using the quadratic formula, ![]() But to maximize the
But to maximize the ![]() we need to pick the smaller
we need to pick the smaller ![]() , which is
, which is ![]() .
.
Substituting this into ![]() , we find that
, we find that ![]() .
.
Applying it to our equation above:
![]() .
.
Solution 3a (Derivative)
to find the maximum m for ![]()
rewrite ![]() as function of
as function of ![]() and calculate derivatives to get maximum value,
and calculate derivatives to get maximum value, ![]()
![]()
![]()
![]()
when ![]() ,
, ![]() the rest is similar to solution 3
the rest is similar to solution 3
Solution 4
This question looks complex, but once converted into a number theory problem, it becomes elementary. We know, if the dimensions are taken to be numbers in the form of coprime numbers p/q,q/r, and r, it is immediately obvious that p=23.
And solving we get: ![]() We know length cannot be -ve, in this case, therefore, q=4. And, again, we see:
We know length cannot be -ve, in this case, therefore, q=4. And, again, we see:
![]() giving rise to r=2.
For a cuboid inside a circle, we know:the radius is half its diagonal or, can we not say,
giving rise to r=2.
For a cuboid inside a circle, we know:the radius is half its diagonal or, can we not say,
![]() or here,
or here,
![]() so here,
so here, ![]()
~Grammaticus
Solution 5
This problem essentially boils down to maximizing the value of ![]() (where
(where ![]() ,
, ![]() , and
, and ![]() denote the dimensions of the box) given
denote the dimensions of the box) given ![]() and
and ![]() . After doing so, we can calculate
. After doing so, we can calculate ![]() using
using ![]() (as in Solution 2). We can turn
(as in Solution 2). We can turn ![]() into an expression in terms of only
into an expression in terms of only ![]() and use the method of critical points. Since
and use the method of critical points. Since ![]() , we have
, we have ![]() and thus
and thus ![]() . Isolating
. Isolating ![]() , we find
, we find ![]() , so
, so![]() We have turned
We have turned ![]() into an equation in
into an equation in ![]() , using all conditions the problem has given us. We proceed with calculus. The maximum value of this function in
, using all conditions the problem has given us. We proceed with calculus. The maximum value of this function in ![]() is one of the critical points of this function, which can be calculated by equating the function's derivative with
is one of the critical points of this function, which can be calculated by equating the function's derivative with ![]() . Using the power rule, the derivative of
. Using the power rule, the derivative of ![]() is
is ![]() . Equating
. Equating ![]() to zero, we get
to zero, we get![]() The roots of this can be found using the rational root theorem, yielding
The roots of this can be found using the rational root theorem, yielding ![]() or
or ![]() . Don't forget --
. Don't forget -- ![]() must be positive, so the only possible candidates of
must be positive, so the only possible candidates of ![]() to maximize
to maximize ![]() are
are ![]() and
and ![]() . Plugging both of them into
. Plugging both of them into ![]() , we find
, we find ![]() yields a greater result,
yields a greater result, ![]() . Thus, the maximum value of
. Thus, the maximum value of ![]() is
is ![]() . Therefore, the value of
. Therefore, the value of ![]() is
is![]()
Solution 6 (If you don't notice that two of the side lengths have to be equal)
From the previous solutions we can see that we have to maximize ![]() in the expression
in the expression ![]() such that
such that ![]() has
has ![]() real and positive roots since the roots correspond to the side lengths of the rectangle. To do this we can use synthetic division to divide this expression by
real and positive roots since the roots correspond to the side lengths of the rectangle. To do this we can use synthetic division to divide this expression by ![]() for some arbitrary root
for some arbitrary root ![]() to try and see how
to try and see how ![]() relates to the roots. After doing synthetic division, we get
relates to the roots. After doing synthetic division, we get ![]() Since we defined r to be a root of the expression, it must divide into it with no remainder, meaning that
Since we defined r to be a root of the expression, it must divide into it with no remainder, meaning that
![]() or
or ![]()
We can now substitute this value into ![]() to get
to get
![]() .
.
Multiplying everything by ![]() yields
yields ![]() .
.
We now have to find the maximum value of ![]() for which this expression has 2 roots, since
for which this expression has 2 roots, since ![]() strictly increases
with
strictly increases
with ![]() from our previous expression of
from our previous expression of ![]()
To do this, we can find the discriminant of ![]() and find the maximum value of
and find the maximum value of ![]() for which it is positive.
for which it is positive.
The discriminant of this expression is ![]() , and after using the rational root theorem we can find
, and after using the rational root theorem we can find ![]() as a root.
as a root.
The remaining expression is ![]() .
We can quickly see using the quadratic formula that
.
We can quickly see using the quadratic formula that ![]() is the largest root, meaning that
is the largest root, meaning that ![]() is the largest value that a root of
is the largest value that a root of ![]() can have for which
can have for which ![]() has
has ![]() positive, real solutions. From here, we can substitute this value back into the expression for
positive, real solutions. From here, we can substitute this value back into the expression for ![]() , giving us
, giving us ![]() . The length of the radius squared is
. The length of the radius squared is ![]() and
and ![]()
~Lapcas
Video Solution 1 by OmegaLearn.org (super short)
Video Solution 2 (constrained optimization with Lagrangian multiplier)
https://www.youtube.com/watch?v=KjEy2Ju2z8A
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Video Solution 3 by Kaguya Shinomiya (thorough analysis)
https://www.youtube.com/watch?v=mkSbqG8jly0&t=38s
See also
| 2024 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()