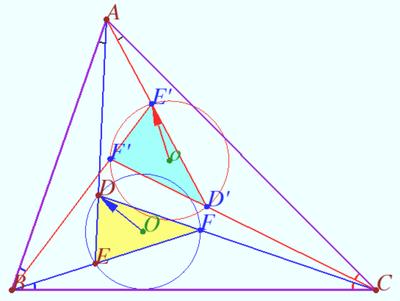
Isogonal conjugate
Isogonal conjugates are pairs of points in the plane with respect to a certain triangle.
Contents
[hide]- 1 The isogonal theorem
- 2 Parallel segments
- 3 Perpendicularity
- 4 Fixed point
- 5 Bisector
- 6 Isogonal of the diagonal of a quadrilateral
- 7 Isogonals in trapezium
- 8 Isogonals in complete quadrilateral
- 9 Isogonal of the bisector of the triangle
- 10 Points on isogonals
- 11 Trapezoid
- 12 Definition of isogonal conjugate of a point
- 13 Three points
- 14 Second definition
- 15 Distance to the sides of the triangle
- 16 Sign of isogonally conjugate points
- 17 Circumcircle of pedal triangles
- 18 Common circumcircle of the pedal triangles as the sign of isogonally conjugate points
- 19 Two pares of isogonally conjugate points
- 20 Circles
- 21 Equidistant isogonal conjugate points
- 22 Simplified distance formula for isogonal points
- 23 Point on circumcircle
- 24 Fixed point on circumcircle
- 25 Distance formula for isogonal points
- 26 Miquel point for isogonal conjugate points
- 27 Point on circumcircle
- 28 Isogonal of line BC with respect to angle BAC
- 29 Isogonal bijection lines and points
- 30 Miquel point for two pare isogonal points
- 31 Isogonic center’s conjugate point
- 32 Three pairs isogonal points
- 33 Ratio for three pairs of isogonal points
- 34 Problems
The isogonal theorem
Isogonal lines definition
Let a line ![]() and a point
and a point ![]() lying on
lying on ![]() be given. A pair of lines symmetric with respect to
be given. A pair of lines symmetric with respect to ![]() and containing the point
and containing the point ![]() be called isogonals with respect to the pair
be called isogonals with respect to the pair ![]()
Sometimes it is convenient to take one pair of isogonals as the base one, for example, ![]() and
and ![]() are the base pair. Then we call the remaining pairs as isogonals with respect to the angle
are the base pair. Then we call the remaining pairs as isogonals with respect to the angle ![]()
Projective transformation
It is known that the transformation that maps a point with coordinates ![]() into a point with coordinates
into a point with coordinates ![]() is projective.
is projective.
If the abscissa axis coincides with the line ![]() and the origin coincides with the point
and the origin coincides with the point ![]() then the isogonals define the equations
then the isogonals define the equations ![]() and the lines
and the lines ![]() symmetrical with respect to the line
symmetrical with respect to the line ![]() become their images.
become their images.
It is clear that, under the converse transformation (also projective), such pairs of lines become isogonals, and the points equidistant from ![]() lie on the isogonals.
lie on the isogonals.
The isogonal theorem
Let two pairs of isogonals ![]() and
and ![]() with respect to the pair
with respect to the pair ![]() be given. Denote
be given. Denote ![]()
Prove that ![]() and
and ![]() are the isogonals with respect to the pair
are the isogonals with respect to the pair ![]()
Proof
Let us perform a projective transformation of the plane that maps the point ![]() into a point at infinity and the line
into a point at infinity and the line ![]() maps to itself. In this case, the isogonals turn into a pair of straight lines parallel to
maps to itself. In this case, the isogonals turn into a pair of straight lines parallel to ![]() and equidistant from
and equidistant from ![]()
The converse (also projective) transformation maps the points equidistant from ![]() onto isogonals. We denote the image and the preimage with the same symbols.
onto isogonals. We denote the image and the preimage with the same symbols.
Let the images of isogonals are vertical lines. Let coordinates of images of points be ![]() Equation of a straight line
Equation of a straight line ![]() is
is ![]()
Equation of a straight line ![]() is
is ![]()
The abscissa ![]() of the point
of the point ![]() is
is ![]()
Equation of a straight line ![]() is
is ![]()
Equation of a straight line ![]() is
is ![]()
The abscissa ![]() of the point
of the point ![]() is
is ![]()
Preimages of the points ![]() and
and ![]() lie on the isogonals.
lie on the isogonals. ![]()
The isogonal theorem in the case of parallel lines
Let ![]() and
and ![]() are isogonals with respect
are isogonals with respect ![]()
Let lines ![]() and
and ![]() intersect at point
intersect at point ![]()
Prove that ![]() and line
and line ![]() through
through ![]() parallel to
parallel to ![]() are the isogonals with respect
are the isogonals with respect ![]()
Proof
The preimage of ![]() is located at infinity on the line
is located at infinity on the line ![]()
The equality ![]() implies the equality the slopes modulo of
implies the equality the slopes modulo of ![]() and
and ![]() to the bisector of
to the bisector of ![]()
Converse theorem
Let lines ![]() and
and ![]() intersect at point
intersect at point ![]()
Let ![]() and
and ![]() be the isogonals with respect
be the isogonals with respect ![]()
Prove that ![]() and
and ![]() are isogonals with respect
are isogonals with respect ![]()
Proof
The preimage of ![]() is located at infinity on the line
is located at infinity on the line ![]() so the slope of
so the slope of ![]() is known.
is known.
Suppose that ![]()
The segment ![]() and the lines
and the lines ![]() are fixed
are fixed ![]()
![]() intersects
intersects ![]() at
at ![]()
but there is the only point where line ![]() intersect
intersect ![]() Сontradiction.
Сontradiction. ![]()
vladimir.shelomovskii@gmail.com, vvsss
Parallel segments
Let triangle ![]() be given. Let
be given. Let ![]() and
and ![]() be the isogonals with respect
be the isogonals with respect ![]() Let
Let ![]()
Prove that ![]() lies on bisector of
lies on bisector of ![]() and
and ![]()
Proof
Both assertions follow from The isogonal theorem in the case of parallel lines
vladimir.shelomovskii@gmail.com, vvsss
Perpendicularity
Let triangle ![]() be given. Right triangles
be given. Right triangles ![]() and
and ![]() with hypotenuses
with hypotenuses ![]() and
and ![]() are constructed on sides
are constructed on sides ![]() and
and ![]() to the outer (inner) side of
to the outer (inner) side of ![]() Let
Let ![]() Prove that
Prove that ![]()
Proof
Let ![]() be the bisector of
be the bisector of ![]()
![]() and
and ![]() are isogonals with respect to the pair
are isogonals with respect to the pair ![]()
![]() and
and ![]() are isogonals with respect to the pair
are isogonals with respect to the pair ![]()
![]() and
and ![]() are isogonals with respect to the pair
are isogonals with respect to the pair ![]() in accordance with The isogonal theorem.
in accordance with The isogonal theorem.
![]()
![]() is the diameter of circumcircle of
is the diameter of circumcircle of ![]()
Circumradius and altitude are isogonals with respect bisector and vertex of triangle, so ![]()
![]()
vvsss
Fixed point
Let fixed triangle ![]() be given. Let points
be given. Let points ![]() and
and ![]() on sidelines
on sidelines ![]() and
and ![]() respectively be the arbitrary points.
respectively be the arbitrary points.
Let ![]() be the point on sideline
be the point on sideline ![]() such that
such that ![]()
![]() Prove that line
Prove that line ![]() pass through the fixed point.
pass through the fixed point.
Proof
We will prove that point ![]() symmetric
symmetric ![]() with respect
with respect ![]() lies on
lies on ![]() .
.
![]() and
and ![]() are isogonals with respect to
are isogonals with respect to ![]()
![]() points
points ![]() and
and ![]() lie on isogonals with respect to
lie on isogonals with respect to ![]() in accordance with The isogonal theorem.
in accordance with The isogonal theorem.
Point ![]() symmetric
symmetric ![]() with respect
with respect ![]() lies on isogonal
lies on isogonal ![]() with respect to
with respect to ![]() that is
that is ![]()
![]()
vvsss
Bisector
Let a convex quadrilateral ![]() be given. Let
be given. Let ![]() and
and ![]() be the incenters of triangles
be the incenters of triangles ![]() and
and ![]() respectively.
respectively.
Let ![]() and
and ![]() be the A-excenters of triangles
be the A-excenters of triangles ![]() and
and ![]() respectively.
respectively. ![]()
Prove that ![]() is the bisector of
is the bisector of ![]()
Proof
![]()
![]() and
and ![]() are isogonals with respect to the angle
are isogonals with respect to the angle ![]()
![]() and
and ![]() are isogonals with respect to the angle
are isogonals with respect to the angle ![]() in accordance with The isogonal theorem.
in accordance with The isogonal theorem.
Denote ![]()
WLOG, ![]()
![]()
![]()
vvsss
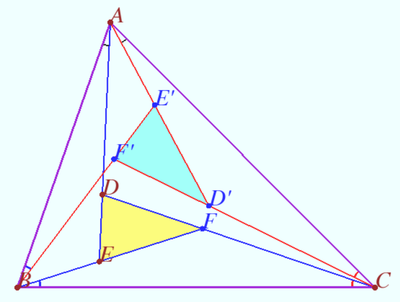
Isogonal of the diagonal of a quadrilateral
Given a quadrilateral ![]() and a point
and a point ![]() on its diagonal such that
on its diagonal such that ![]()
Let ![]()
Prove that ![]()
Proof
Let us perform a projective transformation of the plane that maps the point ![]() to a point at infinity and the line
to a point at infinity and the line ![]() into itself.
into itself.
In this case, the images of points ![]() and
and ![]() are equidistant from the image of
are equidistant from the image of ![]()
the point ![]() (midpoint of
(midpoint of ![]() lies on
lies on ![]()
![]() contains the midpoints of
contains the midpoints of ![]() and
and ![]()
![]() is the Gauss line of the complete quadrilateral
is the Gauss line of the complete quadrilateral ![]()
![]() bisects
bisects ![]()
the preimages of the points ![]() and
and ![]() lie on the isogonals
lie on the isogonals ![]() and
and ![]()
vvsss
Isogonals in trapezium
Let the trapezoid ![]() be given. Denote
be given. Denote ![]()
The point ![]() on the smaller base
on the smaller base ![]() is such that
is such that ![]()
Prove that ![]()
Proof
![]()
![]() Therefore
Therefore ![]() and
and ![]() are isogonals with respect
are isogonals with respect ![]()
Let us perform a projective transformation of the plane that maps the point ![]() to a point at infinity and the line
to a point at infinity and the line ![]() into itself.
into itself.
In this case, the images of points ![]() and
and ![]() are equidistant from the image of
are equidistant from the image of ![]() contains the midpoints of
contains the midpoints of ![]() and
and ![]() , that is,
, that is, ![]() is the Gauss line of the complete quadrilateral
is the Gauss line of the complete quadrilateral ![]()
![]() bisects
bisects ![]()
The preimages of the points ![]() and
and ![]() lie on the isogonals
lie on the isogonals ![]() and
and ![]()
vvsss
Isogonals in complete quadrilateral
Let complete quadrilateral ![]() be given. Let
be given. Let ![]() be the Miquel point of
be the Miquel point of ![]()
Prove that ![]() is isogonal to
is isogonal to ![]() and
and ![]() is isogonal to
is isogonal to ![]() with respect
with respect ![]()
Proof
![]()
![]()
vvsss
Isogonal of the bisector of the triangle
The triangle ![]() be given. The point
be given. The point ![]() chosen on the bisector
chosen on the bisector ![]()
Denote ![]()
![]() Prove that
Prove that ![]()
Proof
Let us perform a projective transformation of the plane that maps the point ![]() to a point at infinity and the line
to a point at infinity and the line ![]() into itself.
into itself.
In this case, the images of segments ![]() and
and ![]() are equidistant from the image of
are equidistant from the image of ![]()
Image of point ![]() is midpoint of image
is midpoint of image ![]() and midpoint image
and midpoint image ![]()
Image ![]() is parallelogramm
is parallelogramm ![]()
![]() distances from
distances from ![]() and
and ![]() to
to ![]() are equal
are equal ![]()
Preimages ![]() and
and ![]() are isogonals with respect
are isogonals with respect ![]()
vladimir.shelomovskii@gmail.com, vvsss
Points on isogonals
The triangle ![]() be given. The point
be given. The point ![]() chosen on
chosen on ![]() The point
The point ![]() chosen on
chosen on ![]() such that
such that ![]() and
and ![]() are isogonals with respect
are isogonals with respect ![]()
Prove that ![]()
Proof
Denote ![]()
![]()
![]()
We use the Law of Sines and get:
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
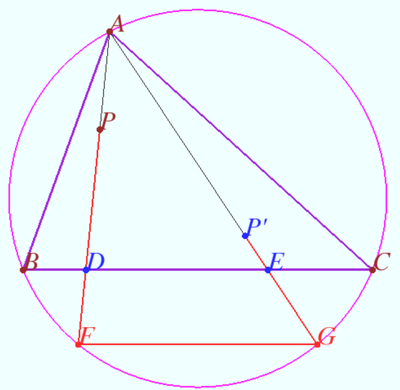
Trapezoid
The lateral side ![]() of the trapezoid
of the trapezoid ![]() is perpendicular to the bases, point
is perpendicular to the bases, point ![]() is the intersection point of the diagonals
is the intersection point of the diagonals ![]() .
.
Point ![]() is taken on the circumcircle
is taken on the circumcircle ![]() of triangle
of triangle ![]() diametrically opposite to point
diametrically opposite to point ![]()
Prove that ![]()
Proof
WLOG, ![]() is not the diameter of
is not the diameter of ![]() Let sidelines
Let sidelines ![]() and
and ![]() intersect
intersect ![]() at points
at points ![]() and
and ![]() respectively.
respectively.
![]() is rectangle
is rectangle ![]()
![]()
![]() is isogonal to
is isogonal to ![]() with respect
with respect ![]()
![]() is isogonal to
is isogonal to ![]() with respect
with respect ![]()
In accordance with The isogonal theorem in case parallel lines ![]()
![]() is isogonal to
is isogonal to ![]() with respect
with respect ![]()
![]() in accordance with Converse theorem for The isogonal theorem in case parallel lines.
in accordance with Converse theorem for The isogonal theorem in case parallel lines. ![]()
vladimir.shelomovskii@gmail.com, vvsss
Definition of isogonal conjugate of a point
Let triangle ![]() be given. Let
be given. Let ![]() be the circumcircle of
be the circumcircle of ![]() Let point
Let point ![]() be in the plane of
be in the plane of ![]() Denote by
Denote by ![]() the lines
the lines ![]() respectively. Denote by
respectively. Denote by ![]() the lines
the lines ![]() ,
, ![]() ,
, ![]() , respectively.
Denote by
, respectively.
Denote by ![]() ,
, ![]() ,
, ![]() the reflections of
the reflections of ![]() ,
, ![]() ,
, ![]() over the angle bisectors of angles
over the angle bisectors of angles ![]() ,
, ![]() ,
, ![]() , respectively.
, respectively.
Prove that lines ![]() ,
, ![]() ,
, ![]() concur at a point
concur at a point ![]() This point is called the isogonal conjugate of
This point is called the isogonal conjugate of ![]() with respect to triangle
with respect to triangle ![]() .
.
Proof
By our constructions of the lines ![]() ,
, ![]() , and this statement remains true after permuting
, and this statement remains true after permuting ![]() . Therefore by the trigonometric form of Ceva's Theorem
. Therefore by the trigonometric form of Ceva's Theorem
![]() so again by the trigonometric form of Ceva, the lines
so again by the trigonometric form of Ceva, the lines ![]() concur, as was to be proven.
concur, as was to be proven. ![]()
Corollary
Let points P and Q lie on the isogonals with respect angles ![]() and
and ![]() of triangle
of triangle ![]()
Then these points lie on isogonals with respect angle ![]()
Corollary 2
Let point ![]() be in the sideline
be in the sideline ![]() of
of ![]()
Then the isogonal conjugate of a point ![]() is a point
is a point ![]()
Points ![]() and
and ![]() do not have an isogonally conjugate point.
do not have an isogonally conjugate point.
vladimir.shelomovskii@gmail.com, vvsss
Three points
Let fixed triangle ![]() be given. Let the arbitrary point
be given. Let the arbitrary point ![]() not be on sidelines of
not be on sidelines of ![]() Let
Let ![]() be the point on isogonal of
be the point on isogonal of ![]() with respect angle
with respect angle ![]() Let
Let ![]() be the crosspoint of isogonal of
be the crosspoint of isogonal of ![]() with respect angle
with respect angle ![]() and isogonal of
and isogonal of ![]() with respect angle
with respect angle ![]()
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Denote ![]()
![]() and
and ![]() are isogonals with respect
are isogonals with respect ![]()
![]() and S lie on isogonals of
and S lie on isogonals of ![]()
![]()
![]() is isogonal conjugated of
is isogonal conjugated of ![]() with respect
with respect ![]()
![]() and
and ![]() lie on isogonals of
lie on isogonals of ![]()
Therefore points ![]() and
and ![]() lie on the same line which is isogonal to
lie on the same line which is isogonal to ![]() with respect
with respect ![]()
vladimir.shelomovskii@gmail.com, vvsss
Second definition
Let triangle ![]() be given. Let point
be given. Let point ![]() lies in the plane of
lies in the plane of ![]()
![]() Let the reflections of
Let the reflections of ![]() in the sidelines
in the sidelines ![]() be
be ![]()
Then the circumcenter ![]() of the
of the ![]() is the isogonal conjugate of
is the isogonal conjugate of ![]()
Points ![]() and
and ![]() have not isogonal conjugate points.
have not isogonal conjugate points.
Another points of sidelines ![]() have points
have points ![]() respectively as isogonal conjugate points.
respectively as isogonal conjugate points.
Proof
![]()
![]()
![]()
![]() is common therefore
is common therefore
![]() Similarly
Similarly ![]() is the circumcenter of the
is the circumcenter of the ![]()
![]()
From definition 1 we get that ![]() is the isogonal conjugate of
is the isogonal conjugate of ![]()
It is clear that each point ![]() has the unique isogonal conjugate point.
has the unique isogonal conjugate point.
Let point ![]() be the point with barycentric coordinates
be the point with barycentric coordinates ![]()
![]() Then
Then ![]() has barycentric coordinates
has barycentric coordinates ![]()
vladimir.shelomovskii@gmail.com, vvsss
Distance to the sides of the triangle
Let ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Let ![]() and
and ![]() be the projection
be the projection ![]() on sides
on sides ![]() and
and ![]() respectively.
respectively.
Let ![]() and
and ![]() be the projection
be the projection ![]() on sides
on sides ![]() and
and ![]() respectively.
respectively.
Then ![]()
Proof
Let ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Sign of isogonally conjugate points
Let triangle ![]() and points
and points ![]() and
and ![]() inside it be given.
inside it be given.
Let ![]() be the projections
be the projections ![]() on sides
on sides ![]() respectively.
respectively.
Let ![]() be the projections
be the projections ![]() on sides
on sides ![]() respectively.
respectively.
Let ![]() Prove that point
Prove that point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
One can prove a similar theorem in the case ![]() outside
outside ![]()
Proof
![]()
![]()
Denote ![]()
![]()
![]()
![]()
![]()
![]() Similarly
Similarly ![]() Hence point
Hence point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
vladimir.shelomovskii@gmail.com, vvsss
Circumcircle of pedal triangles
Let ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Let ![]() be the projection
be the projection ![]() on sides
on sides ![]() respectively.
respectively.
Let ![]() be the projection
be the projection ![]() on sides
on sides ![]() respectively.
respectively.
Prove that points ![]() are concyclic.
are concyclic.
The midpoint ![]() is circumcenter of
is circumcenter of ![]()
Proof
Let ![]()
![]()
Hence points ![]() are concyclic.
are concyclic.
![]() is trapezoid,
is trapezoid, ![]()
the midpoint ![]() is circumcenter of
is circumcenter of ![]()
Similarly points ![]() are concyclic and points
are concyclic and points ![]() are concyclic.
are concyclic.
Therefore points ![]() are concyclic, so the midpoint
are concyclic, so the midpoint ![]() is circumcenter of
is circumcenter of ![]()
vladimir.shelomovskii@gmail.com, vvsss
Common circumcircle of the pedal triangles as the sign of isogonally conjugate points
Let triangle ![]() and points
and points ![]() and
and ![]() inside it be given. Let
inside it be given. Let ![]() be the projections
be the projections ![]() on sides
on sides ![]() respectively.
Let
respectively.
Let ![]() be the projections
be the projections ![]() on sides
on sides ![]() respectively.
respectively.
Let points ![]() be concyclic and none of them lies on the sidelines of
be concyclic and none of them lies on the sidelines of ![]()
Then point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
This follows from the uniqueness of the conjugate point and the fact that the line intersects the circle in at most two points.
vladimir.shelomovskii@gmail.com, vvsss
Two pares of isogonally conjugate points
Let triangle ![]() and points
and points ![]() and
and ![]() be given. Let points
be given. Let points ![]() and
and ![]() be the isogonal conjugate of a points
be the isogonal conjugate of a points ![]() and
and ![]() with respect to a triangle
with respect to a triangle ![]() respectively.
respectively.
Let ![]() cross
cross ![]() at
at ![]() and
and ![]() cross
cross ![]() at
at ![]()
Prove that point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to
with respect to ![]()
Proof
There are two pairs of isogonals ![]() and
and ![]() with respect to the angle
with respect to the angle ![]()
![]() are isogonals with respect to the
are isogonals with respect to the ![]() in accordance with The isogonal theorem.
in accordance with The isogonal theorem.
Similarly ![]() are the isogonals with respect to the
are the isogonals with respect to the ![]()
Therefore the point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to
with respect to ![]()
vladimir.shelomovskii@gmail.com, vvsss
Circles
Let ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Let ![]() be the circumcenter of
be the circumcenter of ![]()
Let ![]() be the circumcenter of
be the circumcenter of ![]()
Prove that points ![]() and
and ![]() are inverses with respect to the circumcircle of
are inverses with respect to the circumcircle of ![]()
Proof
The circumcenter of ![]() point
point ![]() and points
and points ![]() and
and ![]() lies on the perpendicular bisector of
lies on the perpendicular bisector of ![]()
![]()
![]()
![]()
![]() Similarly
Similarly ![]()
![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Equidistant isogonal conjugate points
Let triangle ![]() with incenter
with incenter ![]() be given.
Denote
be given.
Denote ![]()
Let point ![]() be the isogonal conjugate of the point
be the isogonal conjugate of the point ![]() with respect to
with respect to ![]()
Prove that ![]() iff
iff ![]()
Proof
1. Let ![]() WLOG,
WLOG, ![]() Point
Point ![]()
Point ![]() is the isogonal conjugate of the point
is the isogonal conjugate of the point ![]() with respect to
with respect to ![]()
![]() So points
So points ![]() and
and ![]() are concyclic.
are concyclic.
Let ![]() Then
Then ![]() is the center of
is the center of ![]()
![]()
![]()
2. Let ![]()
![]()
Points ![]() and
and ![]() are symmetric with respect
are symmetric with respect ![]()
Suppose that ![]()
Let ![]() be the center of
be the center of ![]() be the center of
be the center of ![]()
It is known that points ![]() and
and ![]() are inverted with respect to the circumcircle of
are inverted with respect to the circumcircle of ![]()
Points ![]() and
and ![]() belong to bisector
belong to bisector ![]()
Therefore ![]() divide
divide ![]() and
and ![]()
WLOG (see diagram) ![]() contradiction.
contradiction.
vladimir.shelomovskii@gmail.com, vvsss
Simplified distance formula for isogonal points
Let triangle ![]() points
points ![]() and
and ![]() and
and ![]() be given. Let point
be given. Let point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
![]() Prove that
Prove that ![]()
Proof
![]() and
and ![]() are both subtended by arc
are both subtended by arc ![]()
![]()
![]() Similarly
Similarly ![]() Product of isogonal segments
Product of isogonal segments
vladimir.shelomovskii@gmail.com, vvsss
Point on circumcircle
Let triangle ![]() points
points ![]() and
and ![]() be given.
be given.
Denote ![]()
![]() Prove that
Prove that ![]()
Proof
WLOG, the order of the points is ![]() as shown on diagram.
as shown on diagram.
The spiral symilarity centered at ![]() maps
maps ![]() to
to ![]() and point
and point ![]() to point
to point ![]()
![]() is the external angle of
is the external angle of ![]()
![]()
Corollary
![]() is the isogonal conjugate to
is the isogonal conjugate to ![]() with respect
with respect ![]()
vladimir.shelomovskii@gmail.com, vvsss
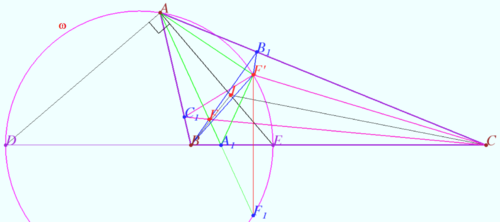
Fixed point on circumcircle
Let triangle ![]() point
point ![]() on circumcircle
on circumcircle ![]() and point
and point ![]() be given.
be given.
Point ![]() lies on
lies on ![]() point
point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Prove that ![]() is fixed point and not depends from position of
is fixed point and not depends from position of ![]()
Proof
WLOG, the order of points on sideline is ![]() point
point ![]() is closer to
is closer to ![]() than to
than to ![]()
Denote ![]()
![]()
Spiral similarity centered at ![]() which maps
which maps ![]() into
into ![]() transform point
transform point ![]() into point
into point ![]()
![]()
![]() Points
Points ![]() and
and ![]() are collinear.
are collinear.
It is known ( Ratio of isogonal segments) that ![]()
We use the ratio of the areas and get:
![]()
![]()
![]() Denote
Denote ![]()
![]()
![]()
![]() Therefore
Therefore ![]() which means ( Problems | Simple) that
which means ( Problems | Simple) that ![]() is the radical axes of
is the radical axes of ![]() and
and ![]()
![]() and not depends from position of
and not depends from position of ![]()
vladimir.shelomovskii@gmail.com, vvsss
Distance formula for isogonal points
Let triangle ![]() and point
and point ![]() be given.
be given.
Let point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Let lines ![]() and
and ![]() cross sideline
cross sideline ![]() at
at ![]() and
and ![]() and circumcircle of
and circumcircle of ![]() at
at ![]() and
and ![]() respectively.
respectively.
We apply the Isogonal’s property and get ![]()
![]() We apply the Ptolemy's theorem to
We apply the Ptolemy's theorem to ![]() and get
and get ![]()
We apply the barycentric coordinates and get
![]()
vladimir.shelomovskii@gmail.com, vvsss
Miquel point for isogonal conjugate points
Let triangle ![]() points
points ![]() and
and ![]() be given. Let point
be given. Let point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
![]() Let
Let ![]() be the Miquel point of a complete quadrilateral
be the Miquel point of a complete quadrilateral ![]()
Prove that ![]() lies on the circumcircle of
lies on the circumcircle of ![]()
Proof
Point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]() so point
so point ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Points ![]() and
and ![]() lies on the same line, therefore
lies on the same line, therefore ![]()
![]() Point
Point ![]() lies on circles
lies on circles ![]() and
and ![]() spiral similarity centered at
spiral similarity centered at ![]() transform triangle
transform triangle ![]() to
to ![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Point on circumcircle
Let triangle ![]() and points
and points ![]() and
and ![]() be given.
be given.
Let ![]()
Let lines ![]() and
and ![]() be the isogonals with respect to the angle
be the isogonals with respect to the angle ![]()
Let ![]() be an arbitrary point on
be an arbitrary point on ![]()
Prove that ![]() lies on
lies on ![]()
Simplified problem
Let ![]() and points
and points ![]() and
and ![]() be given,
be given, ![]()
Let lines ![]() and
and ![]() be the isogonals with respect to
be the isogonals with respect to ![]()
Prove that ![]()
Proof, Simplified problem
![]()
![]()
![]()
![]()
points ![]() are concyclic on
are concyclic on ![]()
Proof
Let points ![]() and
and ![]() be the isogonal conjugate of a points
be the isogonal conjugate of a points ![]() and
and ![]() with respect to a triangle
with respect to a triangle ![]()
It is known that ![]()
![]()
![]()
![]()
![]() points
points ![]() are concyclic on
are concyclic on ![]()
vladimir.shelomovskii@gmail.com, vvsss
Isogonal of line BC with respect to angle BAC
Let triangle ![]() be given,
be given, ![]()
Let lines ![]() and
and ![]() be the isogonals with respect to
be the isogonals with respect to ![]()
Prove that ![]() is tangent to
is tangent to ![]()
Proof
Let ![]() and
and ![]() be the circumcenter and the orthocenter of
be the circumcenter and the orthocenter of ![]() respectively.
respectively.
![]()
![]() is isogonal to
is isogonal to ![]() with respect to
with respect to ![]() is tangent to
is tangent to ![]()
vladimir.shelomovskii@gmail.com, vvsss
Isogonal bijection lines and points
Let triangle ![]() and line
and line ![]() be given,
be given, ![]()
Define ![]() the point with property
the point with property ![]()
Prove that ![]() is equal the angle
is equal the angle ![]() between
between ![]() and
and ![]()
Proof
WLOG, the configuration is the same as shown on diagram, ![]() is the tangent to
is the tangent to ![]()
![]() is isogonal to
is isogonal to ![]() is isogonal to
is isogonal to ![]() with respect to
with respect to ![]()
![]() A bijection has been established between the set of lines parallel to a given one and the set of points of the circumcircle.
A bijection has been established between the set of lines parallel to a given one and the set of points of the circumcircle.
vladimir.shelomovskii@gmail.com, vvsss
Miquel point for two pare isogonal points
Let triangle ![]() and points
and points ![]() and
and ![]() be given.
be given.
Let points ![]() and
and ![]() be the isogonal conjugate of the points
be the isogonal conjugate of the points ![]() and
and ![]() with respect to
with respect to ![]() is the Miquel point of quadrilateral
is the Miquel point of quadrilateral ![]()
Prove that ![]()
Proof
Denote ![]()
Then ![]() is the Miquel point of quadrilateral
is the Miquel point of quadrilateral ![]()
Denote ![]()
Let ![]() be the point with property
be the point with property ![]()
WLOG, configuration is similar as shown in diagram.
![]() ( Isogonal_bijection_lines_and_points).
( Isogonal_bijection_lines_and_points).
![]()
vladimir.shelomovskii@gmail.com, vvsss
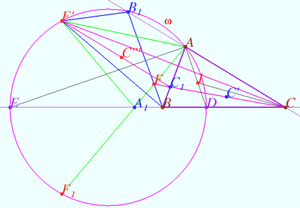
Isogonic center’s conjugate point
Let triangle ![]() with isogonic center
with isogonic center ![]() or
or ![]() be given. Denote
be given. Denote ![]()
Let line ![]() be the axial symmetry of line
be the axial symmetry of line ![]() according to the sideline
according to the sideline ![]()
Define lines ![]() and
and ![]() similarly.
similarly.
Prove that the lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Let ![]() be the incenter of
be the incenter of ![]()
![]() Let
Let ![]() is simmetric to
is simmetric to ![]() with respect
with respect ![]()
The diameter ![]() of
of ![]() lies on
lies on ![]()
Therefore ![]() is the isogonal conjugate of
is the isogonal conjugate of ![]() with respect to
with respect to ![]()
Similarly ![]() and
and ![]() are the isogonal conjugate of
are the isogonal conjugate of ![]() and
and ![]() so point
so point ![]() is the isogonal conjugate of point
is the isogonal conjugate of point ![]() with respect to
with respect to ![]()
The second diagram show construction in the case ![]() The proof is similar.
The proof is similar.
vladimir.shelomovskii@gmail.com, vvsss
Three pairs isogonal points
Let a triangle ![]() points
points ![]() and
and ![]() be given,
be given, ![]() Points
Points ![]() and
and ![]() are the isogonal conjugate of the points
are the isogonal conjugate of the points ![]() and
and ![]() respectively, with respect to
respectively, with respect to ![]()
Prove that ![]()
Proof
Denote ![]()
![]() We use isogonal properties and get
We use isogonal properties and get
![]() By applying the Law of Sines, we get
By applying the Law of Sines, we get ![]() Symilarly,
Symilarly, ![]() We multiply these equations and get
We multiply these equations and get
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Ratio for three pairs of isogonal points
Let a triangle ![]() points
points ![]() and
and ![]() be given,
be given, ![]()
Points ![]() and
and ![]() are the isogonal conjugate of the points
are the isogonal conjugate of the points ![]() and
and ![]() respectively, with respect to
respectively, with respect to ![]()
Denote ![]() and
and ![]() the circumradii of triangles
the circumradii of triangles ![]() and
and ![]() respectively.
respectively.
Prove that ![]()
Proof
Denote ![]()
![]() where
where ![]() is the area of the figure
is the area of the figure ![]()
![]() Similarly,
Similarly, ![]()
![]()
![]()
![]()
![]() Similarly,
Similarly, ![]() It is known that
It is known that ![]() ( Three pairs isogonal points), therefore
( Three pairs isogonal points), therefore
![]() Comment: The main idea of the proof was found by Leonid Shatunov.
Comment: The main idea of the proof was found by Leonid Shatunov.
vladimir.shelomovskii@gmail.com, vvsss
Problems
- Given a nonisosceles, nonright triangle
 let
let  denote the center of its circumscribed circle, and let
denote the center of its circumscribed circle, and let  and
and  be the midpoints of sides
be the midpoints of sides  and
and  respectively. Point
respectively. Point  is located on the ray
is located on the ray  so that
so that  is similar to
is similar to  . Points
. Points  and
and  on rays
on rays  and
and  respectively, are defined similarly. Prove that lines
respectively, are defined similarly. Prove that lines  and
and  are concurrent. (Source)
are concurrent. (Source)
- Let
 be a given point inside quadrilateral
be a given point inside quadrilateral  . Points
. Points  and
and  are located within
are located within  such that
such that  ,
,  ,
,  ,
,  . Prove that
. Prove that  if and only if
if and only if  . (Source)
. (Source)
- Let
 and
and  be the bisectors of a triangle
be the bisectors of a triangle 
- The segments
 and
and  meet at point
meet at point  Let
Let  be the projection of
be the projection of  to
to 
- Points
 and
and  on the sides
on the sides  and
and  respectively, are such that
respectively, are such that 
- Prove that
 (Source)
(Source)
- IMO 2007 Short list/G3
The diagonals of a trapezoid ![]() intersect at point
intersect at point ![]()
Point ![]() lies between the parallel lines
lies between the parallel lines ![]() and
and ![]() such that
such that ![]() and line
and line ![]() separates points
separates points ![]() and
and ![]()
Prove that ![]()
Proof
![]()
![]() and
and ![]() are isogonals with respect
are isogonals with respect ![]()
![]()
![]() is isogonal to
is isogonal to ![]() with respect
with respect ![]()
From the converse of The isogonal theorem we get
![]()
vladimir.shelomovskii@gmail.com, vvsss This article is a stub. Help us out by expanding it.