Difference between revisions of "Angle bisector"
(add external angle bisectors) |
|||
| Line 58: | Line 58: | ||
dot("I",I,(-1,2)); | dot("I",I,(-1,2)); | ||
draw(circle(I,length(I-foot(I,X,Y))),blue); | draw(circle(I,length(I-foot(I,X,Y))),blue); | ||
| − | markangle(n=1, | + | markangle(n=1,3*(Z-X)+X,Z,exX,radius=22,marker(markinterval(stickframe(n=3),true))); |
| − | + | markangle(n=1,exX,Z,Y,radius=20,marker(markinterval(stickframe(n=3),true))); | |
| + | markangle(n=1,3*(Y-Z)+Z,Y,exZ,radius=22,marker(markinterval(stickframe(n=2),true))); | ||
| + | markangle(n=1,exZ,Y,X,radius=20,marker(markinterval(stickframe(n=2),true))); | ||
| + | markangle(n=1,3*(X-Y)+Y,X,exY,radius=22,marker(markinterval(stickframe(n=1),true))); | ||
| + | markangle(n=1,exY,X,Z,radius=20,marker(markinterval(stickframe(n=1),true))); | ||
| − | + | markangle(n=3,I,Z,X,radius=20); | |
| + | markangle(n=3,Y,Z,I,radius=22); | ||
| + | markangle(n=2,Z,X,I,radius=20); | ||
| + | markangle(n=2,I,X,Y,radius=22); | ||
| + | markangle(n=1,X,Y,I,radius=22); | ||
| + | markangle(n=1,I,Y,Z,radius=20); | ||
| + | </asy>|center|Triangle <math>\triangle XYZ</math> with [[incenter]] ''I'', [[incircle]] (blue), [[angle bisector]]s (orange), and [[angle bisector|external angle bisectors]] (green)}} | ||
==See also== | ==See also== | ||
| Line 68: | Line 78: | ||
* [[Stewart's Theorem]] | * [[Stewart's Theorem]] | ||
| − | |||
[[Category:Geometry]] | [[Category:Geometry]] | ||
Revision as of 02:00, 1 July 2020
| This is an AoPSWiki Word of the Week for June 6-12 |
For an angle 
, the (internal) angle bisector of is the line from B such that the angle between this line and 
is congruent to the angle between this line and 
:
A given angle also has an external angle bisector, which bisects external angle 
:
![[asy] import markers; pair A,B,C,D,E,F; B=(0,0); C=(5,0); A=(4,2); D=(3,4); E=(10/3,0); F=rotate(-90,A)*(E); draw(A--B--C--cycle,blue); draw(C--D,blue); pen p=blue+0.15mm; draw(A--F,p); dot(A^^B^^C,red); label("$A$",A,NE); label("$B$",B,W); label("$C$",C,E); markangle(n=1,radius=20,D,A,F,green); markangle(n=1,radius=22,F,A,B,green); [/asy]](http://latex.artofproblemsolving.com/2/f/5/2f50679988883833282611240be251280d884bc4.png)
The external angle is defined by 
, and the two angle bisectors are perpendicular to each other.
Features of Angle Bisectors
- The distances from a point on an angle bisector to both of its sides are equal.
- The angle bisectors are the locus of points which are equidistant from the two sides of the angle.
- A reflection about either angle bisector maps the two sides of the angle to each other.
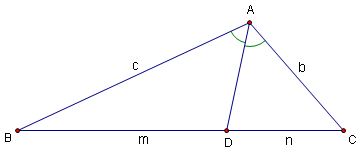
- In a triangle, the Angle Bisector Theorem gives the ratio in which the angle bisector cuts the opposite side.
- In a triangle, the internal angle bisectors (which are cevians) all intersect at the incenter of the triangle. The internal angle bisector of one angle and the external angle bisectors of the other two angles all intersect at an excenter of the triangle.
- A bisector of an angle can be constructed using a compass and straightedge.
|
|
  with incenter I, incircle (blue), angle bisectors (orange), and external angle bisectors (green)
|
![[asy] size(300); import markers; pair excenter(pair A, pair B, pair C){ pair X, Z; X=A+expi((angle(A-B)+angle(C-A))/2); Z=C+expi((angle(C-B)+angle(A-C))/2); return extension(X,A,Z,C); } pair X=(0,0), Y=(-10,0), Z=(-3,6); pair exX=excenter(Z,X,Y), exY=excenter(X,Y,Z), exZ=excenter(Y,Z,X); label("X",X,2*(1.5,-1));label("Y",Y,2*(-3,-1));label("Z",Z,(0.6,2)); dot(X^^Y^^Z); draw(0.3*(X-Y)+X--Y+0.3*(Y-X));draw(0.3*(Y-Z)+Y--Z+0.3*(Z-Y));draw(0.3*(X-Z)+X--Z+0.3*(Z-X)); draw(X+0.3*(X-exX)--exX,orange);draw(Y+0.3*(Y-exY)--exY,orange);draw(Z+0.3*(Z-exZ)--0.6*(exZ-Z)+Z,orange); draw(Y-0.5*(exX-Y)--Y+0.5*(exX-Y),green);draw(Z-0.5*(exX-Z)--Z+0.5*(exX-Z),green);draw(X-0.5*(exY-X)--X+0.5*(exY-X),green); pair I=extension(X,exX,Z,exZ); dot("I",I,(-1,2)); draw(circle(I,length(I-foot(I,X,Y))),blue); markangle(n=1,3*(Z-X)+X,Z,exX,radius=22,marker(markinterval(stickframe(n=3),true))); markangle(n=1,exX,Z,Y,radius=20,marker(markinterval(stickframe(n=3),true))); markangle(n=1,3*(Y-Z)+Z,Y,exZ,radius=22,marker(markinterval(stickframe(n=2),true))); markangle(n=1,exZ,Y,X,radius=20,marker(markinterval(stickframe(n=2),true))); markangle(n=1,3*(X-Y)+Y,X,exY,radius=22,marker(markinterval(stickframe(n=1),true))); markangle(n=1,exY,X,Z,radius=20,marker(markinterval(stickframe(n=1),true))); markangle(n=3,I,Z,X,radius=20); markangle(n=3,Y,Z,I,radius=22); markangle(n=2,Z,X,I,radius=20); markangle(n=2,I,X,Y,radius=22); markangle(n=1,X,Y,I,radius=22); markangle(n=1,I,Y,Z,radius=20); [/asy]](http://latex.artofproblemsolving.com/1/b/e/1be1fa15a3cd0653bc980757a6211e8f148e5daf.png)
