Difference between revisions of "2006 AMC 12A Problems/Problem 13"

Revision as of 18:19, 2 February 2007

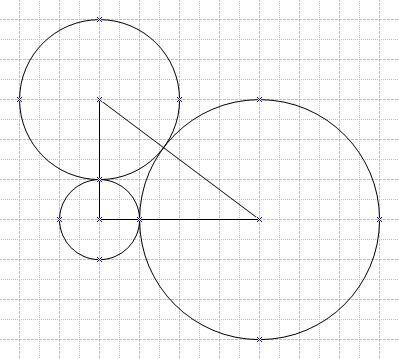
Problem

The vertices of a $3-4-5$ right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?

$\mathrm{(A) \ } 12\pi\qquad \mathrm{(B) \ } \frac{25\pi}{2}\qquad \mathrm{(C) \ } 13\pi\qquad \mathrm{(D) \ } \frac{27\pi}{2}\qquad\mathrm{(E) \ } 14\pi$

Solution

Let the radius of the smallest circle be $a$ . We find that the radius of the largest circle is $4-a$ and the radius of the second largest circle is $3-a$ . Thus, $4-a+3-a=5\iff a=1$ . The radii of the other circles are $3$ and $2$ . The sum of their areas is $\pi+9\pi+4\pi=14\pi\iff\mathrm{(E)}$

2006 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

@@ Line 14: / Line 14: @@
 * [[2006 AMC 12A Problems]]
-{{AMC box|year=2006|n=12A|num-b=13|num-a=15}}
+{{AMC12 box|year=2006|ab=A|num-b=12|num-a=14}}
 [[Category:Introductory Geometry Problems]]

Page

Toolbox

Search

Difference between revisions of "2006 AMC 12A Problems/Problem 13"

Revision as of 18:19, 2 February 2007

Problem

Solution

See also