Difference between revisions of "2007 USAMO Problems/Problem 4"
(→Solution) |
(images to come) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
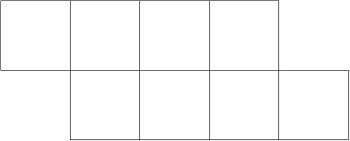
| + | An ''animal'' with <math>n</math> ''cells'' is a connected figure consisting of <math>n</math> equal-sized [[square]] cells.<math>{}^1</math> The figure below shows an 8-cell animal. | ||
| − | + | <div style="text-align:center;">[[Image:2007 USAMO-4.PNG|350px]]</div> | |
| − | + | A ''dinosaur'' is an animal with at least 2007 cells. It is said to be ''primitive'' it its cells cannot be partitioned into two or more dinosaurs. Find with proof the [[maximum]] number of cells in a primitive dinosaur. | |
| − | + | <small><math>{}^1</math>Animals are also called ''[[polyomino]]es''. They can be defined [[induction|inductively]]. Two cells are ''adjacent'' if they share a complete [[edge]]. A single cell is an animal, and given an animal with <math>n</math> cells, one with <math>n+1</math> cells is obtained by adjoining a new cell by making it adjacent to one or more existing cells.</small> | |
| − | + | __TOC__ | |
| + | == Solution == | ||
| + | === Solution 1 === | ||
| + | Let a <math>n</math>-dino denote an animal with <math>n</math> or more cells. | ||
| − | + | We show by [[induction]] that an <math>n</math>-dino with <math>4n-2</math> or more animal cells is not primitive. (Note: if it had more, we could just take off enough until it had 4n-2, which would have a partition, and then add the cells back on) | |
| − | |||
| − | + | Base Case: If <math>\displaystyle n=1</math>, we have two boxes, which are clearly not primitive. | |
| − | + | Inductive Step: Assume any <math>4n-2</math> cell animal can be partitioned into two or more <math>n</math>-dinos. | |
| − | + | For a given <math>4n+2</math>-dino, take off any four cells (call them <math>w,\ x,\ y,\ z</math>) to get an animal with <math>4n-2</math> cells. | |
| − | + | This can be partitioned into two or more <math>n</math>-dinos, let's call them <math>A</math> and <math>B</math>. This means that <math>A:B</math>, where : denotes a connection. | |
| − | + | If both <math>A</math> and <math>B</math> are <math>n+1</math>-dinos or if <math>w,\ x,\ y,\ z</math> don't all attach to one of them, then we're done. | |
| − | + | So assume <math>A</math> has <math>n</math> cells and thus <math>B</math> has at least <math>3n-2</math> cells, and that <math>w,\ x,\ y,\ z</math> are added to <math>B</math>. So <math>B</math> has <math>3n+2</math> cells total. | |
| − | + | Let <math>C</math> denote the cell of <math>B</math> attached to <math>A</math>. There are <math>3n+1</math> cells on <math>B</math> besides <math>C</math>. Thus, of the three sides of <math>C</math> not attached to <math>A</math>, one of them must have <math>n+1</math> cells by the [[pigeonhole principle]]. It then follows that we can add <math>A</math>, <math>C</math>, and the other two sides together to get an <math>n+1</math> dino, and the side of <math>C</math> that has <math>n+1</math> cells is also an n-dino, so we can partition the animal with <math>4n+2</math> cells into two <math>n+1</math>-dinos and we're done. | |
| − | + | Thus, our answer is <math>\displaystyle 4(2006) + 1 = 8025</math> cells. | |
| − | + | === Solution 2 === | |
| − | |||
| − | |||
| − | |||
| − | == Solution 2 == | ||
For simplicity, let <math>k=2007</math> and let <math>n</math> be the number of squares. Let the centers of the squares be verticies, and connect any centers of adjacent squares with edges. Suppose we have some loops. Just remove an edge in the loop. We are still connected since you can go around the other way in the loop. Now we have no loops. Each vertex can have at most 4 edges coming out of it. For each point, assign it the quadruple: <math>(a,b,c,d)</math> where <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math> are the numbers of verticies on each branch, wlog <math>a\ge b\ge c\ge d</math>. Note <math>a+b+c+d=n-1</math>. | For simplicity, let <math>k=2007</math> and let <math>n</math> be the number of squares. Let the centers of the squares be verticies, and connect any centers of adjacent squares with edges. Suppose we have some loops. Just remove an edge in the loop. We are still connected since you can go around the other way in the loop. Now we have no loops. Each vertex can have at most 4 edges coming out of it. For each point, assign it the quadruple: <math>(a,b,c,d)</math> where <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math> are the numbers of verticies on each branch, wlog <math>a\ge b\ge c\ge d</math>. Note <math>a+b+c+d=n-1</math>. | ||
| Line 50: | Line 49: | ||
So <math>k=2007</math>: <math>4*2007-3=8025</math>. | So <math>k=2007</math>: <math>4*2007-3=8025</math>. | ||
| − | + | == See also == | |
| − | |||
| − | |||
| − | |||
{{USAMO newbox|year=2007|num-b=3|num-a=5}} | {{USAMO newbox|year=2007|num-b=3|num-a=5}} | ||
Revision as of 16:09, 26 April 2007
Problem
An animal with ![]() cells is a connected figure consisting of
cells is a connected figure consisting of ![]() equal-sized square cells.
equal-sized square cells.![]() The figure below shows an 8-cell animal.
The figure below shows an 8-cell animal.
A dinosaur is an animal with at least 2007 cells. It is said to be primitive it its cells cannot be partitioned into two or more dinosaurs. Find with proof the maximum number of cells in a primitive dinosaur.
![]() Animals are also called polyominoes. They can be defined inductively. Two cells are adjacent if they share a complete edge. A single cell is an animal, and given an animal with
Animals are also called polyominoes. They can be defined inductively. Two cells are adjacent if they share a complete edge. A single cell is an animal, and given an animal with ![]() cells, one with
cells, one with ![]() cells is obtained by adjoining a new cell by making it adjacent to one or more existing cells.
cells is obtained by adjoining a new cell by making it adjacent to one or more existing cells.
Contents
[hide]Solution
Solution 1
Let a ![]() -dino denote an animal with
-dino denote an animal with ![]() or more cells.
or more cells.
We show by induction that an ![]() -dino with
-dino with ![]() or more animal cells is not primitive. (Note: if it had more, we could just take off enough until it had 4n-2, which would have a partition, and then add the cells back on)
or more animal cells is not primitive. (Note: if it had more, we could just take off enough until it had 4n-2, which would have a partition, and then add the cells back on)
Base Case: If ![]() , we have two boxes, which are clearly not primitive.
, we have two boxes, which are clearly not primitive.
Inductive Step: Assume any ![]() cell animal can be partitioned into two or more
cell animal can be partitioned into two or more ![]() -dinos.
-dinos.
For a given ![]() -dino, take off any four cells (call them
-dino, take off any four cells (call them ![]() ) to get an animal with
) to get an animal with ![]() cells.
cells.
This can be partitioned into two or more ![]() -dinos, let's call them
-dinos, let's call them ![]() and
and ![]() . This means that
. This means that ![]() , where : denotes a connection.
, where : denotes a connection.
If both ![]() and
and ![]() are
are ![]() -dinos or if
-dinos or if ![]() don't all attach to one of them, then we're done.
don't all attach to one of them, then we're done.
So assume ![]() has
has ![]() cells and thus
cells and thus ![]() has at least
has at least ![]() cells, and that
cells, and that ![]() are added to
are added to ![]() . So
. So ![]() has
has ![]() cells total.
cells total.
Let ![]() denote the cell of
denote the cell of ![]() attached to
attached to ![]() . There are
. There are ![]() cells on
cells on ![]() besides
besides ![]() . Thus, of the three sides of
. Thus, of the three sides of ![]() not attached to
not attached to ![]() , one of them must have
, one of them must have ![]() cells by the pigeonhole principle. It then follows that we can add
cells by the pigeonhole principle. It then follows that we can add ![]() ,
, ![]() , and the other two sides together to get an
, and the other two sides together to get an ![]() dino, and the side of
dino, and the side of ![]() that has
that has ![]() cells is also an n-dino, so we can partition the animal with
cells is also an n-dino, so we can partition the animal with ![]() cells into two
cells into two ![]() -dinos and we're done.
-dinos and we're done.
Thus, our answer is ![]() cells.
cells.
Solution 2
For simplicity, let ![]() and let
and let ![]() be the number of squares. Let the centers of the squares be verticies, and connect any centers of adjacent squares with edges. Suppose we have some loops. Just remove an edge in the loop. We are still connected since you can go around the other way in the loop. Now we have no loops. Each vertex can have at most 4 edges coming out of it. For each point, assign it the quadruple:
be the number of squares. Let the centers of the squares be verticies, and connect any centers of adjacent squares with edges. Suppose we have some loops. Just remove an edge in the loop. We are still connected since you can go around the other way in the loop. Now we have no loops. Each vertex can have at most 4 edges coming out of it. For each point, assign it the quadruple: ![]() where
where ![]() ,
, ![]() ,
, ![]() ,
, ![]() are the numbers of verticies on each branch, wlog
are the numbers of verticies on each branch, wlog ![]() . Note
. Note ![]() .
.
Claim: If ![]() , then we must be able to divide the animal into two dinosaurs.
Chose a vertex,
, then we must be able to divide the animal into two dinosaurs.
Chose a vertex, ![]() , for which
, for which ![]() is minimal (i.e. out of all maximal elements in a quadruple, choose the one with the least maximal element). We have that
is minimal (i.e. out of all maximal elements in a quadruple, choose the one with the least maximal element). We have that ![]() , so
, so ![]() . Hence we can just cut off that branch, that forms a dinosaur.
. Hence we can just cut off that branch, that forms a dinosaur.
But suppose the remaining verticies do not make a dinosaur. Then we have ![]() . Now move to the first point on the branch at
. Now move to the first point on the branch at ![]() . We have a new quadruple p,q,r,b+c+d+1) where
. We have a new quadruple p,q,r,b+c+d+1) where ![]() .
.
Now consider the maximal element of that quadruple. We already have ![]() . WLOG
. WLOG ![]() , then
, then ![]() so
so ![]() , so
, so ![]() is the maximal element of that quadruple.
is the maximal element of that quadruple.
Also ![]() , so
, so ![]() . But that is a contradiction to the minimality of
. But that is a contradiction to the minimality of ![]() . Therefore, we must have that
. Therefore, we must have that ![]() , so we have a partition of two dinosaurs.
, so we have a partition of two dinosaurs.
Maximum: ![]() .
Consider a cross with each branch having
.
Consider a cross with each branch having ![]() verticies. Clearly if we take partition
verticies. Clearly if we take partition ![]() verticies, we remove the center, and we are not connected.
verticies, we remove the center, and we are not connected.
So ![]() :
: ![]() .
.
See also
| 2007 USAMO (Problems • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||