Difference between revisions of "2021 JMPSC Accuracy Problems/Problem 12"
(→Solution) |
|||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 13: | Line 13: | ||
Since <math>EF</math> is parallel to <math>AC</math> and <math>\angle C =60^\circ</math>, we have that <math>\angle BFE = 60^\circ</math> by corresponding angles. Similarly, <math>\angle BEF = 90^\circ</math> and it follows that <math>\triangle BFE</math> is a <math>30-60-90</math> right triangle. | Since <math>EF</math> is parallel to <math>AC</math> and <math>\angle C =60^\circ</math>, we have that <math>\angle BFE = 60^\circ</math> by corresponding angles. Similarly, <math>\angle BEF = 90^\circ</math> and it follows that <math>\triangle BFE</math> is a <math>30-60-90</math> right triangle. | ||
| − | Since the side opposite the <math>60^\circ</math> angle in <math>\triangle BFE</math> is <math>1</math>, we use our <math>30-60-90</math> ratios to find that <math>EF=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}.</math> In rectangle <math>EFDA</math>, we also have <cmath>AD=\frac{\sqrt{3}}{3}.</cmath> Analogously, we find that <cmath>QP=\frac{\sqrt{3}}{3}.</cmath> Since we are looking for the base <math>d</math> of the horizontal rectangle and we are given <cmath>PA=1,</cmath> we have <cmath>d=QP+PA+AD=\frac{\sqrt{3}}{3}+1+\frac{\sqrt{3}}{3}=\frac{3+2\sqrt{3}}{3}.</cmath> This gives us an answer of <math>2+3=\boxed{8}.</math> ~ samrocksnature | + | Since the side opposite the <math>60^\circ</math> angle in <math>\triangle BFE</math> is <math>1</math>, we use our <math>30-60-90</math> ratios to find that <math>EF=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}.</math> In rectangle <math>EFDA</math>, we also have <cmath>AD=\frac{\sqrt{3}}{3}.</cmath> Analogously, we find that <cmath>QP=\frac{\sqrt{3}}{3}.</cmath> Since we are looking for the base <math>d</math> of the horizontal rectangle and we are given <cmath>PA=1,</cmath> we have <cmath>d=QP+PA+AD=\frac{\sqrt{3}}{3}+1+\frac{\sqrt{3}}{3}=\frac{3+2\sqrt{3}}{3}.</cmath> This gives us an answer of <math>2+3+3=\boxed{8}.</math> ~ samrocksnature |
| + | |||
| + | ==Solution 2== | ||
| + | Since the angles of an equilateral triangle are <math>60^o</math>, we have by similar triangles that the length of the segments of the "small" rectangles are <math>\frac{\sqrt{3}}{3}</math>, meaning the answer is <math>\frac{3+2\sqrt{3}}{3} \implies 3+2+3=\boxed{8}</math> | ||
| + | <math>\linebreak</math> | ||
| + | ~Geometry285 | ||
| + | |||
| + | |||
| + | |||
| + | ==See also== | ||
| + | #[[2021 JMPSC Accuracy Problems|Other 2021 JMPSC Accuracy Problems]] | ||
| + | #[[2021 JMPSC Accuracy Answer Key|2021 JMPSC Accuracy Answer Key]] | ||
| + | #[[JMPSC Problems and Solutions|All JMPSC Problems and Solutions]] | ||
| + | {{JMPSC Notice}} | ||
Latest revision as of 16:24, 11 July 2021
Contents
[hide]Problem
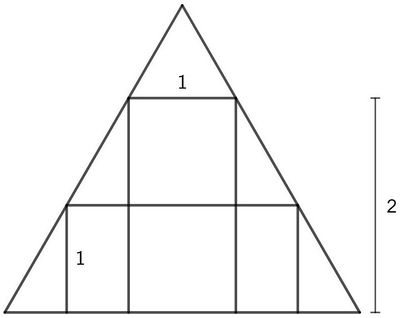
A rectangle with base ![]() and height
and height ![]() is inscribed in an equilateral triangle. Another rectangle with height
is inscribed in an equilateral triangle. Another rectangle with height ![]() is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction
is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction ![]() such that
such that ![]() Find
Find ![]() .
.
Solution
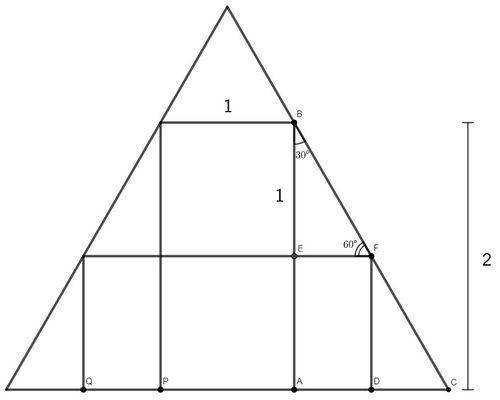
We are given ![]() , from which in rectangle
, from which in rectangle ![]() we can conclude
we can conclude ![]() . Since
. Since ![]() , we have
, we have ![]()
Since ![]() is parallel to
is parallel to ![]() and
and ![]() , we have that
, we have that ![]() by corresponding angles. Similarly,
by corresponding angles. Similarly, ![]() and it follows that
and it follows that ![]() is a
is a ![]() right triangle.
right triangle.
Since the side opposite the ![]() angle in
angle in ![]() is
is ![]() , we use our
, we use our ![]() ratios to find that
ratios to find that ![]() In rectangle
In rectangle ![]() , we also have
, we also have ![]() Analogously, we find that
Analogously, we find that ![]() Since we are looking for the base
Since we are looking for the base ![]() of the horizontal rectangle and we are given
of the horizontal rectangle and we are given ![]() we have
we have ![]() This gives us an answer of
This gives us an answer of ![]() ~ samrocksnature
~ samrocksnature
Solution 2
Since the angles of an equilateral triangle are ![]() , we have by similar triangles that the length of the segments of the "small" rectangles are
, we have by similar triangles that the length of the segments of the "small" rectangles are ![]() , meaning the answer is
, meaning the answer is ![]()
![]() ~Geometry285
~Geometry285
See also
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.