Difference between revisions of "2016 USAMO Problems/Problem 3"
(→Solution) |
(→Solution) |
||
| Line 11: | Line 11: | ||
{{MAA Notice}} | {{MAA Notice}} | ||
| + | |||
| + | ==Solution 2== | ||
| + | [[File:2016 USAMO 3a.png|300px|right]] | ||
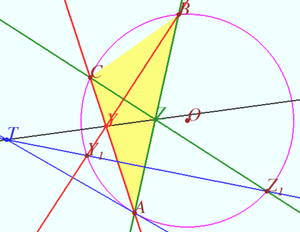
| + | We find point <math>T</math> on line <math>YZ,</math> we prove that <math>TY \perp OI_A</math> and state that <math>P</math> is the point <math>X(24)</math> from ENCYCLOPEDIA OF TRIANGLE, therefore <math>P \in OI_A.</math> | ||
| + | |||
| + | Let <math>\omega</math> be circumcircle of <math>\triangle ABC</math> centered at <math>O.</math> | ||
| + | Let <math>Y_1,</math> and <math>Z_1</math> be crosspoints of <math>\omega</math> and <math>BY,</math> and <math>CZ,</math> respectively. | ||
| + | Let <math>T</math> be crosspoint of <math>YZ</math> and <math>Y_1 Z_1.</math> | ||
| + | In accordance the Pascal theorem for pentagon <math>AZ_1BCY_1,</math> <math>AT</math> is tangent to <math>\omega</math> at <math>A.</math> | ||
==See also== | ==See also== | ||
{{USAMO newbox|year=2016|num-b=2|num-a=4}} | {{USAMO newbox|year=2016|num-b=2|num-a=4}} | ||
Revision as of 15:32, 2 October 2022
Contents
[hide]Problem
Let ![]() be an acute triangle, and let
be an acute triangle, and let ![]() and
and ![]() denote its
denote its ![]() -excenter,
-excenter, ![]() -excenter, and circumcenter, respectively. Points
-excenter, and circumcenter, respectively. Points ![]() and
and ![]() are selected on
are selected on ![]() such that
such that ![]() and
and ![]() Similarly, points
Similarly, points ![]() and
and ![]() are selected on
are selected on ![]() such that
such that ![]() and
and ![]()
Lines ![]() and
and ![]() meet at
meet at ![]() Prove that
Prove that ![]() and
and ![]() are perpendicular.
are perpendicular.
Solution
This problem can be proved in the following two steps.
1. Let ![]() be the
be the ![]() -excenter, then
-excenter, then ![]() and
and ![]() are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for
are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for ![]()
2. Show that ![]() which implies
which implies ![]() This can be proved by multiple applications of the Pythagorean Thm.
This can be proved by multiple applications of the Pythagorean Thm.
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()
Solution 2
We find point ![]() on line
on line ![]() we prove that
we prove that ![]() and state that
and state that ![]() is the point
is the point ![]() from ENCYCLOPEDIA OF TRIANGLE, therefore
from ENCYCLOPEDIA OF TRIANGLE, therefore ![]()
Let ![]() be circumcircle of
be circumcircle of ![]() centered at
centered at ![]() Let
Let ![]() and
and ![]() be crosspoints of
be crosspoints of ![]() and
and ![]() and
and ![]() respectively.
Let
respectively.
Let ![]() be crosspoint of
be crosspoint of ![]() and
and ![]() In accordance the Pascal theorem for pentagon
In accordance the Pascal theorem for pentagon ![]()
![]() is tangent to
is tangent to ![]() at
at ![]()
See also
| 2016 USAMO (Problems • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||