Difference between revisions of "2016 USAMO Problems/Problem 3"
(→Solution 2) |
(→Solution 2) |
||
| Line 104: | Line 104: | ||
[[File:2016 3 Lemma.png|400px|right]] | [[File:2016 3 Lemma.png|400px|right]] | ||
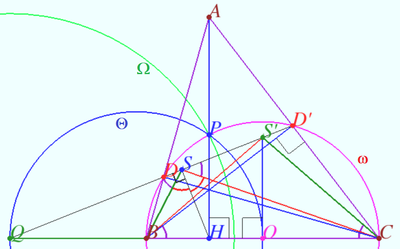
Let <math>\triangle ABC</math> be an acute triangle, and let <math>AH, BD',</math> and <math>CD</math> denote its altitudes. Lines <math>DD'</math> and <math>BC</math> meet at <math>Q, HS \perp DD'.</math> Prove that <math>\angle BSH = \angle CSH.</math> | Let <math>\triangle ABC</math> be an acute triangle, and let <math>AH, BD',</math> and <math>CD</math> denote its altitudes. Lines <math>DD'</math> and <math>BC</math> meet at <math>Q, HS \perp DD'.</math> Prove that <math>\angle BSH = \angle CSH.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>\omega</math> be the circle <math>BCD'D</math> centered at <math>O (O</math> is midpoint <math>BC).</math> | ||
| + | |||
| + | Let <math>\omega</math> meet <math>AH</math> at <math>P.</math> | ||
| + | Let <math>\Omega</math> be the circle centered at <math>Q</math> with radius <math>QP.</math> | ||
| + | |||
| + | Let <math>\Theta</math> be the circle with diameter <math>OQ.</math> | ||
| + | |||
| + | We know that <math>OB = OP = OC = R, PH^2 = R^2 – OH^2 \implies</math> | ||
| + | <math>QP^2 + R^2 = (QH+ HO)^2 \implies P \in \Theta, \Omega \perp \omega.</math> | ||
| + | |||
| + | Let <math>I_{\Omega}</math> be inversion with respect <math>\Omega, I_{\Omega}(B) = C.</math> | ||
| + | |||
| + | Denote <math>I_{\Omega}(D) = D', I_{\Omega}(S) = S',</math> | ||
| + | <math>QH \cdot QO = QP^2 \implies I_{\Omega}(H) = O.</math> | ||
| + | <math>HS \perp DD' \implies S'O \perp BC \implies BS' = CS' \implies \angle OCS' = \angle OBS'.</math> | ||
| + | |||
| + | <math>\angle QSB = \angle QCS' = \angle OCS' = \angle OBS' = \angle CSS'.</math> | ||
| + | |||
| + | <math>\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.</math> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 15:38, 11 October 2022
Contents
[hide]Problem
Let ![]() be an acute triangle, and let
be an acute triangle, and let ![]() and
and ![]() denote its
denote its ![]() -excenter,
-excenter, ![]() -excenter, and circumcenter, respectively. Points
-excenter, and circumcenter, respectively. Points ![]() and
and ![]() are selected on
are selected on ![]() such that
such that ![]() and
and ![]() Similarly, points
Similarly, points ![]() and
and ![]() are selected on
are selected on ![]() such that
such that ![]() and
and ![]()
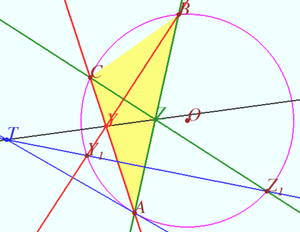
Lines ![]() and
and ![]() meet at
meet at ![]() Prove that
Prove that ![]() and
and ![]() are perpendicular.
are perpendicular.
Solution
This problem can be proved in the following two steps.
1. Let ![]() be the
be the ![]() -excenter, then
-excenter, then ![]() and
and ![]() are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for
are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for ![]()
2. Show that ![]() which implies
which implies ![]() This can be proved by multiple applications of the Pythagorean Thm.
This can be proved by multiple applications of the Pythagorean Thm.
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()
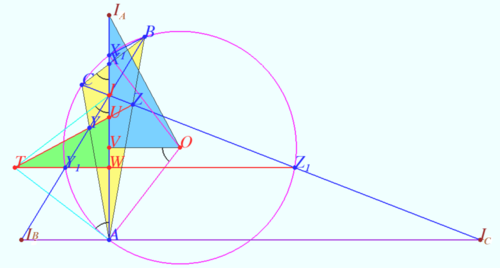
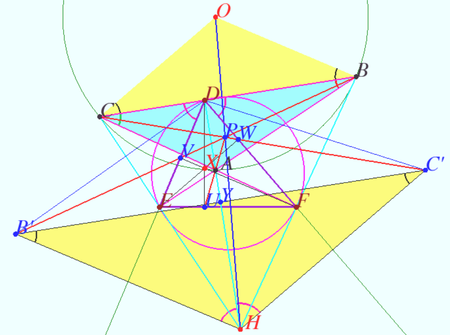
Solution 2
We find point ![]() on line
on line ![]() we prove that
we prove that ![]() and state that
and state that ![]() is the point
is the point ![]() from ENCYCLOPEDIA OF TRIANGLE, therefore
from ENCYCLOPEDIA OF TRIANGLE, therefore ![]()
Let ![]() be circumcircle of
be circumcircle of ![]() centered at
centered at ![]() Let
Let ![]() and
and ![]() be crosspoints of
be crosspoints of ![]() and
and ![]() and
and ![]() respectively.
Let
respectively.
Let ![]() be crosspoint of
be crosspoint of ![]() and
and ![]() In accordance the Pascal theorem for pentagon
In accordance the Pascal theorem for pentagon ![]()
![]() is tangent to
is tangent to ![]() at
at ![]()
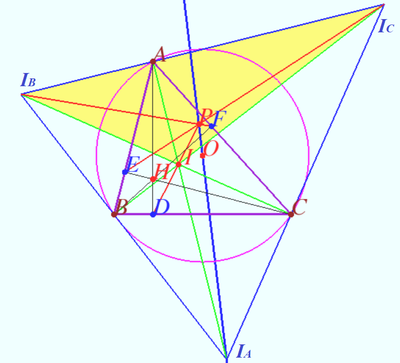
Let ![]() be
be ![]() and
and ![]() -excenters of
-excenters of ![]() Denote
Denote ![]()
![]()
![]()
![]() is the foot ot perpendicular from
is the foot ot perpendicular from ![]() to
to ![]()
![]() is ortocenter of
is ortocenter of ![]() and incenter of
and incenter of ![]()
![]() is the Nine–point circle of
is the Nine–point circle of ![]()
![]() is the midpoint of
is the midpoint of ![]() is the midpoint of
is the midpoint of ![]() in accordance with property of Nine–point circle
in accordance with property of Nine–point circle ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() In
In ![]() segment
segment ![]() cross segment
cross segment ![]() where
where ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Let ![]() be the base triangle with orthocenter
be the base triangle with orthocenter ![]() center of Nine-points circle
center of Nine-points circle ![]() be the Euler line of
be the Euler line of ![]()
![]() is orthic triangle of
is orthic triangle of ![]()
![]() is orthic-of-orthic triangle.
is orthic-of-orthic triangle.
![]() is perspector of base triangle and orthic-of-orthic triangle.
is perspector of base triangle and orthic-of-orthic triangle.
Therefore ![]() is point
is point ![]() of ENCYCLOPEDIA OF TRIANGLE CENTERS which lies on Euler line of the base triangle.
of ENCYCLOPEDIA OF TRIANGLE CENTERS which lies on Euler line of the base triangle.
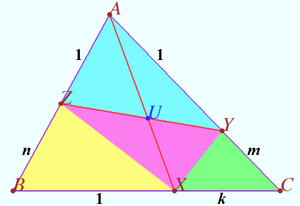
Claim ![]() Proof
Proof
![]()
![]()
![]()
![]()
![]()
Kimberling point X(24)
![]() Perspector of Triangle
Perspector of Triangle ![]() and Orthic Triangle of the Orthic Triangle.
Denote
and Orthic Triangle of the Orthic Triangle.
Denote ![]() obtuse or acute
obtuse or acute ![]() Let
Let ![]() be the base triangle,
be the base triangle, ![]() be Orthic triangle of
be Orthic triangle of ![]() be Orthic Triangle of the Orthic Triangle of
be Orthic Triangle of the Orthic Triangle of ![]() . Let
. Let ![]() and
and ![]() be the circumcenter and orthocenter of
be the circumcenter and orthocenter of ![]()
Then ![]() and
and ![]() are homothetic, the point
are homothetic, the point ![]() center of this homothety lies on Euler line
center of this homothety lies on Euler line ![]() of
of ![]()
The ratio of the homothety is ![]()
Proof
WLOG, we use case ![]() Let
Let ![]() be reflection
be reflection ![]() in
in ![]()
In accordance with Claim, ![]() and
and ![]() are collinear.
are collinear.
Similarly, ![]() and
and ![]() were
were ![]() is reflection
is reflection ![]() in
in ![]() are collinear.
are collinear.
Denote ![]()
![]()
![]()
![]()
![]() and
and ![]() are concurrent at point
are concurrent at point ![]()
In accordance with Claim, ![]() points
points ![]() and
and ![]() are isogonal conjugate with respect
are isogonal conjugate with respect ![]()
![]()
![]()
![]()
Claim
Let ![]() be an acute triangle, and let
be an acute triangle, and let ![]() and
and ![]() denote its altitudes. Lines
denote its altitudes. Lines ![]() and
and ![]() meet at
meet at ![]() Prove that
Prove that ![]()
Proof
Let ![]() be the circle
be the circle ![]() centered at
centered at ![]() is midpoint
is midpoint ![]()
Let ![]() meet
meet ![]() at
at ![]() Let
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
Let ![]() be the circle with diameter
be the circle with diameter ![]()
We know that ![]()
![]()
Let ![]() be inversion with respect
be inversion with respect ![]()
Denote ![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
See also
| 2016 USAMO (Problems • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||