Difference between revisions of "2015 AIME I Problems/Problem 4"
m (→Solution 3) |
(→Solution 2) |
||
| Line 62: | Line 62: | ||
The other way is to use the Mean Geometry Theorem. Note that <math>\triangle BCE</math> and <math>\triangle BDA</math> are similar and have the same orientation. Note that <math>B</math> is the weighted average of <math>B</math> and <math>B</math>, <math>M</math> is the weighted average of <math>E</math> and <math>A</math>, and <math>N</math> is the weighted average of <math>C</math> and <math>D</math>. The weights are the same for all three averages. (The weights are actually just <math>\frac{1}{2}</math> and <math>\frac{1}{2}</math>, so these are also unweighted averages.) Thus, by the Mean Geometry Theorem, <math>\triangle BMN</math> is similar to both <math>\triangle BAD</math> and <math>\triangle BEC</math>, which means that <math>\triangle BMN</math> is equilateral. | The other way is to use the Mean Geometry Theorem. Note that <math>\triangle BCE</math> and <math>\triangle BDA</math> are similar and have the same orientation. Note that <math>B</math> is the weighted average of <math>B</math> and <math>B</math>, <math>M</math> is the weighted average of <math>E</math> and <math>A</math>, and <math>N</math> is the weighted average of <math>C</math> and <math>D</math>. The weights are the same for all three averages. (The weights are actually just <math>\frac{1}{2}</math> and <math>\frac{1}{2}</math>, so these are also unweighted averages.) Thus, by the Mean Geometry Theorem, <math>\triangle BMN</math> is similar to both <math>\triangle BAD</math> and <math>\triangle BEC</math>, which means that <math>\triangle BMN</math> is equilateral. | ||
| + | |||
| + | |||
| + | *Note: A much easier way to go about finding <math>BM</math> without having to use Stewart's Theorem is to simply drop the altitudes from M and E to AC, thus hitting AC at points X and Y. Then clearly AEY and AMX are similar with ratio 2. But we know that <math>AY = 18 \implies AX = 9 \implies BX = 16-9 = 7</math>. Additionally, <math>MX = \frac{1}{2} (2\sqrt{3}) = \sqrt{3}</math> from similar triangles meaning we can now just do pythagorean theorem on right triangle <math>MXB</math> to get <math>MB = \sqrt{52}</math> - SuperJJ | ||
==Solution 3== | ==Solution 3== | ||
Revision as of 15:57, 23 November 2022
Contents
[hide]Problem
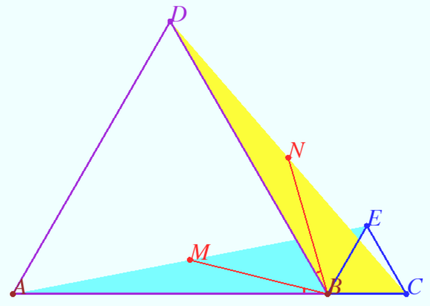
Point ![]() lies on line segment
lies on line segment ![]() with
with ![]() and
and ![]() . Points
. Points ![]() and
and ![]() lie on the same side of line
lie on the same side of line ![]() forming equilateral triangles
forming equilateral triangles ![]() and
and ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() , and
, and ![]() be the midpoint of
be the midpoint of ![]() . The area of
. The area of ![]() is
is ![]() . Find
. Find ![]() .
.
Diagram
![[asy] pair A = (0, 0), B = (16, 0), C = (20, 0), D = (8, 8*sqrt(3)), EE = (18, 2*sqrt(3)), M = (9, sqrt(3)), NN = (14, 4*sqrt(3)); draw(A--B--D--cycle); draw(B--C--EE--cycle); draw(A--EE); draw(C--D); draw(B--M--NN--cycle); dot(A); dot(B); dot(C); dot(D); dot(EE); dot(M); dot(NN); label("A", A, SW); label("B", B, S); label("C", C, SE); label("D", D, N); label("E", EE, N); label("M", M, NW); label("N", NN, NE); [/asy]](http://latex.artofproblemsolving.com/2/2/2/222ea4031f51c1923ced2de0bdf1e1f8e161a1cc.png)
Diagram by RedFireTruck (talk) 18:52, 15 February 2021 (EST)
Solution 1
Let ![]() be the origin, so
be the origin, so ![]() and
and ![]() Using equilateral triangle properties tells us that
Using equilateral triangle properties tells us that ![]() and
and ![]() as well. Therefore,
as well. Therefore, ![]() and
and ![]() Applying the Shoelace Theorem to triangle
Applying the Shoelace Theorem to triangle ![]() gives
gives
![]()
so ![]()
Solution 2
Note that ![]() and
and ![]() . Also,
. Also, ![]() . Thus,
. Thus, ![]() by SAS.
by SAS.
From this, it is clear that a ![]() rotation about
rotation about ![]() will map
will map ![]() to
to ![]() .
This rotation also maps
.
This rotation also maps ![]() to
to ![]() . Thus,
. Thus, ![]() and
and ![]() . Thus,
. Thus, ![]() is equilateral.
is equilateral.
Using the Law of Cosines on ![]() ,
,
![]()
![]() Thus,
Thus, ![]() .
.
Using Stewart's Theorem on ![]() ,
,
![]()
![]()
Calculating the area of ![]() ,
,
![]()
![]() Thus,
Thus, ![]() , so
, so ![]() . Our final answer is
. Our final answer is ![]() .
.
Admittedly, this is much more tedious than the coordinate solutions.
I also noticed that there are two more ways of showing that ![]() is equilateral:
is equilateral:
One way is to show that ![]() ,
, ![]() , and
, and ![]() are related by a spiral similarity centered at
are related by a spiral similarity centered at ![]() .
.
The other way is to use the Mean Geometry Theorem. Note that ![]() and
and ![]() are similar and have the same orientation. Note that
are similar and have the same orientation. Note that ![]() is the weighted average of
is the weighted average of ![]() and
and ![]() ,
, ![]() is the weighted average of
is the weighted average of ![]() and
and ![]() , and
, and ![]() is the weighted average of
is the weighted average of ![]() and
and ![]() . The weights are the same for all three averages. (The weights are actually just
. The weights are the same for all three averages. (The weights are actually just ![]() and
and ![]() , so these are also unweighted averages.) Thus, by the Mean Geometry Theorem,
, so these are also unweighted averages.) Thus, by the Mean Geometry Theorem, ![]() is similar to both
is similar to both ![]() and
and ![]() , which means that
, which means that ![]() is equilateral.
is equilateral.
- Note: A much easier way to go about finding
 without having to use Stewart's Theorem is to simply drop the altitudes from M and E to AC, thus hitting AC at points X and Y. Then clearly AEY and AMX are similar with ratio 2. But we know that
without having to use Stewart's Theorem is to simply drop the altitudes from M and E to AC, thus hitting AC at points X and Y. Then clearly AEY and AMX are similar with ratio 2. But we know that  . Additionally,
. Additionally,  from similar triangles meaning we can now just do pythagorean theorem on right triangle
from similar triangles meaning we can now just do pythagorean theorem on right triangle  to get
to get  - SuperJJ
- SuperJJ
Solution 3
![]()
Medians are equal, so ![]()
![]()
![]() is equilateral triangle.
is equilateral triangle.
The height of ![]() is
is ![]() distance from
distance from ![]() to midpoint
to midpoint ![]() is
is ![]()
![]() is the median of
is the median of ![]()
![]()
The area of ![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2015 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()