Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2001 AIME I Problems/Problem 13"
m (Did not include answer)
 
(25 intermediate revisions by 11 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
 +
In a certain [[circle]], the [[chord]] of a <math>d</math>-degree arc is <math>22</math> centimeters long, and the chord of a <math>2d</math>-degree arc is <math>20</math> centimeters longer than the chord of a <math>3d</math>-degree arc, where <math>d < 120.</math>  The length of the chord of a <math>3d</math>-degree arc is <math>- m + \sqrt {n}</math> centimeters, where <math>m</math> and <math>n</math> are positive integers.  Find <math>m + n.</math>
  
 
== Solution ==
 
== Solution ==
 +
 +
=== Solution 1 ===
 +
<center>[[File:2001AIME13.png]]</center>
 +
 +
Note that a cyclic quadrilateral in the form of an isosceles trapezoid can be formed from three chords of three <math>d</math>-degree arcs and one chord of one <math>3d</math>-degree arc. The diagonals of this trapezoid turn out to be two chords of two <math>2d</math>-degree arcs. Let <math>AB</math>, <math>AC</math>, and <math>BD</math> be the chords of the <math>d</math>-degree arcs, and let <math>CD</math> be the chord of the <math>3d</math>-degree arc. Also let <math>x</math> be equal to the chord length of the <math>3d</math>-degree arc. Hence, the length of the chords, <math>AD</math> and <math>BC</math>, of the <math>2d</math>-degree arcs can be represented as <math>x + 20</math>, as given in the problem.
 +
 +
Using Ptolemy's theorem,
 +
 +
<cmath>AB(CD) + AC(BD) = AD(BC)</cmath>
 +
<cmath>22x + 22(22)  = (x + 20)^2</cmath>
 +
<cmath>22x + 484 = x^2 + 40x + 400</cmath>
 +
<cmath>0 = x^2 + 18x - 84</cmath>
 +
 +
We can then apply the quadratic formula to find the positive root to this equation since polygons obviously cannot have sides of negative length.
 +
<cmath>x = \frac{-18 + \sqrt{18^2 + 4(84)}}{2}</cmath>
 +
<cmath>x = \frac{-18 + \sqrt{660}}{2}</cmath>
 +
 +
<math>x</math> simplifies to <math>\frac{-18 + 2\sqrt{165}}{2},</math> which equals <math>-9 + \sqrt{165}.</math> Thus, the answer is <math>9 + 165 = \boxed{174}</math>.
 +
 +
=== Solution 2 ===
 +
 +
Let <math>z=\frac{d}{2},</math> and <math>R</math> be the circumradius. From the given information, <cmath>2R\sin z=22</cmath> <cmath>2R(\sin 2z-\sin 3z)=20</cmath> Dividing the latter by the former, <cmath>\frac{2\sin z\cos z-(3\cos^2z\sin z-\sin^3 z)}{\sin z}=2\cos z-(3\cos^2z-\sin^2z)=1+2\cos z-4\cos^2z=\frac{10}{11}</cmath> <cmath>4\cos^2z-2\cos z-\frac{1}{11}=0 (1)</cmath> We want to find <cmath>\frac{22\sin (3z)}{\sin z}=22(3-4\sin^2z)=22(4\cos^2z-1).</cmath> From <math>(1),</math> this is equivalent to <math>44\cos z-20.</math> Using the quadratic formula, we find that the desired length is equal to <math>\sqrt{165}-9,</math> so our answer is <math>\boxed{174}</math>
 +
 +
===Solution 3===
 +
 +
Let <math>z=\frac{d}{2}</math>, <math>R</math> be the circumradius, and <math>a</math> be the length of 3d degree chord. Using the extended sine law, we obtain:
 +
<cmath>22=2R\sin(z)</cmath>
 +
<cmath>20+a=2R\sin(2z)</cmath>
 +
<cmath>a=2R\sin(3z)</cmath>
 +
Dividing the second from the first we get <math>\cos(z)=\frac{20+a}{44}</math>
 +
By the triple angle formula we can manipulate the third equation as follows: <math>a=2R\times \sin(3z)=\frac{22}{\sin(z)} \times (3\sin(z)-4\sin^3(z)) = 22(3-4\sin^2(z))=22(4\cos^2(z)-1)=\frac{(20+a)^2}{22}-22</math>
 +
Solving the quadratic equation gives the answer to be <math>\boxed{174}</math>.
  
 
== See also ==
 
== See also ==
−
* [[2001 AIME I Problems/Problem 12 | Previous Problem]]
+
{{AIME box|year=2001|n=I|num-b=12|num-a=14}}
−
 
 
−
* [[2001 AIME I Problems/Problem 14 | Next Problem]]
 
  
−
* [[2001 AIME I Problems]]
+
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 18:25, 27 November 2022

Problem

In a certain circle, the chord of a $d$-degree arc is $22$ centimeters long, and the chord of a $2d$-degree arc is $20$ centimeters longer than the chord of a $3d$-degree arc, where $d < 120.$ The length of the chord of a $3d$-degree arc is $- m + \sqrt {n}$ centimeters, where $m$ and $n$ are positive integers. Find $m + n.$

Solution

Solution 1

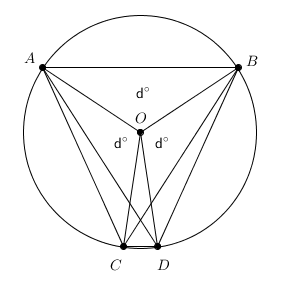
2001AIME13.png

Note that a cyclic quadrilateral in the form of an isosceles trapezoid can be formed from three chords of three $d$-degree arcs and one chord of one $3d$-degree arc. The diagonals of this trapezoid turn out to be two chords of two $2d$-degree arcs. Let $AB$, $AC$, and $BD$ be the chords of the $d$-degree arcs, and let $CD$ be the chord of the $3d$-degree arc. Also let $x$ be equal to the chord length of the $3d$-degree arc. Hence, the length of the chords, $AD$ and $BC$, of the $2d$-degree arcs can be represented as $x + 20$, as given in the problem.

Using Ptolemy's theorem,

\[AB(CD) + AC(BD) = AD(BC)\] \[22x + 22(22) = (x + 20)^2\] \[22x + 484 = x^2 + 40x + 400\] \[0 = x^2 + 18x - 84\]

We can then apply the quadratic formula to find the positive root to this equation since polygons obviously cannot have sides of negative length. \[x = \frac{-18 + \sqrt{18^2 + 4(84)}}{2}\] \[x = \frac{-18 + \sqrt{660}}{2}\]

$x$ simplifies to $\frac{-18 + 2\sqrt{165}}{2},$ which equals $-9 + \sqrt{165}.$ Thus, the answer is $9 + 165 = \boxed{174}$.

Solution 2

Let $z=\frac{d}{2},$ and $R$ be the circumradius. From the given information, \[2R\sin z=22\] \[2R(\sin 2z-\sin 3z)=20\] Dividing the latter by the former, \[\frac{2\sin z\cos z-(3\cos^2z\sin z-\sin^3 z)}{\sin z}=2\cos z-(3\cos^2z-\sin^2z)=1+2\cos z-4\cos^2z=\frac{10}{11}\] \[4\cos^2z-2\cos z-\frac{1}{11}=0 (1)\] We want to find \[\frac{22\sin (3z)}{\sin z}=22(3-4\sin^2z)=22(4\cos^2z-1).\] From $(1),$ this is equivalent to $44\cos z-20.$ Using the quadratic formula, we find that the desired length is equal to $\sqrt{165}-9,$ so our answer is $\boxed{174}$

Solution 3

Let $z=\frac{d}{2}$, $R$ be the circumradius, and $a$ be the length of 3d degree chord. Using the extended sine law, we obtain: \[22=2R\sin(z)\] \[20+a=2R\sin(2z)\] \[a=2R\sin(3z)\] Dividing the second from the first we get $\cos(z)=\frac{20+a}{44}$ By the triple angle formula we can manipulate the third equation as follows: $a=2R\times \sin(3z)=\frac{22}{\sin(z)} \times (3\sin(z)-4\sin^3(z)) = 22(3-4\sin^2(z))=22(4\cos^2(z)-1)=\frac{(20+a)^2}{22}-22$ Solving the quadratic equation gives the answer to be $\boxed{174}$.

See also

2001 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 12 		Followed by
Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2001_AIME_I_Problems/Problem_13&oldid=183176"