Difference between revisions of "2006 Cyprus MO/Lyceum/Problem 11"
m (→Solution: \left(right)) |
|||
| Line 25: | Line 25: | ||
<math>B=(0,4)</math> | <math>B=(0,4)</math> | ||
| − | <math>\Gamma =(\frac{8}{3},\frac{4}{3})</math> | + | <math>\Gamma =\left(\frac{8}{3},\frac{4}{3}\right)</math> |
We find the area of triangles: | We find the area of triangles: | ||
Revision as of 11:40, 21 October 2007
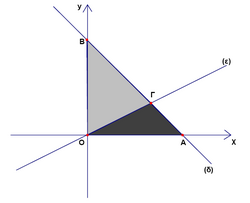
Problem
The lines ![]() and
and ![]() intersect at the point
intersect at the point ![]() . If the line
. If the line ![]() intersects the axes
intersects the axes ![]() and
and ![]() to the points
to the points ![]() and
and ![]() respectively, then the ratio of the area of the triangle
respectively, then the ratio of the area of the triangle ![]() to the area of the triangle
to the area of the triangle ![]() equals
equals
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Solution
We find some coordinates:
![]()
![]()
![]()
![]()
We find the area of triangles:
![]()
![]()
![]()
![]()
See also
| 2006 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||