Difference between revisions of "2020 AIME II Problems/Problem 15"
m (→Solution) |
m (→Solution 1) |
||
| Line 3: | Line 3: | ||
==Solution 1== | ==Solution 1== | ||
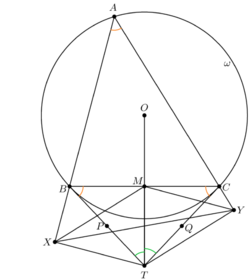
| − | + | Let <math>O</math> be the circumcenter of <math>\triangle ABC</math>; say <math>OT</math> intersects <math>BC</math> at <math>M</math>; draw segments <math>XM</math>, and <math>YM</math>. We have <math>MT=3\sqrt{15}</math>. | |
| + | |||
| + | [[File:Fanyuchen.png|250px|right]] | ||
| + | |||
| + | Since <math>\angle A=\angle CBT=\angle BCT</math>, we have <math>\cos A=\tfrac{11}{16}</math>. Notice that <math>AXTY</math> is cyclic, so <math>\angle XTY=180^{\circ}-A</math>, so <math>\cos XTY=-\cos A</math>, and the cosine law in <math>\triangle TXY</math> gives <cmath>1143-2XY^2=-\frac{11}{8}\cdot XT\cdot YT.</cmath> | ||
| + | |||
| + | Since <math>\triangle BMT \cong \triangle CMT</math>, we have <math>TM\perp BC</math>, and therefore quadrilaterals <math>BXTM</math> and <math>CYTM</math> are cyclic. Let <math>P</math> (resp. <math>Q</math>) be the midpoint of <math>BT</math> (resp. <math>CT</math>). So <math>P</math> (resp. <math>Q</math>) is the center of <math>(BXTM)</math> (resp. <math>CYTM</math>). Then <math>\theta=\angle ABC=\angle MTX</math> and <math>\phi=\angle ACB=\angle YTM</math>. So <math>\angle XPM=2\theta</math>, so<cmath>\frac{\frac{XM}{2}}{XP}=\sin \theta,</cmath>which yields <math>XM=2XP\sin \theta=BT(=CT)\sin \theta=TY</math>. Similarly we have <math>YM=XT</math>. | ||
| + | |||
| + | Ptolemy's theorem in <math>BXTM</math> gives <cmath>16TY=11TX+3\sqrt{15}BX,</cmath> while Pythagoras' theorem gives <math>BX^2+XT^2=16^2</math>. Similarly, Ptolemy's theorem in <math>YTMC</math> gives<cmath>16TX=11TY+3\sqrt{15}CY</cmath> while Pythagoras' theorem in <math>\triangle CYT</math> gives <math>CY^2+YT^2=16^2</math>. Solve this for <math>XT</math> and <math>TY</math> and substitute into the equation about <math>\cos XTY</math> to obtain the result <math>XY^2=\boxed{717}</math>. | ||
(Notice that <math>MXTY</math> is a parallelogram, which is an important theorem in Olympiad, and there are some other ways of computation under this observation.) | (Notice that <math>MXTY</math> is a parallelogram, which is an important theorem in Olympiad, and there are some other ways of computation under this observation.) | ||
Revision as of 16:55, 4 January 2023
Contents
[hide]Problem
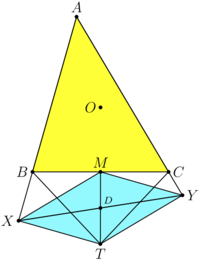
Let ![]() be an acute scalene triangle with circumcircle
be an acute scalene triangle with circumcircle ![]() . The tangents to
. The tangents to ![]() at
at ![]() and
and ![]() intersect at
intersect at ![]() . Let
. Let ![]() and
and ![]() be the projections of
be the projections of ![]() onto lines
onto lines ![]() and
and ![]() , respectively. Suppose
, respectively. Suppose ![]() ,
, ![]() , and
, and ![]() . Find
. Find ![]() .
.
Solution 1
Let ![]() be the circumcenter of
be the circumcenter of ![]() ; say
; say ![]() intersects
intersects ![]() at
at ![]() ; draw segments
; draw segments ![]() , and
, and ![]() . We have
. We have ![]() .
.
Since ![]() , we have
, we have ![]() . Notice that
. Notice that ![]() is cyclic, so
is cyclic, so ![]() , so
, so ![]() , and the cosine law in
, and the cosine law in ![]() gives
gives ![]()
Since ![]() , we have
, we have ![]() , and therefore quadrilaterals
, and therefore quadrilaterals ![]() and
and ![]() are cyclic. Let
are cyclic. Let ![]() (resp.
(resp. ![]() ) be the midpoint of
) be the midpoint of ![]() (resp.
(resp. ![]() ). So
). So ![]() (resp.
(resp. ![]() ) is the center of
) is the center of ![]() (resp.
(resp. ![]() ). Then
). Then ![]() and
and ![]() . So
. So ![]() , so
, so![]() which yields
which yields ![]() . Similarly we have
. Similarly we have ![]() .
.
Ptolemy's theorem in ![]() gives
gives ![]() while Pythagoras' theorem gives
while Pythagoras' theorem gives ![]() . Similarly, Ptolemy's theorem in
. Similarly, Ptolemy's theorem in ![]() gives
gives![]() while Pythagoras' theorem in
while Pythagoras' theorem in ![]() gives
gives ![]() . Solve this for
. Solve this for ![]() and
and ![]() and substitute into the equation about
and substitute into the equation about ![]() to obtain the result
to obtain the result ![]() .
.
(Notice that ![]() is a parallelogram, which is an important theorem in Olympiad, and there are some other ways of computation under this observation.)
is a parallelogram, which is an important theorem in Olympiad, and there are some other ways of computation under this observation.)
-Fanyuchen20020715
Solution 2 (Official MAA)
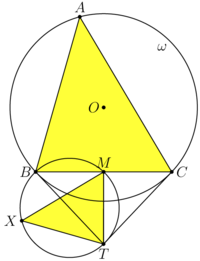
Let ![]() denote the midpoint of
denote the midpoint of ![]() . The critical claim is that
. The critical claim is that ![]() is the orthocenter of
is the orthocenter of ![]() , which has the circle with diameter
, which has the circle with diameter ![]() as its circumcircle. To see this, note that because
as its circumcircle. To see this, note that because ![]() , the quadrilateral
, the quadrilateral ![]() is cyclic, it follows that
is cyclic, it follows that
![]() implying that
implying that ![]() . Similarly,
. Similarly, ![]() . In particular,
. In particular, ![]() is a parallelogram.
is a parallelogram.
![[asy] defaultpen(fontsize(8pt)); unitsize(0.8cm); pair A = (0,0); pair B = (-1.26,-4.43); pair C = (-1.26+3.89, -4.43); pair M = (B+C)/2; pair O = circumcenter(A,B,C); pair T = (0.68, -6.49); pair X = foot(T,A,B); pair Y = foot(T,A,C); path omega = circumcircle(A,B,C); real rad = circumradius(A,B,C); filldraw(A--B--C--cycle, 0.2*royalblue+white); label("$\omega$", O + rad*dir(45), SW); //filldraw(T--Y--M--X--cycle, rgb(150, 247, 254)); filldraw(T--Y--M--X--cycle, 0.2*heavygreen+white); draw(M--T); draw(X--Y); draw(B--T--C); draw(A--X--Y--cycle); draw(omega); dot("$X$", X, W); dot("$Y$", Y, E); dot("$O$", O, W); dot("$T$", T, S); dot("$A$", A, N); dot("$B$", B, W); dot("$C$", C, E); dot("$M$", M, N); [/asy]](http://latex.artofproblemsolving.com/b/3/7/b37485262f643e08b4b17f0839d8e651976343d9.png) Hence, by the Parallelogram Law,
Hence, by the Parallelogram Law,
![]() But
But ![]() . Therefore
. Therefore ![]()
Solution 3 (Law of Cosines)
Let ![]() be the orthocenter of
be the orthocenter of ![]() .
.
Lemma 1: ![]() is the midpoint of
is the midpoint of ![]() .
.
Proof: Let ![]() be the midpoint of
be the midpoint of ![]() , and observe that
, and observe that ![]() and
and ![]() are cyclical. Define
are cyclical. Define ![]() and
and ![]() , then note that:
, then note that:
![]() That implies that
That implies that ![]() ,
, ![]() , and
, and ![]() . Thus
. Thus ![]() and
and ![]() ;
; ![]() is indeed the same as
is indeed the same as ![]() , and we have proved lemma 1.
, and we have proved lemma 1.
Since ![]() is cyclical,
is cyclical, ![]() and this implies that
and this implies that ![]() is a paralelogram.
By the Law of Cosines:
is a paralelogram.
By the Law of Cosines:
![]()
![]()
![]()
![]() We add all these equations to get:
We add all these equations to get:
![]() We have that
We have that ![]() and
and ![]() using our midpoints. Note that
using our midpoints. Note that ![]() , so by the Pythagorean Theorem, it follows that
, so by the Pythagorean Theorem, it follows that ![]() . We were also given that
. We were also given that ![]() , which we multiply by
, which we multiply by ![]() to use equation
to use equation ![]() .
. ![]() Since
Since ![]() , we have
, we have
![]()
![]() Therefore,
Therefore, ![]() . ~ MathLuis
. ~ MathLuis
Solution 4 (Similarity and median)
Using the Claim (below) we get ![]()
Corresponding sides of similar ![]() is
is ![]() so
so
![]() – parallelogram.
– parallelogram.
![]() The formula for median
The formula for median ![]() of triangle
of triangle ![]() is
is
![]()
![]()
![]()
Claim
Let ![]() be an acute scalene triangle with circumcircle
be an acute scalene triangle with circumcircle ![]() . The tangents to
. The tangents to ![]() at
at ![]() and
and ![]() intersect at
intersect at ![]() . Let
. Let ![]() be the projections of
be the projections of ![]() onto line
onto line ![]() . Let M be midpoint BC. Then triangle ABC is similar to triangle XTM.
. Let M be midpoint BC. Then triangle ABC is similar to triangle XTM.
Proof
![]() the quadrilateral
the quadrilateral ![]() is cyclic.
is cyclic.
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2020 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()