Difference between revisions of "2023 AIME I Problems/Problem 12"
m (→Solution 5) |
Fuzimiao2013 (talk | contribs) m (→Solution) |
||
| Line 2: | Line 2: | ||
Let <math>\triangle ABC</math> be an equilateral triangle with side length <math>55.</math> Points <math>D,</math> <math>E,</math> and <math>F</math> lie on <math>\overline{BC},</math> <math>\overline{CA},</math> and <math>\overline{AB},</math> respectively, with <math>BD = 7,</math> <math>CE=30,</math> and <math>AF=40.</math> Point <math>P</math> inside <math>\triangle ABC</math> has the property that <cmath>\angle AEP = \angle BFP = \angle CDP.</cmath> Find <math>\tan^2(\angle AEP).</math> | Let <math>\triangle ABC</math> be an equilateral triangle with side length <math>55.</math> Points <math>D,</math> <math>E,</math> and <math>F</math> lie on <math>\overline{BC},</math> <math>\overline{CA},</math> and <math>\overline{AB},</math> respectively, with <math>BD = 7,</math> <math>CE=30,</math> and <math>AF=40.</math> Point <math>P</math> inside <math>\triangle ABC</math> has the property that <cmath>\angle AEP = \angle BFP = \angle CDP.</cmath> Find <math>\tan^2(\angle AEP).</math> | ||
| − | ==Solution== | + | ==Solution (Coord bash)== |
By Miquel's theorem, <math>P=(AEF)\cap(BFD)\cap(CDE)</math> (intersection of circles). The law of cosines can be used to compute <math>DE=42</math>, <math>EF=35</math>, and <math>FD=13</math>. Toss the points on the coordinate plane; let <math>B=(-7, 0)</math>, <math>D=(0, 0)</math>, and <math>C=(48, 0)</math>, where we will find <math>\tan^{2}\left(\measuredangle CDP\right)</math> with <math>P=(BFD)\cap(CDE)</math>. | By Miquel's theorem, <math>P=(AEF)\cap(BFD)\cap(CDE)</math> (intersection of circles). The law of cosines can be used to compute <math>DE=42</math>, <math>EF=35</math>, and <math>FD=13</math>. Toss the points on the coordinate plane; let <math>B=(-7, 0)</math>, <math>D=(0, 0)</math>, and <math>C=(48, 0)</math>, where we will find <math>\tan^{2}\left(\measuredangle CDP\right)</math> with <math>P=(BFD)\cap(CDE)</math>. | ||
Revision as of 01:28, 14 February 2023
Contents
Problem
Let ![]() be an equilateral triangle with side length
be an equilateral triangle with side length ![]() Points
Points ![]()
![]() and
and ![]() lie on
lie on ![]()
![]() and
and ![]() respectively, with
respectively, with ![]()
![]() and
and ![]() Point
Point ![]() inside
inside ![]() has the property that
has the property that ![]() Find
Find ![]()
Solution (Coord bash)
By Miquel's theorem, ![]() (intersection of circles). The law of cosines can be used to compute
(intersection of circles). The law of cosines can be used to compute ![]() ,
, ![]() , and
, and ![]() . Toss the points on the coordinate plane; let
. Toss the points on the coordinate plane; let ![]() ,
, ![]() , and
, and ![]() , where we will find
, where we will find ![]() with
with ![]() .
.
By the extended law of sines, the radius of circle ![]() is
is ![]() . Its center lies on the line
. Its center lies on the line ![]() , and the origin is a point on it, so
, and the origin is a point on it, so ![]() .
.
The radius of circle ![]() is
is ![]() . The origin is also a point on it, and its center is on the line
. The origin is also a point on it, and its center is on the line ![]() , so
, so ![]() .
.
The equations of the two circles are  These equations simplify to
These equations simplify to  Subtracting these two equations gives that both their points of intersection,
Subtracting these two equations gives that both their points of intersection, ![]() and
and ![]() , lie on the line
, lie on the line ![]() . Hence,
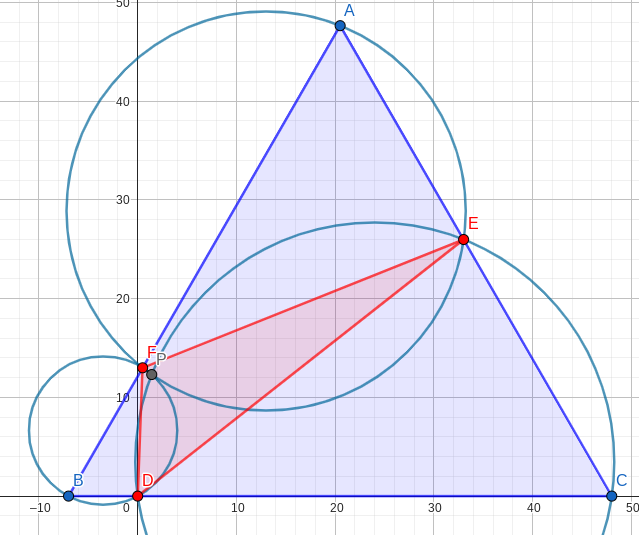
. Hence,  . To scale, the configuration looks like the figure below.
. To scale, the configuration looks like the figure below.
Solution 2
Denote ![]() .
.
In ![]() , we have
, we have ![]() .
Thus,
.
Thus,
![]()
Taking the real and imaginary parts, we get
![]()
In ![]() , analogous to the analysis of
, analogous to the analysis of ![]() above, we get
above, we get
![]()
Taking ![]() , we get
, we get
![]()
Taking ![]() , we get
, we get
![]()
Taking ![]() , we get
, we get
![]()
Therefore,

Therefore, ![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 3 (no trig)
Drop the perpendiculars from ![]() to
to ![]() ,
, ![]() ,
, ![]() , and call them
, and call them ![]() and
and ![]() respectively. This gives us three similar right triangles
respectively. This gives us three similar right triangles ![]() ,
, ![]() , and
, and ![]()
The sum of the perpendiculars to a point ![]() within an equilateral triangle is always constant, so we have that
within an equilateral triangle is always constant, so we have that ![]()
The sum of the lengths of the alternating segments split by the perpendiculars from a point ![]() within an equilateral triangle is always equal to half the perimeter, so
within an equilateral triangle is always equal to half the perimeter, so ![]() which means that
which means that ![]()
Finally, ![]()
Thus, ![]()
~anon
Solution 4 (LOC)
This solution is heavily inspired by AIME 1999 Problem 14 Solution 2 (a similar question)
Draw line segments from ![]() to points
to points ![]() ,
, ![]() , and
, and ![]() . And label the angle measure of
. And label the angle measure of ![]() ,
, ![]() , and
, and ![]() to be
to be ![]()
Using Law of Cosines (note that ![]() )
)

We can perform this operation: (1) - (2) + (3) - (4) + (5) - (6)
Leaving us with (after combining and simplifying)
![]()
Therefore, we want to solve for ![]()
Notice that ![]()
We can use Law of Cosines again to solve for the sides of ![]() , which have side lengths of
, which have side lengths of ![]() ,
, ![]() , and
, and ![]() , and area
, and area ![]() .
.
Label the lengths of ![]() ,
, ![]() , and
, and ![]() to be
to be ![]() ,
, ![]() , and
, and ![]() .
.
Therefore, using the ![]() area formula,
area formula,
![\begin{align*} [\triangle{DEF}] &= \frac{1}{2}*\sin{120°}*(xy+yz+zx) = 120\sqrt{3} \\ xy+yz+zx &= 2^5*3*5 \end{align*}](http://latex.artofproblemsolving.com/4/6/f/46f28677018afb89dba4c139089b55dd04d2db87.png)
In addition, we know that

By using Law of Cosines for ![]() ,
, ![]() , and
, and ![]() respectively
respectively
Because we want ![]() , which is
, which is ![]() , we see that
, we see that

So plugging the results back into the equation before, we get

Giving us
![]()
~Danielzh
Solution 5
By the law of cosines,
![]() Similarly we get
Similarly we get ![]() and
and ![]() .
. ![]() implies that
implies that ![]() ,
, ![]() , and
, and ![]() are three cyclic quadrilaterals. Using the law of sines in each,
are three cyclic quadrilaterals. Using the law of sines in each,
![]() So we can set
So we can set ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() . Applying Ptolemy theorem in the cyclic quadrilaterals,
. Applying Ptolemy theorem in the cyclic quadrilaterals,
![\[\begin{cases}AP\cdot FE=AF\cdot PE+AE\cdot PF,\\CP\cdot ED=CE\cdot PD+CD\cdot PE,\\BP\cdot DF=BD\cdot PF+BF\cdot PD.\end{cases} \implies \begin{cases} 1225k=40e+25f,\\1764k=30d+48e,\\169k=15d+7f, \end{cases}\]](http://latex.artofproblemsolving.com/2/9/7/297912a1434ac5ec975494ce5b2033976ff72466.png) We can solve out
We can solve out ![]() ,
, ![]() ,
, ![]() . By the law of cosines in
. By the law of cosines in ![]() ,
,  . The law of sines yield
. The law of sines yield ![]() .
Lastly,
.
Lastly, ![]() , then
, then ![]() . The answer is
. The answer is
![]()
See also
| 2023 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.