Difference between revisions of "2001 AIME II Problems/Problem 8"
Magnetoninja (talk | contribs) (→Solution 2 (Graphing)) |
Magnetoninja (talk | contribs) (→Solution 2 (Graphing)) |
||
| Line 26: | Line 26: | ||
First, we start by graphing the function when <math>1\leq{x}\leq3</math>, which consists of the lines <math>y=x-1</math> and <math>y=3-x</math> that intersect at <math>(2,1)</math>. Similarly, using <math>f(3x)=3f(x)</math>, we get a dilation of our initial figure by a factor of 3 for the next interval and so on. | First, we start by graphing the function when <math>1\leq{x}\leq3</math>, which consists of the lines <math>y=x-1</math> and <math>y=3-x</math> that intersect at <math>(2,1)</math>. Similarly, using <math>f(3x)=3f(x)</math>, we get a dilation of our initial figure by a factor of 3 for the next interval and so on. | ||
Observe that the intersection of two lines always has coordinates <math>(2y,y)</math> where <math>y=3^a</math> for some <math>a</math>. First, we compute <math>f(2001)</math>. The nearest intersection point is <math>(1458,729)</math> when <math>a=7</math>. Therefore, we can safely assume that <math>f(2001)</math> is somewhere on the line with a slope of <math>-1</math> that intersects at that nearest point. Using the fact that the slope of the line is <math>-1</math>, we compute <math>f(2001)=729-543=186</math>. However, we want the minimum value such that <math>f(x)=186</math> and we see that there is another intersection point on the left which has a <math>y>186</math>, namely <math>(486,243)</math>. Therefore, we want the point that lies on the line with slope <math>1</math> that intersects this point. Once again, since the slope of the line is <math>1</math>, we get <math>x=486-57=\boxed{429}</math>. | Observe that the intersection of two lines always has coordinates <math>(2y,y)</math> where <math>y=3^a</math> for some <math>a</math>. First, we compute <math>f(2001)</math>. The nearest intersection point is <math>(1458,729)</math> when <math>a=7</math>. Therefore, we can safely assume that <math>f(2001)</math> is somewhere on the line with a slope of <math>-1</math> that intersects at that nearest point. Using the fact that the slope of the line is <math>-1</math>, we compute <math>f(2001)=729-543=186</math>. However, we want the minimum value such that <math>f(x)=186</math> and we see that there is another intersection point on the left which has a <math>y>186</math>, namely <math>(486,243)</math>. Therefore, we want the point that lies on the line with slope <math>1</math> that intersects this point. Once again, since the slope of the line is <math>1</math>, we get <math>x=486-57=\boxed{429}</math>. | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Magnetoninja Magnetoninja] | ||
== See also == | == See also == | ||
Revision as of 22:41, 14 June 2023
Problem
A certain function 
has the properties that 
for all positive real values of 
, and that 
for 
. Find the smallest for which 
.
Solution
Iterating the condition , we find that 
for positive integers 
. We know the definition of 
from 
, so we would like to express 
. Indeed,
![\[f(2001) = 729\left[1 - \left| \frac{2001}{729} - 2\right|\right] = 186.\]](http://latex.artofproblemsolving.com/e/1/2/e129ad258113f974ab9e842efa3433c64a365217.png)
We now need the smallest such that 
. The range of 
, is 
. So when 
, we have 
. Multiplying by 
: 
, so the smallest value of is 
. Then,
![\[186 = {3^5}f\left(\frac{x}{3^5}\right).\]](http://latex.artofproblemsolving.com/0/6/f/06f2b37921ee653205a539b6c9e2ab0be7c9a924.png)
Because we forced 
, so
![\[186 = {3^5}f\left(\frac{x}{3^5}\right) = 243\left[1 - \left| \frac{x}{243} - 2\right|\right] \Longrightarrow x = \pm 57 + 2 \cdot 243.\]](http://latex.artofproblemsolving.com/9/1/c/91c437fd96b60bcc9002ced02a93d102b03ce54a.png)
We want the smaller value of 
.
An alternative approach is to consider the graph of , which iterates every power of 
, and resembles the section from dilated by a factor of at each iteration.
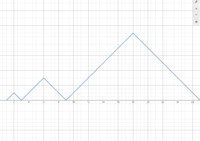
Solution 2 (Graphing)
First, we start by graphing the function when 
, which consists of the lines 
and 
that intersect at 
. Similarly, using 
, we get a dilation of our initial figure by a factor of 3 for the next interval and so on.
Observe that the intersection of two lines always has coordinates 
where 
for some 
. First, we compute 
. The nearest intersection point is 
when 
. Therefore, we can safely assume that is somewhere on the line with a slope of 
that intersects at that nearest point. Using the fact that the slope of the line is , we compute 
. However, we want the minimum value such that 
and we see that there is another intersection point on the left which has a 
, namely 
. Therefore, we want the point that lies on the line with slope 
that intersects this point. Once again, since the slope of the line is , we get 
.
See also
| 2001 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
