Difference between revisions of "1989 AIME Problems"
(→Problem 8) |
|||
| (18 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{AIME Problems|year=1989}} | ||
| + | |||
== Problem 1 == | == Problem 1 == | ||
| + | Compute <math>\sqrt{(31)(30)(29)(28)+1}</math>. | ||
[[1989 AIME Problems/Problem 1|Solution]] | [[1989 AIME Problems/Problem 1|Solution]] | ||
== Problem 2 == | == Problem 2 == | ||
| + | Ten points are marked on a circle. How many distinct convex polygons of three or more sides can be drawn using some (or all) of the ten points as vertices? | ||
[[1989 AIME Problems/Problem 2|Solution]] | [[1989 AIME Problems/Problem 2|Solution]] | ||
== Problem 3 == | == Problem 3 == | ||
| + | Suppose <math>n_{}^{}</math> is a positive integer and <math>d_{}^{}</math> is a single digit in base 10. Find <math>n_{}^{}</math> if | ||
| + | <center><math>\frac{n}{810}=0.d25d25d25\ldots</math></center> | ||
[[1989 AIME Problems/Problem 3|Solution]] | [[1989 AIME Problems/Problem 3|Solution]] | ||
== Problem 4 == | == Problem 4 == | ||
| + | If <math>a<b<c<d<e^{}_{}</math> are consecutive positive integers such that <math>b+c+d</math> is a perfect square and <math>a+b+c+d+e^{}_{}</math> is a perfect cube, what is the smallest possible value of <math>c^{}_{}</math>? | ||
[[1989 AIME Problems/Problem 4|Solution]] | [[1989 AIME Problems/Problem 4|Solution]] | ||
== Problem 5 == | == Problem 5 == | ||
| + | When a certain biased coin is flipped five times, the probability of getting heads exactly once is not equal to <math>0</math> and is the same as that of getting heads exactly twice. Let <math>\frac ij^{}_{}</math>, in lowest terms, be the probability that the coin comes up heads in exactly <math>3</math> out of <math>5</math> flips. Find <math>i+j^{}_{}</math>. | ||
[[1989 AIME Problems/Problem 5|Solution]] | [[1989 AIME Problems/Problem 5|Solution]] | ||
== Problem 6 == | == Problem 6 == | ||
| + | Two skaters, Allie and Billie, are at points <math>A^{}_{}</math> and <math>B^{}_{}</math>, respectively, on a flat, frozen lake. The distance between <math>A^{}_{}</math> and <math>B^{}_{}</math> is <math>100^{}_{}</math> meters. Allie leaves <math>A^{}_{}</math> and skates at a speed of <math>8^{}_{}</math> meters per second on a straight line that makes a <math>60^\circ</math> angle with <math>AB^{}_{}</math>. At the same time Allie leaves <math>A^{}_{}</math>, Billie leaves <math>B^{}_{}</math> at a speed of <math>7^{}_{}</math> meters per second and follows the straight path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie? | ||
| + | <center><asy> | ||
| + | pointpen=black; pathpen=black+linewidth(0.7); | ||
| + | pair A=(0,0),B=(10,0),C=6*expi(pi/3); | ||
| + | D(B--A); D(A--C,EndArrow); MP("A",A,SW);MP("B",B,SE);MP("60^{\circ}",A+(0.3,0),NE);MP("100",(A+B)/2); | ||
| + | </asy></center><!-- Minsoen's image: [[Image:AIME_1989_Problem_6.png]] --> | ||
[[1989 AIME Problems/Problem 6|Solution]] | [[1989 AIME Problems/Problem 6|Solution]] | ||
== Problem 7 == | == Problem 7 == | ||
| − | + | If the integer <math>k^{}_{}</math> is added to each of the numbers <math>36^{}_{}</math>, <math>300^{}_{}</math>, and <math>596^{}_{}</math>, one obtains the squares of three consecutive terms of an arithmetic series. Find <math>k^{}_{}</math>. | |
[[1989 AIME Problems/Problem 7|Solution]] | [[1989 AIME Problems/Problem 7|Solution]] | ||
== Problem 8 == | == Problem 8 == | ||
| + | Assume that <math>x_1,x_2,\ldots,x_7</math> are real numbers such that | ||
| + | <cmath>\begin{align*} | ||
| + | x_1 + 4x_2 + 9x_3 + 16x_4 + 25x_5 + 36x_6 + 49x_7 &= 1, \ | ||
| + | 4x_1 + 9x_2 + 16x_3 + 25x_4 + 36x_5 + 49x_6 + 64x_7 &= 12, \ | ||
| + | 9x_1 + 16x_2 + 25x_3 + 36x_4 + 49x_5 + 64x_6 + 81x_7 &= 123. | ||
| + | \end{align*}</cmath> | ||
| + | Find the value of <math>16x_1+25x_2+36x_3+49x_4+64x_5+81x_6+100x_7</math>. | ||
[[1989 AIME Problems/Problem 8|Solution]] | [[1989 AIME Problems/Problem 8|Solution]] | ||
== Problem 9 == | == Problem 9 == | ||
| + | One of Euler's conjectures was disproved in the 1960s by three American mathematicians when they showed there was a positive integer such that <cmath>133^5+110^5+84^5+27^5=n^{5}.</cmath> Find the value of <math>n</math>. | ||
[[1989 AIME Problems/Problem 9|Solution]] | [[1989 AIME Problems/Problem 9|Solution]] | ||
== Problem 10 == | == Problem 10 == | ||
| + | Let <math>a</math>, <math>b</math>, <math>c</math> be the three sides of a triangle, and let <math>\alpha</math>, <math>\beta</math>, <math>\gamma</math>, be the angles opposite them. If <math>a^2+b^2=1989c^2</math>, find | ||
| + | <center><math>\frac{\cot \gamma}{\cot \alpha+\cot \beta}</math></center> | ||
[[1989 AIME Problems/Problem 10|Solution]] | [[1989 AIME Problems/Problem 10|Solution]] | ||
== Problem 11 == | == Problem 11 == | ||
| + | A sample of 121 integers is given, each between 1 and 1000 inclusive, with repetitions allowed. The sample has a unique mode (most frequent value). Let <math>D^{}_{}</math> be the difference between the mode and the arithmetic mean of the sample. What is the largest possible value of <math>\lfloor D^{}_{}\rfloor</math>? (For real <math>x^{}_{}</math>, <math>\lfloor x^{}_{}\rfloor</math> is the greatest integer less than or equal to <math>x^{}_{}</math>.) | ||
[[1989 AIME Problems/Problem 11|Solution]] | [[1989 AIME Problems/Problem 11|Solution]] | ||
== Problem 12 == | == Problem 12 == | ||
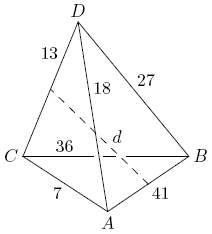
| + | Let <math>ABCD^{}_{}</math> be a tetrahedron with <math>AB=41^{}_{}</math>, <math>AC=7^{}_{}</math>, <math>AD=18^{}_{}</math>, <math>BC=36^{}_{}</math>, <math>BD=27^{}_{}</math>, and <math>CD=13^{}_{}</math>, as shown in the figure. Let <math>d^{}_{}</math> be the distance between the midpoints of edges <math>AB^{}_{}</math> and <math>CD^{}_{}</math>. Find <math>d^{2}_{}</math>. | ||
| + | |||
| + | [[Image:AIME_1989_Problem_12.png|center]] | ||
[[1989 AIME Problems/Problem 12|Solution]] | [[1989 AIME Problems/Problem 12|Solution]] | ||
== Problem 13 == | == Problem 13 == | ||
| + | Let <math>S^{}_{}</math> be a subset of <math>\{1,2,3^{}_{},\ldots,1989\}</math> such that no two members of <math>S^{}_{}</math> differ by <math>4^{}_{}</math> or <math>7^{}_{}</math>. What is the largest number of elements <math>S^{}_{}</math> can have? | ||
[[1989 AIME Problems/Problem 13|Solution]] | [[1989 AIME Problems/Problem 13|Solution]] | ||
== Problem 14 == | == Problem 14 == | ||
| + | Given a positive integer <math>n^{}_{}</math>, it can be shown that every complex number of the form <math>r+si^{}_{}</math>, where <math>r^{}_{}</math> and <math>s^{}_{}</math> are integers, can be uniquely expressed in the base <math>-n+i^{}_{}</math> using the integers <math>0,1,2^{}_{},\ldots,n^2</math> as digits. That is, the equation | ||
| + | <center><math>r+si=a_m(-n+i)^m+a_{m-1}(-n+i)^{m-1}+\cdots +a_1(-n+i)+a_0</math></center> | ||
| + | is true for a unique choice of non-negative integer <math>m^{}_{}</math> and digits <math>a_0,a_1^{},\ldots,a_m</math> chosen from the set <math>\{0^{}_{},1,2,\ldots,n^2\}</math>, with <math>a_m\ne 0^{}){}</math>. We write | ||
| + | <center><math>r+si=(a_ma_{m-1}\ldots a_1a_0)_{-n+i}</math></center> | ||
| + | to denote the base <math>-n+i^{}_{}</math> expansion of <math>r+si^{}_{}</math>. There are only finitely many integers <math>k+0i^{}_{}</math> that have four-digit expansions | ||
| + | <center><math>k=(a_3a_2a_1a_0)_{-3+i^{}_{}}~~~~a_3\ne 0.</math></center> | ||
| + | Find the sum of all such <math>k^{}_{}</math>. | ||
[[1989 AIME Problems/Problem 14|Solution]] | [[1989 AIME Problems/Problem 14|Solution]] | ||
== Problem 15 == | == Problem 15 == | ||
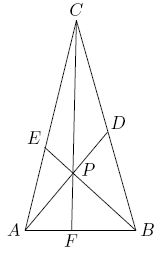
| + | Point <math>P</math> is inside <math>\triangle ABC</math>. Line segments <math>APD</math>, <math>BPE</math>, and <math>CPF</math> are drawn with <math>D</math> on <math>BC</math>, <math>E</math> on <math>AC</math>, and <math>F</math> on <math>AB</math> (see the figure below). Given that <math>AP=6</math>, <math>BP=9</math>, <math>PD=6</math>, <math>PE=3</math>, and <math>CF=20</math>, find the area of <math>\triangle ABC</math>. | ||
| + | [[Image:AIME_1989_Problem_15.png|center]] | ||
[[1989 AIME Problems/Problem 15|Solution]] | [[1989 AIME Problems/Problem 15|Solution]] | ||
== See also == | == See also == | ||
| + | |||
| + | {{AIME box|year=1989|before=[[1988 AIME Problems]]|after=[[1990 AIME Problems]]}} | ||
| + | |||
* [[American Invitational Mathematics Examination]] | * [[American Invitational Mathematics Examination]] | ||
* [[AIME Problems and Solutions]] | * [[AIME Problems and Solutions]] | ||
* [[Mathematics competition resources]] | * [[Mathematics competition resources]] | ||
| + | |||
| + | [[Category:AIME Problems|1989]] | ||
| + | {{MAA Notice}} | ||
Revision as of 19:47, 14 December 2023
| 1989 AIME (Answer Key) | AoPS Contest Collections • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
Contents
[hide]Problem 1
Compute ![]() .
.
Problem 2
Ten points are marked on a circle. How many distinct convex polygons of three or more sides can be drawn using some (or all) of the ten points as vertices?
Problem 3
Suppose ![]() is a positive integer and
is a positive integer and ![]() is a single digit in base 10. Find
is a single digit in base 10. Find ![]() if
if
Problem 4
If ![]() are consecutive positive integers such that
are consecutive positive integers such that ![]() is a perfect square and
is a perfect square and ![]() is a perfect cube, what is the smallest possible value of
is a perfect cube, what is the smallest possible value of ![]() ?
?
Problem 5
When a certain biased coin is flipped five times, the probability of getting heads exactly once is not equal to ![]() and is the same as that of getting heads exactly twice. Let
and is the same as that of getting heads exactly twice. Let ![]() , in lowest terms, be the probability that the coin comes up heads in exactly
, in lowest terms, be the probability that the coin comes up heads in exactly ![]() out of
out of ![]() flips. Find
flips. Find ![]() .
.
Problem 6
Two skaters, Allie and Billie, are at points ![]() and
and ![]() , respectively, on a flat, frozen lake. The distance between
, respectively, on a flat, frozen lake. The distance between ![]() and
and ![]() is
is ![]() meters. Allie leaves
meters. Allie leaves ![]() and skates at a speed of
and skates at a speed of ![]() meters per second on a straight line that makes a
meters per second on a straight line that makes a ![]() angle with
angle with ![]() . At the same time Allie leaves
. At the same time Allie leaves ![]() , Billie leaves
, Billie leaves ![]() at a speed of
at a speed of ![]() meters per second and follows the straight path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie?
meters per second and follows the straight path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie?
![[asy] pointpen=black; pathpen=black+linewidth(0.7); pair A=(0,0),B=(10,0),C=6*expi(pi/3); D(B--A); D(A--C,EndArrow); MP("A",A,SW);MP("B",B,SE);MP("60^{\circ}",A+(0.3,0),NE);MP("100",(A+B)/2); [/asy]](http://latex.artofproblemsolving.com/a/3/0/a30f95a4bc471ad519d35b683f2f319118167660.png)
Problem 7
If the integer ![]() is added to each of the numbers
is added to each of the numbers ![]() ,
, ![]() , and
, and ![]() , one obtains the squares of three consecutive terms of an arithmetic series. Find
, one obtains the squares of three consecutive terms of an arithmetic series. Find ![]() .
.
Problem 8
Assume that ![]() are real numbers such that
are real numbers such that
 Find the value of
Find the value of ![]() .
.
Problem 9
One of Euler's conjectures was disproved in the 1960s by three American mathematicians when they showed there was a positive integer such that ![]() Find the value of
Find the value of ![]() .
.
Problem 10
Let ![]() ,
, ![]() ,
, ![]() be the three sides of a triangle, and let
be the three sides of a triangle, and let ![]() ,
, ![]() ,
, ![]() , be the angles opposite them. If
, be the angles opposite them. If ![]() , find
, find
Problem 11
A sample of 121 integers is given, each between 1 and 1000 inclusive, with repetitions allowed. The sample has a unique mode (most frequent value). Let ![]() be the difference between the mode and the arithmetic mean of the sample. What is the largest possible value of
be the difference between the mode and the arithmetic mean of the sample. What is the largest possible value of ![]() ? (For real
? (For real ![]() ,
, ![]() is the greatest integer less than or equal to
is the greatest integer less than or equal to ![]() .)
.)
Problem 12
Let ![]() be a tetrahedron with
be a tetrahedron with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , as shown in the figure. Let
, as shown in the figure. Let ![]() be the distance between the midpoints of edges
be the distance between the midpoints of edges ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 13
Let ![]() be a subset of
be a subset of ![]() such that no two members of
such that no two members of ![]() differ by
differ by ![]() or
or ![]() . What is the largest number of elements
. What is the largest number of elements ![]() can have?
can have?
Problem 14
Given a positive integer ![]() , it can be shown that every complex number of the form
, it can be shown that every complex number of the form ![]() , where
, where ![]() and
and ![]() are integers, can be uniquely expressed in the base
are integers, can be uniquely expressed in the base ![]() using the integers
using the integers ![]() as digits. That is, the equation
as digits. That is, the equation
is true for a unique choice of non-negative integer ![]() and digits
and digits ![]() chosen from the set
chosen from the set ![]() , with
, with ![]() . We write
. We write
to denote the base ![]() expansion of
expansion of ![]() . There are only finitely many integers
. There are only finitely many integers ![]() that have four-digit expansions
that have four-digit expansions
Find the sum of all such ![]() .
.
Problem 15
Point ![]() is inside
is inside ![]() . Line segments
. Line segments ![]() ,
, ![]() , and
, and ![]() are drawn with
are drawn with ![]() on
on ![]() ,
, ![]() on
on ![]() , and
, and ![]() on
on ![]() (see the figure below). Given that
(see the figure below). Given that ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , find the area of
, find the area of ![]() .
.
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by 1988 AIME Problems |
Followed by 1990 AIME Problems | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
- American Invitational Mathematics Examination
- AIME Problems and Solutions
- Mathematics competition resources
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()