1990 AIME Problems
| 1990 AIME (Answer Key) | AoPS Contest Collections • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
Contents
[hide]Problem 1
The increasing sequence ![]() consists of all positive integers that are neither the square nor the cube of a positive integer. Find the 500th term of this sequence.
consists of all positive integers that are neither the square nor the cube of a positive integer. Find the 500th term of this sequence.
Problem 2
Find the value of ![]() .
.
Problem 3
Let ![]() be a regular
be a regular ![]() and
and ![]() be a regular
be a regular ![]()
![]() such that each interior angle of
such that each interior angle of ![]() is
is ![]() as large as each interior angle of
as large as each interior angle of ![]() . What's the largest possible value of
. What's the largest possible value of ![]() ?
?
Problem 4
Find the positive solution to
Problem 5
Let ![]() be the smallest positive integer that is a multiple of
be the smallest positive integer that is a multiple of ![]() and has exactly
and has exactly ![]() positive integral divisors, including
positive integral divisors, including ![]() and itself. Find
and itself. Find ![]() .
.
Problem 6
A biologist wants to calculate the number of fish in a lake. On May 1 she catches a random sample of 60 fish, tags them, and releases them. On September 1 she catches a random sample of 70 fish and finds that 3 of them are tagged. To calculate the number of fish in the lake on May 1, she assumes that 25% of these fish are no longer in the lake on September 1 (because of death and emigrations), that 40% of the fish were not in the lake May 1 (because of births and immigrations), and that the number of untagged fish and tagged fish in the September 1 sample are representative of the total population. What does the biologist calculate for the number of fish in the lake on May 1?
Problem 7
A triangle has vertices ![]() ,
, ![]() , and
, and ![]() . The equation of the bisector of
. The equation of the bisector of ![]() can be written in the form
can be written in the form ![]() . Find
. Find ![]() .
.
Problem 8
In a shooting match, eight clay targets are arranged in two hanging columns of three targets each and one column of two targets. A marksman is to break all the targets according to the following rules:
1) The marksman first chooses a column from which a target is to be broken.
2) The marksman must then break the lowest remaining target in the chosen column.
If the rules are followed, in how many different orders can the eight targets be broken?
Problem 9
A fair coin is to be tossed ![]() times. Let
times. Let ![]() , in lowest terms, be the probability that heads never occur on consecutive tosses. Find
, in lowest terms, be the probability that heads never occur on consecutive tosses. Find ![]() .
.
Problem 10
The sets ![]() and
and ![]() are both sets of complex roots of unity. The set
are both sets of complex roots of unity. The set ![]() is also a set of complex roots of unity. How many distinct elements are in
is also a set of complex roots of unity. How many distinct elements are in ![]() ?
?
Problem 11
Someone observed that ![]() . Find the largest positive integer
. Find the largest positive integer ![]() for which
for which ![]() can be expressed as the product of
can be expressed as the product of ![]() consecutive positive integers.
consecutive positive integers.
Problem 12
A regular 12-gon is inscribed in a circle of radius 12. The sum of the lengths of all sides and diagonals of the 12-gon can be written in the form
where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
Problem 13
Let ![]() . Given that
. Given that ![]() has 3817 digits and that its first (leftmost) digit is 9, how many elements of
has 3817 digits and that its first (leftmost) digit is 9, how many elements of ![]() have 9 as their leftmost digit?
have 9 as their leftmost digit?
Problem 14
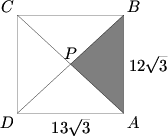
The rectangle ![]() below has dimensions
below has dimensions ![]() and
and ![]() . Diagonals
. Diagonals ![]() and
and ![]() intersect at
intersect at ![]() . If triangle
. If triangle ![]() is cut out and removed, edges
is cut out and removed, edges ![]() and
and ![]() are joined, and the figure is then creased along segments
are joined, and the figure is then creased along segments ![]() and
and ![]() , we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
, we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
Problem 15
Find ![]() if the real numbers
if the real numbers ![]() and
and ![]() satisfy the equations
satisfy the equations

See also
| 1990 AIME (Problems • Answer Key • Resources) | ||
| Preceded by 1989 AIME Problems |
Followed by 1991 AIME Problems | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
- American Invitational Mathematics Examination
- AIME Problems and Solutions
- Mathematics competition resources
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()