Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2006 Cyprus MO/Lyceum/Problem 18"

(solution)
(Standardized answer choices; minor edits to solution)
 
(One intermediate revision by one other user not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
<div style="float:right">
+
[[Image:2006 CyMO-18.PNG|250px|right]]
−
[[Image:2006 CyMO-18.PNG|250px]]
 
−
</div>
 
  
−
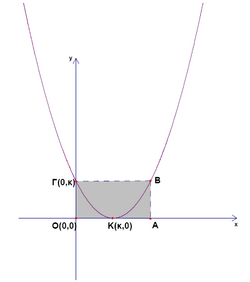
<math>K(k,0)</math> is the minimum point of the parabola and the parabola intersects the y-axis at the point <math>C(0,k)</math>.
+
<math>K(k,0)</math> is the minimum point of the parabola and the parabola intersects the y-axis at the point <math>\Gamma (0,k)</math>.
−
If the area if the rectangle <math>OABC</math> is <math>8</math>, then the equation of the parabola is
+
If the area if the rectangle <math>OAB\Gamma</math> is <math>8</math>, then the equation of the parabola is
  
−
A. <math>y=\frac{1}{2}(x+2)^2</math>
+
<math>\mathrm{(A)}\ y=\frac{1}{2}(x+2)^2\qquad\mathrm{(B)}\ y=\frac{1}{2}(x-2)^2\qquad\mathrm{(C)}\ y=x^2+2\qquad\mathrm{(D)}\ y=x^2-2x+1\qquad\mathrm{(E)}\ y=x^2-4x+4</math>
  
−
B. <math>y=\frac{1}{2}(x-2)^2</math>
+
==Solution==
 +
Since the parabola is symmetric about the line <math>x = k</math>, <math>B</math> has coordinates <math>(2k,k)</math>. The area of the rectangle is <math>k \cdot 2k = 8 \Longrightarrow k = 2</math>, so the vertex is at <math>(2,0)</math>.
  
−
C. <math>y=x^2+2</math>
+
Thus, the equation of the parabola is <math>y = a(x-2)^2</math>. Plugging in point <math>(0,2)</math>, we find <math>a = \frac{1}{2}</math>, and the answer is <math>\mathrm{B}</math>.
−
 
 
−
D. <math>y=x^2-2x+1</math>
 
−
 
 
−
E. <math>y=x^2-4x+4</math>
 
−
 
 
−
==Solution==
 
−
Since the parabola is symmetric about the line <math>x = k</math>, <math>B</math> has coordinates <math>(2k,k)</math>. The area of the rectangle is <math>k \cdot 2k = 8 \Longrightarrow k = 2</math>, so the vertex is at <math>(2,0)</math>. Thus the equation of the parabola is <math>y = a(x-2)^2</math>, and plugging in point <math>(0,2)</math> and finding <math>a = \frac{1}{2}</math>, the answer is <math>\mathrm{B}</math>.
 
  
 
==See also==
 
==See also==

Latest revision as of 12:39, 26 April 2008

Problem

2006 CyMO-18.PNG

$K(k,0)$ is the minimum point of the parabola and the parabola intersects the y-axis at the point $\Gamma (0,k)$. If the area if the rectangle $OAB\Gamma$ is $8$, then the equation of the parabola is

$\mathrm{(A)}\ y=\frac{1}{2}(x+2)^2\qquad\mathrm{(B)}\ y=\frac{1}{2}(x-2)^2\qquad\mathrm{(C)}\ y=x^2+2\qquad\mathrm{(D)}\ y=x^2-2x+1\qquad\mathrm{(E)}\ y=x^2-4x+4$

Solution

Since the parabola is symmetric about the line $x = k$, $B$ has coordinates $(2k,k)$. The area of the rectangle is $k \cdot 2k = 8 \Longrightarrow k = 2$, so the vertex is at $(2,0)$.

Thus, the equation of the parabola is $y = a(x-2)^2$. Plugging in point $(0,2)$, we find $a = \frac{1}{2}$, and the answer is $\mathrm{B}$.

See also

2006 Cyprus MO, Lyceum (Problems)
Preceded by
Problem 17 		Followed by
Problem 19
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2006_Cyprus_MO/Lyceum/Problem_18&oldid=25569"