Difference between revisions of "2004 AMC 12A Problems/Problem 13"
m (wik) |
(→See also) |
||
| Line 24: | Line 24: | ||
[[Category:Intermediate Combinatorics Problems]] | [[Category:Intermediate Combinatorics Problems]] | ||
| + | http://www.artofproblemsolving.com/Wiki/index.php?title=2004_AMC_12A_Problems/Problem_14&action=edit§ion=3 | ||
Revision as of 19:18, 3 July 2013
Problem
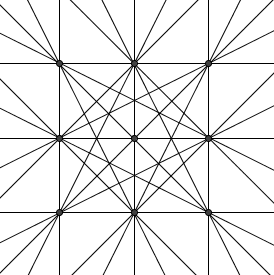
Let ![]() be the set of points
be the set of points ![]() in the coordinate plane, where each of
in the coordinate plane, where each of ![]() and
and ![]() may be
may be ![]() ,
, ![]() , or
, or ![]() . How many distinct lines pass through at least two members of
. How many distinct lines pass through at least two members of ![]() ?
?
![]()
Contents
[hide]Solution
Solution 1
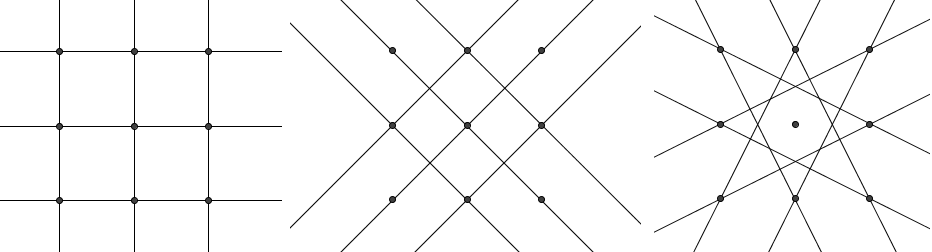
Let's count them by cases:
- Case 1: The line is horizontal or vertical, clearly
 .
. - Case 2: The line has slope
 , with
, with  through
through  and
and  additional ones one unit above or below those. These total
additional ones one unit above or below those. These total  .
. - Case 3: The only remaining lines pass through two points, a vertex and a non-vertex point on the opposite side. Thus we have each vertex pairing up with two points on the two opposites sides, giving
 lines.
lines.
These add up to ![]() .
.
Solution 2
There are  ways to pick two points, but we've clearly overcounted all of the lines which pass through three points. In fact, each line which passes through three points will have been counted
ways to pick two points, but we've clearly overcounted all of the lines which pass through three points. In fact, each line which passes through three points will have been counted  times, so we have to subtract
times, so we have to subtract ![]() for each of these lines. Quick counting yields
for each of these lines. Quick counting yields ![]() horizontal,
horizontal, ![]() vertical, and
vertical, and ![]() diagonal lines, so the answer is
diagonal lines, so the answer is ![]() distinct lines.
distinct lines.
See also
| 2004 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |