Difference between revisions of "2020 AIME II Problems/Problem 13"

Latest revision as of 22:00, 8 January 2024

Problem

Convex pentagon $ABCDE$ has side lengths $AB=5$ , $BC=CD=DE=6$ , and $EA=7$ . Moreover, the pentagon has an inscribed circle (a circle tangent to each side of the pentagon). Find the area of $ABCDE$ .

Solution 1

Assume the incircle touches $AB$ , $BC$ , $CD$ , $DE$ , $EA$ at $P,Q,R,S,T$ respectively. Then let $PB=x=BQ=RD=SD$ , $ET=y=ES=CR=CQ$ , $AP=AT=z$ . So we have $x+y=6$ , $x+z=5$ and $y+z$ =7, solve it we have $x=2$ , $z=3$ , $y=4$ . Let the center of the incircle be $I$ , by SAS we can proof triangle $BIQ$ is congruent to triangle $DIS$ , and triangle $CIR$ is congruent to triangle $SIE$ . Then we have $\angle AED=\angle BCD$ , $\angle ABC=\angle CDE$ . Extend $CD$ , cross ray $AB$ at $M$ , ray $AE$ at $N$ , then by AAS we have triangle $END$ is congruent to triangle $BMC$ . Thus $\angle M=\angle N$ . Let $EN=MC=a$ , then $BM=DN=a+2$ . So by law of cosine in triangle $END$ and triangle $ANM$ we can obtain $\frac{2a+8}{2(a+7)}=\cos N=\frac{a^2+(a+2)^2-36}{2a(a+2)}$ , solved it gives us $a=8$ , which yield triangle $ANM$ to be a triangle with side length 15, 15, 24, draw a height from $A$ to $NM$ divides it into two triangles with side lengths 9, 12, 15, so the area of triangle $ANM$ is 108. Triangle $END$ is a triangle with side lengths 6, 8, 10, so the area of two of them is 48, so the area of pentagon is $108-48=\boxed{60}$ .

-Fanyuchen20020715

Solution 2 (Complex Bash)

Suppose that the circle intersects $\overline{AB}$ , $\overline{BC}$ , $\overline{CD}$ , $\overline{DE}$ , and $\overline{EA}$ at $P$ , $Q$ , $R$ , $S$ , and $T$ respectively. Then $AT = AP = a$ , $BP = BQ = b$ , $CQ = CR = c$ , $DR = DS = d$ , and $ES = ET = e$ . So $a + b = 5$ , $b + c = 6$ , $c + d = 6$ , $d + e = 6$ , and $e + a = 7$ . Then $2a + 2b + 2c + 2d + 2e = 30$ , so $a + b + c + d + e= 15$ . Then we can solve for each individually. $a = 3$ , $b = 2$ , $c = 4$ , $d = 2$ , and $e = 4$ . To find the radius, we notice that $4 \arctan(\frac{2}{r}) + 4 \arctan(\frac{4}{r}) + 2 \arctan (\frac{3}{r}) = 360 ^ \circ$ , or $2 \arctan(\frac{2}{r}) + 2 \arctan(\frac{4}{r}) + \arctan (\frac{3}{r}) = 180 ^ \circ$ . Each of these angles in this could be represented by complex numbers. When two complex numbers are multiplied, their angles add up to create the angle of the resulting complex number. Thus, $(r + 2i)^2 \cdot (r + 4i)^2 \cdot (r + 3i)$ is real. Expanding, we get:

$(r^2 + 4ir - 4)(r^2 + 8ir -16)(r + 3i)$

$(r^4 + 12ir^3 - 52r^2 - 96ir + 64)(r + 3i)$

On the last expanding, we only multiply the reals with the imaginaries and vice versa, because we only care that the imaginary component equals 0.

$15ir^4 - 252ir^2 + 192i = 0$

$5r^4 - 84r^2 + 64 = 0$

$(5r^2 - 4)(r^2 - 16) = 0$

$r$ must equal 4, as r cannot be negative or be approximately equal to 1. Thus, the area of $ABCDE$ is $4 \cdot (a + b + c + d + e) = 4 \cdot 15 = \boxed{60}$

-nihao4112

Solution 3 (Guess 1)

This pentagon is very close to a regular pentagon with side lengths $6$ . The area of a regular pentagon with side lengths $s$ is $\frac{5s^2}{4\sqrt{5-2\sqrt{5}}}$ . $5-2\sqrt{5}$ is slightly greater than $\frac{1}{2}$ given that $2\sqrt{5}$ is slightly less than $\frac{9}{2}$ . $4\sqrt{5-2\sqrt{5}}$ is then slightly greater than $2\sqrt{2}$ . We will approximate that to be $2.9$ . The area is now roughly $\frac{180}{2.9}$ , but because the actual pentagon is not regular, but has the same perimeter of the regular one that we are comparing to we can say that this is an overestimate on the area and turn the $2.9$ into $3$ thus turning the area into $\frac{180}{3}$ which is $60$ and since $60$ is a multiple of the semiperimeter $15$ , we can safely say that the answer is most likely $\boxed{60}$ .

~Lopkiloinm

Solution 4 (Guess 2)

Because the AIME answers have to be a whole number it would meant the radius of the circle have to be a whole number, thus by drawing the diagram and experimenting, we can safely say the radius is 4 and the answer is 60

(Edit: While the guess would be technically correct, the assumption that the radius would have to be a whole number for the ans to be a whole number is wrong)

By EtherealMidnight

(Edit: I think that will actually work because the area of $ABCDE$ is equal to the semi-perimeter times the radius. By a simple calculation, we know that the semi-perimeter is an integer so the radius should also be an integer)

By YBSuburbanTea

...the radius could be a fraction with denominator 3, 5, or 15, and the area of the pentagon would still be an integer. - GeometryJake

Solution 5 (Official MAA 1)

Let $\omega$ be the inscribed circle, $I$ be its center, and $r$ be its radius. The area of $ABCDE$ is equal to its semiperimeter, $15,$ times $r$ , so the problem is reduced to finding $r$ . Let $a$ be the length of the tangent segment from $A$ to $\omega$ , and analogously define $b$ , $c$ , $d$ , and $e$ . Then $a+b=5$ , $b+c= c+d=d+e=6$ , and $e+a=7$ , with a total of $a+b+c+d+e=15$ . Hence $a=3$ , $b=d=2$ , and $c=e=4$ . It follows that $\angle B= \angle D$ and $\angle C= \angle E$ . Let $Q$ be the point where $\omega$ is tangent to $\overline{CD}$ . Then $\angle IAE = \angle IAB =\frac{1}{2}\angle A$ . Now we claim that points $A, I, Q$ are collinear, which can be proved if $\angle{AIQ}=\angle{QIA}=180^{\circ}$ . The sum of the internal angles in polygons $ABCQI$ and $AIQDE$ are equal, so $\angle IAE + \angle AIQ + \angle IQD + \angle D + \angle E = \angle IAB + \angle B + \angle C + \angle CQI + \angle QIA$ , which implies that $\angle AIQ$ must be $180^\circ$ . Therefore points $A$ , $I$ , and $Q$ are collinear. $[asy] defaultpen(fontsize(8pt)); unitsize(0.025cm); pair[] vertices = {(0,0), (5,0), (8.6,4.8), (3.8,8.4), (-1.96, 6.72)}; string[] labels = {"$A$", "$B$", "$C$", "$D$", "$E$"}; pair[] dirs = {SW, SE,E, N, NW}; string[] smallLabels = {"$a$", "$b$", "$c$", "$d$", "$e$"}; pair I = (3,4); real rad = 4; pair Q = foot(I, vertices[2], vertices[3]); pair[] interpoints = {}; for(int i =0; i<vertices.length; ++i){ interpoints.push(foot(I, vertices[i], vertices[(i+1)%vertices.length])); } for(int i = 0; i< vertices.length; ++i){ draw(vertices[i]--vertices[(i+1)%vertices.length]); dot(labels[i],vertices[i],dirs[i]); draw(I--vertices[i]); } draw(Circle(I, rad)); dot("$I$", I, dir(200)); draw(I--Q); dot("$Q$", Q, NE); for(int i = 0; i < vertices.length; ++i){ label(smallLabels[i], vertices[i] --interpoints[i]); //dot(interpoints[i], blue); label(smallLabels[i], interpoints[(i-1)%vertices.length] -- vertices[i]); } [/asy]$ Because $\overline{AQ} \perp \overline{CD}$ , it follows that $AC^2-AD^2=CQ^2-DQ^2=c^2-d^2=12.$ Another expression for $AC^2-AD^2$ can be found as follows. Note that $\tan \left(\frac{\angle B}{2}\right) = \frac{r}{2}$ and $\tan \left(\frac{\angle E}{2}\right) = \frac{r}{4}$ , so $\cos (\angle B) =\frac{1-\tan^2 \left(\frac{\angle B}{2}\right)}{1+\tan^2 \left(\frac{\angle B}{2}\right)} = \frac{4-r^2}{4+r^2}$ and $\cos (\angle E) = \frac{1-\tan^2 \left(\frac{\angle E}{2}\right)}{1+\tan^2 \left(\frac{\angle E}{2}\right)}= \frac{16-r^2}{16+r^2}.$ Applying the Law of Cosines to $\triangle ABC$ and $\triangle AED$ gives $AC^2=AB^2+BC^2-2\cdot AB\cdot BC\cdot \cos (\angle B) = 5^2+6^2-2 \cdot 5 \cdot 6 \cdot \frac{4-r^2}{4+r^2}$ and $AD^2=AE^2+DE^2-2 \cdot AE \cdot DE \cdot \cos(\angle E) = 7^2+6^2-2 \cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2}.$ Hence

$12=AC^2- AD^2= 5^2-2\cdot 5 \cdot 6\cdot \frac{4-r^2}{4+r^2} -7^2+2\cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2},$ yielding $2\cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2}- 2\cdot 5 \cdot 6\cdot \frac{4-r^2}{4+r^2}= 36;$ equivalently $7(16-r^2)(4+r^2)-5(4-r^2)(16+r^2) = 3(16+r^2)(4+r^2).$ Substituting $x=r^2$ gives the quadratic equation $5x^2-84x+64=0$ , with solutions $\frac{42 - 38}{5}=\frac45$ , and $\frac{42 + 38}{5}= 16$ . The solution $r^2=\frac45$ corresponds to a five-pointed star, which is not convex. Indeed, if $r<3$ , then $\tan \left(\frac{\angle A}{2}\right)$ , $\tan \left(\frac{\angle C}{2}\right)$ , and $\tan \left(\frac{\angle E}{2}\right)$ are less than $1,$ implying that $\angle A$ , $\angle C$ , and $\angle E$ are acute, which cannot happen in a convex pentagon. Thus $r^2=16$ and $r=4$ . The requested area is $15\cdot4 = \boxed{60}$ .

Solution 6 (Official MAA 2)

Define $a$ , $b$ , $c$ , $d$ , $e$ , and $r$ as in Solution 5. Then, as in Solution 5, $a=3$ , $b=d=2$ , $c=e=4$ , $\angle B= \angle D$ , and $\angle C= \angle E$ . Let $\alpha =\frac{\angle A}{2}$ , $\beta = \frac{\angle B}{2}$ , and $\gamma=\frac{\angle C}{2}$ . It follows that $540^{\circ} = 2\alpha + 4 \beta + 4 \gamma$ , so $270^{\circ} = \alpha + 2\beta + 2 \gamma$ . Thus $\tan(2\beta + 2 \gamma) = \frac{1}{\tan \alpha},$ $\tan(\beta) = \frac{r}{2}$ , $\tan(\gamma) = \frac{r}{4}$ , and $\tan(\alpha) = \frac {r}{3}$ . By the Tangent Addition Formula, $\tan(\beta +\gamma) = \frac{6r}{8-r^2}$ and $\tan(2\beta + 2\gamma) = \frac{\frac{12r}{8-r^2}}{1-\frac{36r^2}{(8-r^2)^2}} = \frac{12r(8-r^2)}{(8-r^2)^2-36r^2}.$ Therefore $\frac{12r(8-r^2)}{(8-r^2)^2-36r^2} = \frac{3}{r},$ which simplifies to $5r^4 - 84r^2 + 64 = 0$ . Then the solution proceeds as in Solution 5.

Solution 7 (Official MAA 3)

Define $a$ , $b$ , $c$ , $d$ , $e$ , and $r$ as in Solution 5. Note that $\arctan\left(\frac{a}{r}\right) + \arctan\left(\frac{b}{r}\right) + \arctan\left(\frac{c}{r}\right) + \arctan\left(\frac{d}{r}\right) + \arctan\left(\frac{e}{r}\right) = 180^{\circ}.$ Hence $\operatorname{Arg}(r + 3i) + 2\cdot \operatorname{Arg}(r + 2i) + 2\cdot \operatorname{Arg}(r + 4i) = 180^{\circ}.$ Therefore $\operatorname{Im} \big( (r + 3i)(r+2i)^2(r+4i)^2 \big) = 0.$ Simplifying this equation gives the same quadratic equation in $r^2$ as in Solution 5.

Solution 8 (The same circle)

Notation shown on diagram. As in solution 5, we get $\overline{AQ} \perp \overline{CD}, AG = 3, GB = 2, CQ = 4$ and so on.

Let $\overline{AB}$ cross $\overline{CD}$ at $F, \overline{AE}$ cross $\overline{CD}$ at $F', CF = x.$ $FQ = FG \implies FB = x+2.$ $\angle BAQ = \angle EAQ \implies DF' = x + 2, EF' = x.$ Triangle $\triangle AFF'$ has semiperimeter $s = 2x + 11.$

The radius of incircle $\omega$ is $r =\sqrt{\frac{s-FF’}{s}}(s-AF) = \sqrt{\frac{3}{2x +11}}(x+4).$

Triangle $\triangle BCF$ has semiperimeter $s = x + 4.$

The radius of excircle $\omega$ is $r = \sqrt{\frac{s(s-BF)(s-CF)}{s-BC}} = \sqrt{ \frac{(x+4)\cdot 2 \cdot 4}{x - 2}}.$

It is the same radius, therefore $\sqrt{\frac{3}{2x +11}}(x+4) = \sqrt{\frac{8(x+4)}{x – 2}} \implies \frac {3(x+4)}{2x+11} = \frac {8}{x-2} \implies (x-8)(3x + 14) = 0 \implies x = 8, r = 4.$

Then the solution proceeds as in Solution 5.

vladimir.shelomovskii@gmail.com, vvsss

Video Solution 1 by MOP 2024

https://youtube.com/watch?v=BXEXcCNXrlM

~r00tsOfUnity

Video Solution 2

https://youtu.be/bz5N-jI2e0U?t=327

Video Solution 3

https://youtu.be/_fwkGTdMd8U

Video Solution 4

https://youtu.be/kn3c2LStiHA (solve in 5 minutes)

~MathProblemSolvingSkills.com

2020 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.

@@ Line 2: / Line 2: @@
 Convex pentagon <math>ABCDE</math> has side lengths <math>AB=5</math>, <math>BC=CD=DE=6</math>, and <math>EA=7</math>. Moreover, the pentagon has an inscribed circle (a circle tangent to each side of the pentagon). Find the area of <math>ABCDE</math>.
-==Solution 1 (Misplaced problem?)==
+==Solution 1==
 Assume the incircle touches <math>AB</math>, <math>BC</math>, <math>CD</math>, <math>DE</math>, <math>EA</math> at <math>P,Q,R,S,T</math> respectively. Then let <math>PB=x=BQ=RD=SD</math>, <math>ET=y=ES=CR=CQ</math>, <math>AP=AT=z</math>. So we have <math>x+y=6</math>, <math>x+z=5</math> and <math>y+z</math>=7, solve it we have <math>x=2</math>, <math>z=3</math>, <math>y=4</math>. Let the center of the incircle be <math>I</math>, by SAS we can proof triangle <math>BIQ</math> is congruent to triangle <math>DIS</math>, and triangle <math>CIR</math> is congruent to triangle <math>SIE</math>. Then we have <math>\angle AED=\angle BCD</math>, <math>\angle ABC=\angle CDE</math>. Extend <math>CD</math>, cross ray <math>AB</math> at <math>M</math>, ray <math>AE</math> at <math>N</math>, then by AAS we have triangle <math>END</math> is congruent to triangle <math>BMC</math>. Thus <math>\angle M=\angle N</math>. Let <math>EN=MC=a</math>, then <math>BM=DN=a+2</math>. So by law of cosine in triangle <math>END</math> and triangle <math>ANM</math> we can obtain <cmath>\frac{2a+8}{2(a+7)}=\cos N=\frac{a^2+(a+2)^2-36}{2a(a+2)}</cmath>, solved it gives us <math>a=8</math>, which yield triangle <math>ANM</math> to be a triangle with side length 15, 15, 24, draw a height from <math>A</math> to <math>NM</math> divides it into two triangles with side lengths 9, 12, 15, so the area of triangle <math>ANM</math> is 108. Triangle <math>END</math> is a triangle with side lengths 6, 8, 10, so the area of two of them is 48, so the area of pentagon is <math>108-48=\boxed{60}</math>.
@@ Line 9: / Line 9: @@
 ==Solution 2 (Complex Bash)==
 Suppose that the circle intersects <math>\overline{AB}</math>, <math>\overline{BC}</math>, <math>\overline{CD}</math>, <math>\overline{DE}</math>, and <math>\overline{EA}</math> at <math>P</math>, <math>Q</math>, <math>R</math>, <math>S</math>, and <math>T</math> respectively. Then <math>AT = AP = a</math>, <math>BP = BQ = b</math>, <math>CQ = CR = c</math>, <math>DR = DS = d</math>, and <math>ES = ET = e</math>. So <math>a + b = 5</math>, <math>b + c = 6</math>, <math>c + d = 6</math>, <math>d + e = 6</math>, and <math>e + a = 7</math>. Then <math>2a + 2b + 2c + 2d + 2e = 30</math>, so <math>a + b + c + d + e= 15</math>. Then we can solve for each individually. <math>a = 3</math>, <math>b = 2</math>, <math>c = 4</math>, <math>d = 2</math>, and <math>e = 4</math>. To find the radius, we notice that <math>4 \arctan(\frac{2}{r}) + 4 \arctan(\frac{4}{r}) + 2 \arctan (\frac{3}{r}) = 360 ^ \circ</math>, or <math>2 \arctan(\frac{2}{r}) + 2 \arctan(\frac{4}{r}) + \arctan (\frac{3}{r}) = 180 ^ \circ</math>. Each of these angles in this could be represented by complex numbers. When two complex numbers are multiplied, their angles add up to create the angle of the resulting complex number. Thus, <math>(r + 2i)^2 \cdot (r + 4i)^2 \cdot (r + 3i)</math> is real. Expanding, we get:
-<math>(r^2 + 4ir - 4)(r^2 + 8ir -16)(r + 3i)</math>, then
-<math>(r^4 + 12ir^3 - 52r^2 - 96ir + 64)(r + 3i)</math>.
+<cmath>(r^2 + 4ir - 4)(r^2 + 8ir -16)(r + 3i)</cmath>
+<cmath>(r^4 + 12ir^3 - 52r^2 - 96ir + 64)(r + 3i)</cmath>
 On the last expanding, we only multiply the reals with the imaginaries and vice versa, because we only care that the imaginary component equals 0.
-<math>15ir^4 - 252ir^2 + 192i = 0</math>.
-<math>5r^4 - 84r^2 + 64 = 0</math>
+<cmath>15ir^4 - 252ir^2 + 192i = 0</cmath>
-<math>(5r^2 - 4)(r^2 - 16) = 0</math>.
+<cmath>5r^4 - 84r^2 + 64 = 0</cmath>
+<cmath>(5r^2 - 4)(r^2 - 16) = 0</cmath>
 <math>r</math> must equal 4, as r cannot be negative or be approximately equal to 1.
 Thus, the area of <math>ABCDE</math> is <math>4 \cdot (a + b + c + d + e) = 4 \cdot 15 = \boxed{60}</math>
@@ Line 20: / Line 27: @@
 -nihao4112
-==Solution 3 (Guess)==
+==Solution 3 (Guess 1)==
 This pentagon is very close to a regular pentagon with side lengths <math>6</math>. The area of a regular pentagon with side lengths <math>s</math> is <math>\frac{5s^2}{4\sqrt{5-2\sqrt{5}}}</math>. <math>5-2\sqrt{5}</math> is slightly greater than <math>\frac{1}{2}</math> given that <math>2\sqrt{5}</math> is slightly less than <math>\frac{9}{2}</math>. <math>4\sqrt{5-2\sqrt{5}}</math> is then slightly greater than <math>2\sqrt{2}</math>. We will approximate that to be <math>2.9</math>. The area is now roughly <math>\frac{180}{2.9}</math>, but because the actual pentagon is not regular, but has the same perimeter of the regular one that we are comparing to we can say that this is an overestimate on the area and turn the <math>2.9</math> into <math>3</math> thus turning the area into <math>\frac{180}{3}</math> which is <math>60</math> and since <math>60</math> is a multiple of the semiperimeter <math>15</math>, we can safely say that the answer is most likely <math>\boxed{60}</math>.
 ~Lopkiloinm
-==Solution 4 (Official MAA 1)==
+==Solution 4 (Guess 2)==
-Let <math>\omega</math> be the inscribed circle, <math>I</math> be its center, and <math>r</math> be its radius. The area of <math>ABCDE</math> is equal to its semiperimeter, <math>15,</math> times <math>r</math>, so the problem is reduced to finding <math>r</math>. Let <math>a</math> be the length of the tangent segment from <math>A</math> to <math>\omega</math>, and analogously define <math>b</math>, <math>c</math>, <math>d</math>, and <math>e</math>. Then <math>a+b=5</math>, <math>b+c= c+d=d+e=6</math>, and <math>e+a=7</math>, with a total of <math>a+b+c+d+e=15</math>. Hence <math>a=3</math>, <math>b=d=2</math>, and <math>c=e=4</math>. It follows that <math>\angle B= \angle D</math> and <math>\angle C= \angle E</math>. Let <math>Q</math> be the point where <math>\omega</math> is tangent to <math>\overline{CD}</math>. Then <math>\angle IAE = \angle IAB =\frac{1}{2}\angle A</math>. The sum of the internal angles in polygons <math>ABCQI</math> and <math>AIQDE</math> are equal, so <math>\angle IAE + \angle AIQ + \angle IQD + \angle D + \angle E = \angle IAB + \angle B + \angle C + \angle CQI + \angle QIA</math>, which implies that <math>\angle AIQ</math> must be <math>180^\circ</math>. Therefore points <math>A</math>, <math>I</math>, and <math>Q</math> are collinear.
+Because the AIME answers have to be a whole number it would meant the radius of the circle have to be a whole number, thus by drawing the diagram and experimenting, we can safely say the radius is 4 and the answer is 60
+(Edit: While the guess would be technically correct, the assumption that the radius would have to be a whole number for the ans to be a whole number is wrong)
+By EtherealMidnight
+(Edit: I think that will actually work because the area of <math>ABCDE</math> is equal to the semi-perimeter times the radius. By a simple calculation, we know that the semi-perimeter is an integer so the radius should also be an integer)
+By YBSuburbanTea
+...the radius could be a fraction with denominator 3, 5, or 15, and the area of the pentagon would still be an integer. - GeometryJake
+==Solution 5 (Official MAA 1)==
+Let <math>\omega</math> be the inscribed circle, <math>I</math> be its center, and <math>r</math> be its radius. The area of <math>ABCDE</math> is equal to its semiperimeter, <math>15,</math> times <math>r</math>, so the problem is reduced to finding <math>r</math>. Let <math>a</math> be the length of the tangent segment from <math>A</math> to <math>\omega</math>, and analogously define <math>b</math>, <math>c</math>, <math>d</math>, and <math>e</math>. Then <math>a+b=5</math>, <math>b+c= c+d=d+e=6</math>, and <math>e+a=7</math>, with a total of <math>a+b+c+d+e=15</math>. Hence <math>a=3</math>, <math>b=d=2</math>, and <math>c=e=4</math>. It follows that <math>\angle B= \angle D</math> and <math>\angle C= \angle E</math>. Let <math>Q</math> be the point where <math>\omega</math> is tangent to <math>\overline{CD}</math>. Then <math>\angle IAE = \angle IAB =\frac{1}{2}\angle A</math>. Now we claim that points <math>A, I, Q</math> are collinear, which can be proved if <math>\angle{AIQ}=\angle{QIA}=180^{\circ}</math>. The sum of the internal angles in polygons <math>ABCQI</math> and <math>AIQDE</math> are equal, so <math>\angle IAE + \angle AIQ + \angle IQD + \angle D + \angle E = \angle IAB + \angle B + \angle C + \angle CQI + \angle QIA</math>, which implies that <math>\angle AIQ</math> must be <math>180^\circ</math>. Therefore points <math>A</math>, <math>I</math>, and <math>Q</math> are collinear.
 <asy>
 defaultpen(fontsize(8pt));
@@ Line 68: / Line 88: @@
 <cmath>\cos (\angle B) =\frac{1-\tan^2 \left(\frac{\angle B}{2}\right)}{1+\tan^2 \left(\frac{\angle B}{2}\right)} =  \frac{4-r^2}{4+r^2}</cmath>and
 <cmath>\cos (\angle E) = \frac{1-\tan^2 \left(\frac{\angle E}{2}\right)}{1+\tan^2 \left(\frac{\angle E}{2}\right)}= \frac{16-r^2}{16+r^2}.</cmath>Applying the Law of Cosines to <math>\triangle ABC</math> and <math>\triangle AED</math> gives
-\[
+<cmath>AC^2=AB^2+BC^2-2\cdot AB\cdot BC\cdot \cos (\angle B) = 5^2+6^2-2 \cdot 5 \cdot 6 \cdot \frac{4-r^2}{4+r^2}</cmath>
-AC^2=AB^2+BC^2-2\cdot AB\cdot BC\cdot \cos (\angle B) = 5^2+6^2-2 \cdot 5 \cdot 6 \cdot \frac{4-r^2}{4+r^2}
+and
-\]and
+<cmath>AD^2=AE^2+DE^2-2 \cdot AE \cdot DE \cdot \cos(\angle E) = 7^2+6^2-2 \cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2}.</cmath>
-\[
+Hence
-AD^2=AE^2+DE^2-2 \cdot AE \cdot DE \cdot \cos(\angle E) = 7^2+6^2-2 \cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2}.
-\]Hence
+<cmath>12=AC^2- AD^2= 5^2-2\cdot 5 \cdot 6\cdot \frac{4-r^2}{4+r^2} -7^2+2\cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2},</cmath>
-\[
+yielding
-=AC^2- AD^2= 5^2-2\cdot 5 \cdot 6\cdot \frac{4-r^2}{4+r^2} -7^2+2\cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2},
+<cmath>2\cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2}- 2\cdot 5 \cdot 6\cdot \frac{4-r^2}{4+r^2}= 36;</cmath>
-\]yielding
+equivalently
-\[
+<cmath>7(16-r^2)(4+r^2)-5(4-r^2)(16+r^2) = 3(16+r^2)(4+r^2).</cmath>
-\cdot 7 \cdot 6 \cdot \frac{16-r^2}{16+r^2}- 2\cdot 5 \cdot 6\cdot \frac{4-r^2}{4+r^2}= 36;
+Substituting <math>x=r^2</math> gives the quadratic equation <math>5x^2-84x+64=0</math>, with solutions <math>\frac{42 - 38}{5}=\frac45</math>, and <math>\frac{42 + 38}{5}= 16</math>. The solution <math>r^2=\frac45</math> corresponds to a five-pointed star, which is not convex. Indeed, if <math>r<3</math>, then <math> \tan \left(\frac{\angle A}{2}\right)</math>, <math>\tan \left(\frac{\angle C}{2}\right)</math>, and <math>\tan \left(\frac{\angle E}{2}\right)</math> are less than <math>1,</math> implying that <math>\angle A</math>, <math>\angle C</math>, and <math>\angle E</math> are acute, which cannot happen in a convex pentagon. Thus <math>r^2=16</math> and <math>r=4</math>. The requested area is <math>15\cdot4 = \boxed{60}</math>.
-\]equivalently
-\[
+==Solution 6 (Official MAA 2)==
-(16-r^2)(4+r^2)-5(4-r^2)(16+r^2) = 3(16+r^2)(4+r^2).
+Define <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math>, <math>e</math>, and <math>r</math> as in Solution 5. Then, as in Solution 5, <math>a=3</math>, <math>b=d=2</math>, <math>c=e=4</math>, <math>\angle B= \angle D</math>, and <math>\angle C= \angle E</math>. Let <math>\alpha =\frac{\angle A}{2}</math>, <math>\beta = \frac{\angle B}{2}</math>, and <math>\gamma=\frac{\angle C}{2}</math>. It follows that <math>540^{\circ} = 2\alpha + 4 \beta + 4 \gamma</math>, so <math>270^{\circ} = \alpha + 2\beta + 2 \gamma</math>. Thus
-\]
+<cmath>\tan(2\beta + 2 \gamma) = \frac{1}{\tan \alpha},</cmath>
-Substituting <math>x=r^2</math> gives the quadratic equation <math>5x^2-84x+64=0</math>, with solutions <math>\frac{42 - 38}{5}=\frac45</math>, and <math>\frac{42 + 38}{5}= 16</math>. The solution <math>r^2=\frac45</math> corresponds to a five-pointed star, which is not convex. Indeed, if <math>r<3</math>, then <math> \tan \left(\frac{\angle A}{2}\right)</math>, <math>\tan \left(\frac{\angle C}{2}\right)</math>, and <math>\tan \left(\frac{\angle E}{2}\right)</math> are less than <math>1,</math> implying that <math>\angle A</math>, <math>\angle C</math>, and <math>\angle E</math> are acute, which cannot happen in a convex pentagon. Thus <math>r^2=16</math> and <math>r=4</math>. The requested area is <math>15\cdot4 = 60</math>.
+<math>\tan(\beta) = \frac{r}{2}</math>, <math>\tan(\gamma) = \frac{r}{4}</math>, and <math>\tan(\alpha) = \frac {r}{3}</math>. By the Tangent Addition Formula,
+<cmath>\tan(\beta +\gamma) = \frac{6r}{8-r^2}</cmath>
+and
+<cmath>\tan(2\beta + 2\gamma) = \frac{\frac{12r}{8-r^2}}{1-\frac{36r^2}{(8-r^2)^2}} = \frac{12r(8-r^2)}{(8-r^2)^2-36r^2}.</cmath>
+Therefore
+<cmath>\frac{12r(8-r^2)}{(8-r^2)^2-36r^2} = \frac{3}{r},</cmath>
+which simplifies to <math>5r^4 - 84r^2 + 64 = 0</math>. Then the solution proceeds as in Solution 5.
+==Solution 7 (Official MAA 3)==
+Define <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math>, <math>e</math>, and <math>r</math> as in Solution 5. Note that
+<cmath>\arctan\left(\frac{a}{r}\right) + \arctan\left(\frac{b}{r}\right) + \arctan\left(\frac{c}{r}\right) + \arctan\left(\frac{d}{r}\right) + \arctan\left(\frac{e}{r}\right) = 180^{\circ}.</cmath>
+Hence
+<cmath>\operatorname{Arg}(r + 3i) + 2\cdot \operatorname{Arg}(r + 2i) + 2\cdot  \operatorname{Arg}(r + 4i) = 180^{\circ}.</cmath>
+Therefore
+<cmath>\operatorname{Im} \big( (r + 3i)(r+2i)^2(r+4i)^2 \big) = 0.</cmath>
+Simplifying this equation gives the same quadratic equation in <math>r^2</math> as in Solution 5.
+==Solution 8 (The same circle)==
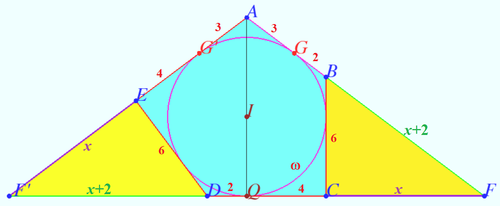
+[[File:2020 AIME II 13.png|500px|right]]
+Notation shown on diagram. As in solution 5, we get  <math>\overline{AQ} \perp  \overline{CD}, AG = 3, GB = 2, CQ = 4</math> and so on.
+Let <math> \overline{AB}</math> cross <math> \overline{CD}</math> at <math>F,  \overline{AE}</math> cross <math> \overline{CD}</math> at <math>F', CF = x.</math>
+<math>FQ = FG \implies FB = x+2.</math>
+<math>\angle BAQ = \angle EAQ \implies DF' = x + 2, EF' = x.</math>
+Triangle <math>\triangle AFF'</math> has semiperimeter <math>s = 2x + 11.</math>
+The radius of <i><b>incircle</b></i> <math>\omega</math> is
+<math>r =\sqrt{\frac{s-FF’}{s}}(s-AF) = \sqrt{\frac{3}{2x +11}}(x+4). </math>
+Triangle <math>\triangle BCF</math> has semiperimeter <math>s = x + 4.</math>
+The radius of <i><b>excircle </b></i> <math>\omega</math> is
+<math>r = \sqrt{\frac{s(s-BF)(s-CF)}{s-BC}} = \sqrt{ \frac{(x+4)\cdot 2 \cdot 4}{x - 2}}.</math>
+It is the same radius, therefore
+<cmath> \sqrt{\frac{3}{2x +11}}(x+4) = \sqrt{\frac{8(x+4)}{x – 2}} \implies \frac {3(x+4)}{2x+11} = \frac {8}{x-2} \implies (x-8)(3x + 14) = 0 \implies x = 8, r = 4.</cmath>
-==Video Solution==
+Then the solution proceeds as in Solution 5.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Video Solution 1 by MOP 2024==
+https://youtube.com/watch?v=BXEXcCNXrlM
+~r00tsOfUnity
+==Video Solution 2==
 https://youtu.be/bz5N-jI2e0U?t=327
+==Video Solution 3==
+https://youtu.be/_fwkGTdMd8U
+==Video Solution 4==
+https://youtu.be/kn3c2LStiHA
+(solve in 5 minutes)
+~MathProblemSolvingSkills.com
 {{AIME box|year=2020|n=II|num-b=12|num-a=14}}
+[[Category: Intermediate Geometry Problems]]
 {{MAA Notice}}

Page

Toolbox

Search