Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2018 IMO Problems/Problem 6"

(→‎Solution)
 
(12 intermediate revisions by one other user not shown)
Line 1: Line 1:
 +
==Problem==
 +
 
A convex quadrilateral <math>ABCD</math> satisfies <math>AB\cdot CD=BC \cdot DA.</math> Point <math>X</math> lies inside
 
A convex quadrilateral <math>ABCD</math> satisfies <math>AB\cdot CD=BC \cdot DA.</math> Point <math>X</math> lies inside
 
<math>ABCD</math> so that
 
<math>ABCD</math> so that
Line 5: Line 7:
  
 
==Solution==
 
==Solution==
−
[[File:2018 IMO 6.png|490px|right]]
+
[[File:2018 IMO 6bb.png|470px|right]]
−
Suppose point X is unique. We will construct point <math>X_0</math> and prove that <math>X_0</math> coincides with the point <math>X.</math>
+
[[File:2018 IMO 6.png|470px|right]]
 +
[[File:2018 IMO 6e.png|470px|right]]
 +
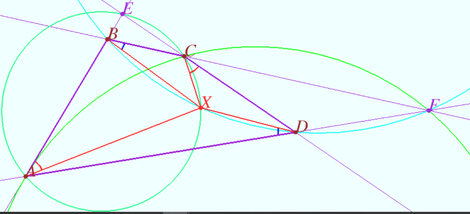
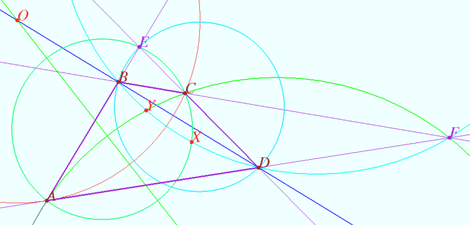
We want to find the point <math>X.</math> Let <math>E</math> and <math>F</math> be the intersection points of <math>AB</math> and <math>CD,</math> and <math>BC</math> and <math>DA,</math> respectively.
 +
The poinx <math>X</math> is inside <math>ABCD,</math> so points <math>E,A,X,C</math> follow in this order.
  
−
<i><b>Special case</b></i>
+
<math>\angle XAB =  \angle XCD \implies  \angle XAE +  \angle XCE = 180^\circ </math>
 +
<math>\implies AXCE</math> is cyclic <math>\implies X</math> lie on circle <math>ACE.</math>
  
−
Let <math>AD = CD</math> and <math>AB = BC \implies  AB \cdot CD = BC \cdot DA.</math>
+
Similarly, <math>X</math> lie on circle <math>BDF.</math>
  
−
Let <math>E</math> and <math>F</math> be the intersection points of <math>AB</math> and <math>CD,</math> and <math>BC</math> and <math>DA,</math> respectively.
+
Point <math>X</math> is the point of intersection of circles  <math>ACE</math> and <math>\Omega = BDF.</math>
  
−
The points <math>B</math> and <math>D</math> are symmetric with respect to the circle <math>\omega = ACEF</math> <i><b>(Claim 1).</b></i>
+
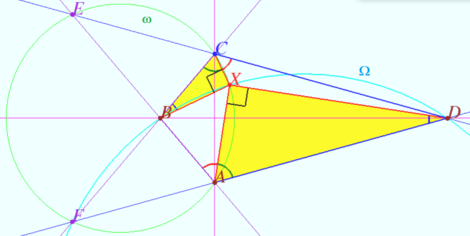
<i><b>Special case</b></i>
  
−
The circle <math>\Omega = FBD</math> is orthogonal to the circle <math>\omega</math> <i><b>(Claim 2).</b></i>
+
Let <math>AD = CD</math> and <math>AB = BC \implies  AB \cdot CD = BC \cdot DA.</math>
  
−
Let <math>X_0</math> be the point of intersection of the circles <math>\omega</math> and <math>\Omega.</math>
+
The points <math>B</math> and <math>D</math> are symmetric with respect to the circle <math>\theta = ACEF</math> <i><b>(Claim 1).</b></i>
−
Quadrilateral <math>AX_0CF</math> is cyclic <math>\implies</math> <cmath>\angle X_0AB = \frac {\overset{\Large\frown} {X_0CE}}{2}  =  \frac {360^\circ -\overset{\Large\frown} {X_0AFE}}{2} = 180^\circ  - \angle X_0CE = \angle X_0CD.</cmath>
 
  
−
Similarly, quadrangle <math>DX_0BF</math> is cyclic <math>\implies \angle X_0BC = \angle X_0DA</math>. This means that point <math>X_0</math> coincides with the point <math>X</math>.
+
The circle <math>BDF</math> is orthogonal to the circle <math>\theta</math> <i><b>(Claim 2).</b></i>
  
−
<math>\hspace{10mm} \angle FCX =  \angle BCX  =  \frac {\overset{\Large\frown} {XAF}}{2}</math> of <math>\omega.</math> <math>\hspace{10mm} \angle CBX = \angle XDA =  \frac {\overset{\Large\frown} {XBF}}{2}</math> of <math>\Omega.</math>
+
<math>\hspace{10mm} \angle FCX =  \angle BCX  =  \frac {\overset{\Large\frown} {XAF}}{2}</math> of <math>\theta.</math> <math>\hspace{10mm} \angle CBX = \angle XDA =  \frac {\overset{\Large\frown} {XBF}}{2}</math> of <math>\Omega.</math>
  
−
The sum <math>\overset{\Large\frown} {XAF} + \overset{\Large\frown} {XBF} = 180^\circ</math>  <i><b>(Claim 3)</b></i> <math>\implies</math>  
+
<math>\overset{\Large\frown} {XAF} + \overset{\Large\frown} {XBF} = 180^\circ</math>  <i><b>(Claim 3)</b></i> <math>\implies</math>  
 
<math>\angle XCB + \angle XBC = 90^\circ \implies \angle CXB = 90^\circ.</math>
 
<math>\angle XCB + \angle XBC = 90^\circ \implies \angle CXB = 90^\circ.</math>
  
−
Similarly, <math>\angle AXD =  90^\circ \implies \angle BXA + \angle DXC = 360^\circ -\angle AXD -\angle CXB = 180^\circ.</math>
+
Similarly, <math>\angle AXD =  90^\circ \implies</math>
 +
<cmath>\angle BXA + \angle DXC = 360^\circ -\angle AXD -\angle CXB = 180^\circ.</cmath>
  
−
[[File:2018 IMO 6a.png|430px|right]]
+
[[File:2018 IMO 6c.png|470px|right]]
−
[[File:2018 IMO 6bb.png|430px|right]]
+
[[File:2018 IMO 6d.png|470px|right]]
−
[[File:2018 IMO 6c.png|430px|right]]
 
−
[[File:2018 IMO 6d.png|430px|right]]
 
  
 
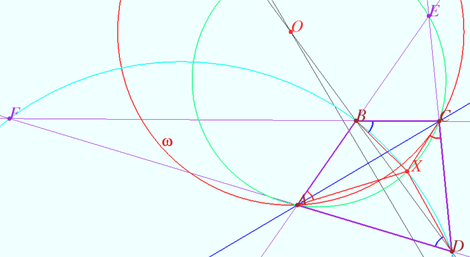
<i><b>Common case </b></i>
 
<i><b>Common case </b></i>
  
−
Denote by <math>O</math> the intersection point of <math>BD</math> and the perpendicular bisector of <math>AC.</math> Let <math>\omega</math> be a circle (red) with center <math>O</math> and radius <math>OA.</math>
+
Denote by <math>O</math> the intersection point of <math>BD</math> and the perpendicular bisector of <math>AC.</math> Let <math>\omega</math> be a circle (red) with center <math>O</math> and radius <math>OA = R.</math>
  
−
The points <math>B</math> and <math>D</math> are symmetric with respect to the circle <math>\omega</math> <i><b>(Claim 1).</b></i>
+
We will prove <math>\sin\angle BXA =\sin \angle DXC</math> using point <math>Y</math> symmetric to <math>X</math> with respect to <math>\omega.</math>
 +
 
 +
The points <math>B</math> and <math>D</math> are symmetric with respect to <math>\omega</math> <i><b>(Claim 1).</b></i>
  
 
The circles <math>BDF</math> and <math>BDE</math> are orthogonal to the circle <math>\omega</math> <i><b>(Claim 2).</b></i>
 
The circles <math>BDF</math> and <math>BDE</math> are orthogonal to the circle <math>\omega</math> <i><b>(Claim 2).</b></i>
  
 
Circles <math>ACF</math> and <math>ACE</math> are symmetric with respect to the circle <math>\omega</math> <i><b>(Lemma).</b></i>
 
Circles <math>ACF</math> and <math>ACE</math> are symmetric with respect to the circle <math>\omega</math> <i><b>(Lemma).</b></i>
−
 
−
Denote by <math>X_0</math> the point of intersection of the circles <math>BDF</math> and <math>ACE.</math>
 
−
Quadrangle <math>BX_0DF</math> is cyclic <math>\implies \angle X_0BC =  \angle X_0DA</math> (see Special case).
 
−
Similarly, quadrangle <math>AX_0CE</math> is cyclic <math>\implies \angle X_0AB =  \angle X_0CD.</math>
 
−
 
−
This means that point <math>X_0</math> coincides with the point <math>X</math>.
 
  
 
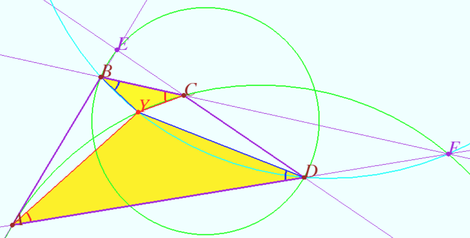
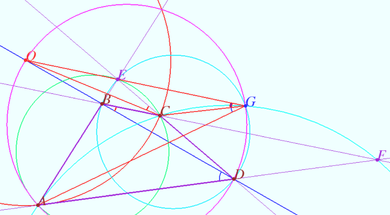
Denote by <math>Y</math> the point of intersection of circles <math>BDF</math> and <math>ACF.</math>
 
Denote by <math>Y</math> the point of intersection of circles <math>BDF</math> and <math>ACF.</math>
Line 55: Line 55:
 
Quadrangle <math>BYDF</math> is cyclic <math>\implies  \angle CBY =  \angle ADY.</math>
 
Quadrangle <math>BYDF</math> is cyclic <math>\implies  \angle CBY =  \angle ADY.</math>
  
−
Quadrangle <math>AYCF</math> is cyclic <math>\implies  \angle YAD = \angle BCY.</math>  
+
Quadrangle <math>AYCF</math> is cyclic <math>\implies  \angle YAD = \angle YCB.</math>  
  
 
The triangles <math>\triangle YAD \sim \triangle YCB</math> by two angles, so <cmath>\frac {BC}{AD} = \frac {CY}{AY} = \frac {BY} {DY} \hspace{10mm} (1).</cmath>
 
The triangles <math>\triangle YAD \sim \triangle YCB</math> by two angles, so <cmath>\frac {BC}{AD} = \frac {CY}{AY} = \frac {BY} {DY} \hspace{10mm} (1).</cmath>
Line 61: Line 61:
 
The points <math>X</math> and <math>Y</math> are symmetric with respect to the circle <math>\omega</math>, since they lie on the intersection of the circles <math>ACF</math> and <math>ACE</math> symmetric with respect to <math>\omega</math> and the  circle <math>BDF</math> orthogonal to <math>\omega.</math>
 
The points <math>X</math> and <math>Y</math> are symmetric with respect to the circle <math>\omega</math>, since they lie on the intersection of the circles <math>ACF</math> and <math>ACE</math> symmetric with respect to <math>\omega</math> and the  circle <math>BDF</math> orthogonal to <math>\omega.</math>
  
−
The point <math>C</math> is symmetric to itself, the point <math>X</math> is symmetric to <math>Y</math> with respect to <math>\omega \implies \frac{CX}{CY} = \frac {R^2}{OC \cdot OY} , \frac {AX}{AY} = \frac {R^2}{OA \cdot OY}.</math>
+
The point <math>B</math> is symmetric to <math>D</math> with respect to <math>\omega \implies</math>
−
Usung <math>(1)</math> and the equality <math>OA = OC,</math> we get <cmath>\frac{CY}{AY} = \frac {CX}{AX} = \frac{BC}{AD}.</cmath>
 
−
The point <math>C</math> is symmetric to itself, the point <math>B</math> is symmetric to <math>D</math> with respect to <math>\omega \implies</math>
 
 
<cmath>\triangle OBC \sim \triangle OCD \implies \frac {OB}{OC} = \frac {BC}{CD} = \frac {OC}{OD},</cmath>
 
<cmath>\triangle OBC \sim \triangle OCD \implies \frac {OB}{OC} = \frac {BC}{CD} = \frac {OC}{OD},</cmath>
 
<cmath>\frac {OB}{OD} = \frac {OB}{OC} \cdot \frac {OC}{OD} = \frac{BC^2}{CD^2} = \frac{BC}{CD} \cdot \frac {AB}{AD}.</cmath>
 
<cmath>\frac {OB}{OD} = \frac {OB}{OC} \cdot \frac {OC}{OD} = \frac{BC^2}{CD^2} = \frac{BC}{CD} \cdot \frac {AB}{AD}.</cmath>
Line 69: Line 67:
 
<cmath>\frac {BX}{DY} = \frac {R^2}{OD \cdot OY} ,\frac {DX}{BY} = \frac{R^2}{OB \cdot OY}.</cmath>
 
<cmath>\frac {BX}{DY} = \frac {R^2}{OD \cdot OY} ,\frac {DX}{BY} = \frac{R^2}{OB \cdot OY}.</cmath>
 
<cmath>\frac{BX}{DX} =\frac{DY}{BY} \cdot \frac {OB}{OD} = \frac{AD}{BC} \cdot \frac{BC}{CD} \cdot \frac{AB}{AD} = \frac{AB}{CD}.</cmath>
 
<cmath>\frac{BX}{DX} =\frac{DY}{BY} \cdot \frac {OB}{OD} = \frac{AD}{BC} \cdot \frac{BC}{CD} \cdot \frac{AB}{AD} = \frac{AB}{CD}.</cmath>
−
[[File:2018 IMO 6 angles.png|350px|right]]
+
[[File:2018 IMO 6 angles.png|390px|right]]
 +
[[File:2018 IMO 6 Claim 3.png|390px|right]]
 +
[[File:2018 IMO 6a.png|390px|right]]
 +
 
 
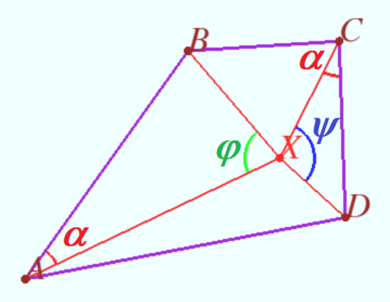
Denote  <math>\angle XAB =  \angle XCD = \alpha,  \angle BXA = \varphi,  \angle DXC = \psi.</math>
 
Denote  <math>\angle XAB =  \angle XCD = \alpha,  \angle BXA = \varphi,  \angle DXC = \psi.</math>
 
   
 
   
Line 81: Line 82:
 
<math>CD \cdot BC = AB \cdot AD \implies AD = CD, AB = BC.</math> This is a special case.  
 
<math>CD \cdot BC = AB \cdot AD \implies AD = CD, AB = BC.</math> This is a special case.  
  
−
In all other cases, the equality of the sines follows <math>\psi = 180° – \varphi \implies \varphi + \psi = 180°.</math>
+
In all other cases, the equality of the sines follows <math>\varphi + \psi = 180^\circ .</math>
  
 
<i><b>Claim 1</b></i> Let <math>A, C,</math> and <math>E</math> be arbitrary points on a circle <math>\omega, l</math> be the perpendicular bisector to the segment <math>AC.</math> Then the straight lines <math>AE</math> and <math>CE</math> intersect <math>l</math> at the points <math>B</math> and <math>D,</math> symmetric with respect to <math>\omega.</math>
 
<i><b>Claim 1</b></i> Let <math>A, C,</math> and <math>E</math> be arbitrary points on a circle <math>\omega, l</math> be the perpendicular bisector to the segment <math>AC.</math> Then the straight lines <math>AE</math> and <math>CE</math> intersect <math>l</math> at the points <math>B</math> and <math>D,</math> symmetric with respect to <math>\omega.</math>
  
−
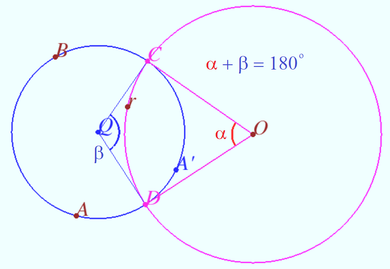
[[File:2018 IMO 6 Claim 3.png|370px|right]]
 
−
[[File:2018 IMO 6a.png|430px|right]]
 
 
<i><b>Claim 2</b></i> Let points <math>B</math> and <math>D</math> be symmetric with respect to the circle <math>\omega.</math> Then any circle <math>\Omega</math> passing through these points is orthogonal to <math>\omega.</math>
 
<i><b>Claim 2</b></i> Let points <math>B</math> and <math>D</math> be symmetric with respect to the circle <math>\omega.</math> Then any circle <math>\Omega</math> passing through these points is orthogonal to <math>\omega.</math>
  
Line 94: Line 93:
 
<i><b>Lemma</b></i> The opposite sides of the quadrilateral <math>ABCD</math> intersect at points <math>E</math> and <math>F</math> (<math>E</math> lies on <math>AB</math>). The circle  <math>\omega</math> centered at the point <math>O</math> contains the ends of the diagonal <math>AC.</math> The points <math>B</math> and <math>D</math> are symmetric with respect to the circle <math>\omega</math> (in other words, the inversion with respect to <math>\omega</math> maps <math>B</math> into <math>D).</math> Then the circles <math>ACE</math> and <math>ACF</math> are symmetric with respect to <math>\omega.</math>
 
<i><b>Lemma</b></i> The opposite sides of the quadrilateral <math>ABCD</math> intersect at points <math>E</math> and <math>F</math> (<math>E</math> lies on <math>AB</math>). The circle  <math>\omega</math> centered at the point <math>O</math> contains the ends of the diagonal <math>AC.</math> The points <math>B</math> and <math>D</math> are symmetric with respect to the circle <math>\omega</math> (in other words, the inversion with respect to <math>\omega</math> maps <math>B</math> into <math>D).</math> Then the circles <math>ACE</math> and <math>ACF</math> are symmetric with respect to <math>\omega.</math>
  
−
<i><b>Proof</b></i>  We will prove that the point <math>G,</math> symmetric to the point <math>E</math> with respect to <math>\omega,</math> belongs to the circle <math>ACF.</math> For this, we will prove the equality <math>\angle AGC = \angle AFC.</math>
+
<i><b>Proof</b></i>  We will prove that the point <math>G,</math> symmetric to the point <math>E</math> with respect to <math>\omega,</math> belongs to the circle <math>ACF</math> becouse <math>\angle AGC = \angle AFC.</math>
  
−
A circle <math>BDE</math> containing points <math>B</math> and <math>D</math> symmetric with respect to <math>\omega,</math> is orthogonal to <math>\omega</math> (Claim 2) and maps into itself under inversion with respect to the circle <math>\omega.</math> Hence, the point <math>E</math> under this inversion passes to some point <math>G,</math> of the same circle <math>BDE.</math>
+
A circle <math>BDE</math> containing points <math>B</math> and <math>D</math> symmetric with respect to <math>\omega,</math> is orthogonal to <math>\omega</math> <i><b>(Claim 2)</b></i> and maps into itself under inversion with respect to the circle <math>\omega.</math> Hence, the point <math>E</math> under this inversion passes to some point <math>G,</math> of the same circle <math>BDE.</math>
  
 
A straight line <math>ABE</math> containing the point <math>A</math> of the circle <math>\omega,</math> under inversion with respect to <math>\omega,</math> maps into the circle <math>OADG.</math> Hence, the inscribed angles of this circle are equal  <math>\angle ADB =  \angle AGE.</math>
 
A straight line <math>ABE</math> containing the point <math>A</math> of the circle <math>\omega,</math> under inversion with respect to <math>\omega,</math> maps into the circle <math>OADG.</math> Hence, the inscribed angles of this circle are equal  <math>\angle ADB =  \angle AGE.</math>
Line 102: Line 101:
 
Consequently, the angles  <math>\angle AFC =  \angle ADB –  \angle FBD = \angle AGE -  \angle CGE =  \angle AGC.</math>
 
Consequently, the angles  <math>\angle AFC =  \angle ADB –  \angle FBD = \angle AGE -  \angle CGE =  \angle AGC.</math>
 
These angles subtend the <math>\overset{\Large\frown} {AC}</math> of the <math>ACF</math> circle, that is, the point <math>G,</math> symmetric to the point <math>E</math> with respect to <math>\omega,</math> belongs to the circle <math>ACF.</math>
 
These angles subtend the <math>\overset{\Large\frown} {AC}</math> of the <math>ACF</math> circle, that is, the point <math>G,</math> symmetric to the point <math>E</math> with respect to <math>\omega,</math> belongs to the circle <math>ACF.</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
 +
==See Also==
 +
 +
{{IMO box|year=2018|num-b=5|after=Last Problem}}

Latest revision as of 00:47, 19 November 2023

Problem

A convex quadrilateral $ABCD$ satisfies $AB\cdot CD=BC \cdot DA.$ Point $X$ lies inside $ABCD$ so that $\angle XAB = \angle XCD$ and $\angle XBC = \angle XDA.$ Prove that $\angle BXA + \angle DXC = 180^{\circ}$

Solution

2018 IMO 6bb.png
2018 IMO 6.png
2018 IMO 6e.png

We want to find the point $X.$ Let $E$ and $F$ be the intersection points of $AB$ and $CD,$ and $BC$ and $DA,$ respectively. The poinx $X$ is inside $ABCD,$ so points $E,A,X,C$ follow in this order.

$\angle XAB = \angle XCD \implies \angle XAE + \angle XCE = 180^\circ$ $\implies AXCE$ is cyclic $\implies X$ lie on circle $ACE.$

Similarly, $X$ lie on circle $BDF.$

Point $X$ is the point of intersection of circles $ACE$ and $\Omega = BDF.$

Special case

Let $AD = CD$ and $AB = BC \implies AB \cdot CD = BC \cdot DA.$

The points $B$ and $D$ are symmetric with respect to the circle $\theta = ACEF$ (Claim 1).

The circle $BDF$ is orthogonal to the circle $\theta$ (Claim 2).

$\hspace{10mm} \angle FCX = \angle BCX = \frac {\overset{\Large\frown} {XAF}}{2}$ of $\theta.$ $\hspace{10mm} \angle CBX = \angle XDA = \frac {\overset{\Large\frown} {XBF}}{2}$ of $\Omega.$

$\overset{\Large\frown} {XAF} + \overset{\Large\frown} {XBF} = 180^\circ$ (Claim 3) $\implies$ $\angle XCB + \angle XBC = 90^\circ \implies \angle CXB = 90^\circ.$

Similarly, $\angle AXD = 90^\circ \implies$ \[\angle BXA + \angle DXC = 360^\circ -\angle AXD -\angle CXB = 180^\circ.\]

2018 IMO 6c.png
2018 IMO 6d.png

Common case

Denote by $O$ the intersection point of $BD$ and the perpendicular bisector of $AC.$ Let $\omega$ be a circle (red) with center $O$ and radius $OA = R.$

We will prove $\sin\angle BXA =\sin \angle DXC$ using point $Y$ symmetric to $X$ with respect to $\omega.$

The points $B$ and $D$ are symmetric with respect to $\omega$ (Claim 1).

The circles $BDF$ and $BDE$ are orthogonal to the circle $\omega$ (Claim 2).

Circles $ACF$ and $ACE$ are symmetric with respect to the circle $\omega$ (Lemma).

Denote by $Y$ the point of intersection of circles $BDF$ and $ACF.$

Quadrangle $BYDF$ is cyclic $\implies \angle CBY = \angle ADY.$

Quadrangle $AYCF$ is cyclic $\implies \angle YAD = \angle YCB.$

The triangles $\triangle YAD \sim \triangle YCB$ by two angles, so \[\frac {BC}{AD} = \frac {CY}{AY} = \frac {BY} {DY} \hspace{10mm} (1).\]

The points $X$ and $Y$ are symmetric with respect to the circle $\omega$, since they lie on the intersection of the circles $ACF$ and $ACE$ symmetric with respect to $\omega$ and the circle $BDF$ orthogonal to $\omega.$

The point $B$ is symmetric to $D$ with respect to $\omega \implies$ \[\triangle OBC \sim \triangle OCD \implies \frac {OB}{OC} = \frac {BC}{CD} = \frac {OC}{OD},\] \[\frac {OB}{OD} = \frac {OB}{OC} \cdot \frac {OC}{OD} = \frac{BC^2}{CD^2} = \frac{BC}{CD} \cdot \frac {AB}{AD}.\] The point $B$ is symmetric to $D$ and the point $X$ is symmetric to $Y$ with respect to $\omega,$ hence \[\frac {BX}{DY} = \frac {R^2}{OD \cdot OY} ,\frac {DX}{BY} = \frac{R^2}{OB \cdot OY}.\] \[\frac{BX}{DX} =\frac{DY}{BY} \cdot \frac {OB}{OD} = \frac{AD}{BC} \cdot \frac{BC}{CD} \cdot \frac{AB}{AD} = \frac{AB}{CD}.\]

2018 IMO 6 angles.png
2018 IMO 6 Claim 3.png
2018 IMO 6a.png

Denote $\angle XAB = \angle XCD = \alpha, \angle BXA = \varphi, \angle DXC = \psi.$

By the law of sines for $\triangle ABX,$ we obtain $\frac {AB}{\sin \varphi} = \frac{BX}{\sin \alpha}.$

By the law of sines for $\triangle CDX,$ we obtain $\frac {CD}{\sin \psi} = \frac {DX}{\sin \alpha}.$

Hence we get $\frac{\sin \psi} {\sin \varphi}= \frac {CD}{DX} \cdot \frac{BX}{AB} = 1.$

If $\varphi = \psi,$ then $\triangle XAB \sim \triangle XCD \implies \frac {CD}{AB} = \frac {BX}{DX} = \frac{AX}{CX} = \frac {AD}{BC}.$ $CD \cdot BC = AB \cdot AD \implies AD = CD, AB = BC.$ This is a special case.

In all other cases, the equality of the sines follows $\varphi + \psi = 180^\circ .$

Claim 1 Let $A, C,$ and $E$ be arbitrary points on a circle $\omega, l$ be the perpendicular bisector to the segment $AC.$ Then the straight lines $AE$ and $CE$ intersect $l$ at the points $B$ and $D,$ symmetric with respect to $\omega.$

Claim 2 Let points $B$ and $D$ be symmetric with respect to the circle $\omega.$ Then any circle $\Omega$ passing through these points is orthogonal to $\omega.$

Claim 3 The sum of the arcs between the points of intersection of two perpendicular circles is $180^\circ.$ In the figure they are a blue and red arcs $\overset{\Large\frown} {CD}, \alpha + \beta = 180^\circ.$

Lemma The opposite sides of the quadrilateral $ABCD$ intersect at points $E$ and $F$ ($E$ lies on $AB$). The circle $\omega$ centered at the point $O$ contains the ends of the diagonal $AC.$ The points $B$ and $D$ are symmetric with respect to the circle $\omega$ (in other words, the inversion with respect to $\omega$ maps $B$ into $D).$ Then the circles $ACE$ and $ACF$ are symmetric with respect to $\omega.$

Proof We will prove that the point $G,$ symmetric to the point $E$ with respect to $\omega,$ belongs to the circle $ACF$ becouse $\angle AGC = \angle AFC.$

A circle $BDE$ containing points $B$ and $D$ symmetric with respect to $\omega,$ is orthogonal to $\omega$ (Claim 2) and maps into itself under inversion with respect to the circle $\omega.$ Hence, the point $E$ under this inversion passes to some point $G,$ of the same circle $BDE.$

A straight line $ABE$ containing the point $A$ of the circle $\omega,$ under inversion with respect to $\omega,$ maps into the circle $OADG.$ Hence, the inscribed angles of this circle are equal $\angle ADB = \angle AGE.$ $\angle OCE = \angle CGE (CE$ maps into $CG)$ and $\angle OCE = \angle BCD (BC$ maps into $DC).$ Consequently, the angles $\angle AFC = \angle ADB – \angle FBD = \angle AGE - \angle CGE = \angle AGC.$ These angles subtend the $\overset{\Large\frown} {AC}$ of the $ACF$ circle, that is, the point $G,$ symmetric to the point $E$ with respect to $\omega,$ belongs to the circle $ACF.$

vladimir.shelomovskii@gmail.com, vvsss


See Also

2018 IMO (Problems) • Resources
Preceded by
Problem 5 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Last Problem
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2018_IMO_Problems/Problem_6&oldid=204587"