Difference between revisions of "2023 AIME I Problems/Problem 13"
(Created page with "Each face of two noncongruent parallelepipeds is a rhombus whose diagonals have lengths <math>\sqrt{21}</math> and <math>\sqrt{31}</math>. The ratio of the volume of the large...") |
|||
| (18 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Problem== | ||
Each face of two noncongruent parallelepipeds is a rhombus whose diagonals have lengths <math>\sqrt{21}</math> and <math>\sqrt{31}</math>. | Each face of two noncongruent parallelepipeds is a rhombus whose diagonals have lengths <math>\sqrt{21}</math> and <math>\sqrt{31}</math>. | ||
The ratio of the volume of the larger of the two polyhedra to the volume of the smaller is <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> | The ratio of the volume of the larger of the two polyhedra to the volume of the smaller is <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> | ||
| Line 4: | Line 5: | ||
such as the one shown below. | such as the one shown below. | ||
| − | ==Solution (3- | + | <asy> |
| + | unitsize(2cm); | ||
| + | pair o = (0, 0), u = (1, 0), v = 0.8*dir(40), w = dir(70); | ||
| + | |||
| + | draw(o--u--(u+v)); | ||
| + | draw(o--v--(u+v), dotted); | ||
| + | draw(shift(w)*(o--u--(u+v)--v--cycle)); | ||
| + | draw(o--w); | ||
| + | draw(u--(u+w)); | ||
| + | draw(v--(v+w), dotted); | ||
| + | draw((u+v)--(u+v+w)); | ||
| + | </asy> | ||
| + | |||
| + | ==Solution 1 (3-D Vector Analysis)== | ||
Denote <math>\alpha = \tan^{-1} \frac{\sqrt{21}}{\sqrt{31}}</math>. | Denote <math>\alpha = \tan^{-1} \frac{\sqrt{21}}{\sqrt{31}}</math>. | ||
| Line 103: | Line 117: | ||
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ||
| + | |||
| + | ==Solution 2 (no trig)== | ||
| + | |||
| + | Let one of the vertices be at the origin and the three adjacent vertices be <math>u</math>, <math>v</math>, and <math>w</math>. For one of the parallelepipeds, the three diagonals involving the origin have length <math>\sqrt {21}</math>. Hence, <math>(u+v)\cdot (u+v)=u\cdot u+v\cdot v+2u\cdot v=21</math> and <math>(u-v)\cdot (u-v)=u\cdot u+v\cdot v-2u\cdot v=31</math>. Since all of <math>u</math>, <math>v</math>, and <math>w</math> have equal length, <math>u\cdot u=13</math>, <math>v\cdot v=13</math>, and <math>u\cdot v=-2.5</math>. Symmetrically, <math>w\cdot w=13</math>, <math>u\cdot w=-2.5</math>, and <math>v\cdot w=-2.5</math>. Hence the volume of the parallelepiped is given by <math>\sqrt{\operatorname{det}\begin{pmatrix}13&-2.5&-2.5\\-2.5&13&-2.5\\-2.5&-2.5&13\end{pmatrix}}=\sqrt{\operatorname{det}\begin{pmatrix}15.5&-15.5&0\\-2.5&13&-2.5\\0&-15.5&15.5\end{pmatrix}}=\sqrt{15.5^2\operatorname\det\begin{pmatrix}1&-1&0\\-2.5&13&-2.5\\0&-1&1\end{pmatrix}}=\sqrt{15.5^2\cdot 8}</math>. | ||
| + | |||
| + | For the other parallelepiped, the three diagonals involving the origin are of length <math>\sqrt{31}</math> and the volume is <math>\sqrt{\operatorname{det}\begin{pmatrix}13&2.5&2.5\\2.5&13&2.5\\2.5&2.5&13\end{pmatrix}}=\sqrt{\operatorname{det}\begin{pmatrix}10.5&-10.5&0\\2.5&13&2.5\\0&-10.5&10.5\end{pmatrix}}=\sqrt{10.5^2\operatorname\det\begin{pmatrix}1&-1&0\\2.5&13&2.5\\0&-1&1\end{pmatrix}}=\sqrt{10.5^2\cdot 18}</math>. | ||
| + | |||
| + | Consequently, the answer is <math>\sqrt\frac{10.5^2\cdot 18}{15.5^2\cdot 8}=\frac{63}{62}</math>, giving <math>\boxed{125}</math>. | ||
| + | |||
| + | ~EVIN- | ||
| + | |||
| + | ==Solution 3 (No trig, no linear algebra)== | ||
| + | |||
| + | Observe that both parallelepipeds have two vertices (one on each base) that have three congruent angles meeting at them. Denote the parallelepiped with three acute angles meeting <math>P</math>, and the one with three obtuse angles meeting <math>P'</math>. | ||
| + | |||
| + | The area of a parallelepiped is simply the base area times the height, but because both parallelepipeds have the same base, what we want is just the ratio of the heights. | ||
| + | |||
| + | Denote the point with three acute angles meeting at it in <math>P</math> as <math>A</math>, and its neighbors <math>B</math>, <math>C</math>, and <math>D</math>. Similarly, denote the point with three obtuse angles meeting at it in <math>P'</math> as <math>A'</math>, and its neighbors <math>B'</math>, <math>C'</math>, and <math>D'</math>. | ||
| + | |||
| + | We have the following equations: | ||
| + | |||
| + | <cmath>\textrm{Height of }P\textrm{ from }ACD = \frac{\textrm{Vol}(ABCD) \cdot 3}{[ACD]}, </cmath> | ||
| + | <cmath>\textrm{Height of }P'\textrm{ from }A'C'D' = \frac{\textrm{Vol}(A'B'C'D') \cdot 3}{[A'C'D']}.</cmath> | ||
| + | |||
| + | However, <math>ACD</math> and <math>A'C'D'</math> are both half the area of a rhombus with diagonals <math>\sqrt{31}</math> and <math>\sqrt{21}</math>, so our ratio is really | ||
| + | |||
| + | <cmath>\frac{P}{P'} = \frac{\textrm{Vol}(ABCD)}{\textrm{Vol}(A'B'C'D')}.</cmath> | ||
| + | |||
| + | Because the diagonals of all of the faces are <math>\sqrt{31}</math> and <math>\sqrt{21}</math>, each edge of the parallelepipeds is <math>\sqrt{13}</math> by the Pythagorean theorem. | ||
| + | |||
| + | We have <math>AB = AC = AD = \sqrt{13}</math>, and <math>BC = CD = BD = \sqrt{21}</math>. When we drop a perpendicular to the centroid of <math>BCD</math> from <math>A</math> (let's call this point <math>O</math>), we have <math>BO = \frac{\sqrt{21}}{\sqrt{3}} = \sqrt{7}</math>. Thus, | ||
| + | |||
| + | <cmath>AB^2 - BO^2 = AO^2</cmath> | ||
| + | <cmath>13 - 7 = AO^2 = 6</cmath> | ||
| + | <cmath>AO = \sqrt{6}.</cmath> | ||
| + | |||
| + | The area of base <math>BCD</math> is <math>\frac{21\sqrt{3}}{4}</math>. Hence, | ||
| + | |||
| + | <cmath>\textrm{Vol}(ABCD) = \frac{\sqrt{6}\cdot\frac{21\sqrt{3}}{4}}{3}</cmath> | ||
| + | <cmath> = \frac{63\sqrt{2}}{12}. </cmath> | ||
| + | |||
| + | We can apply a similar approach to <math>A'B'C'D'</math>. | ||
| + | |||
| + | <math>A'B' = A'C' = A'D' = \sqrt{13}</math>, and <math>B'C' = C'D' = B'D' = \sqrt{31}</math>. When we drop a perpendicular to the centroid of <math>B'C'D'</math> from <math>A'</math> (let's call this point <math>O'</math>), we have <math>B'O' = \frac{\sqrt{31}}{\sqrt{3}} = \sqrt{\frac{31}{3}}</math>. Thus, | ||
| + | |||
| + | <cmath>A'B'^2 - B'O'^2 = A'O'^2</cmath> | ||
| + | <cmath>13 - \frac{31}{3} = A'O'^2</cmath> | ||
| + | <cmath>A'O' = \sqrt{8}{3} = \frac{2\sqrt{6}}{3}.</cmath> | ||
| + | |||
| + | The area of base <math>B'C'D'</math> is <math>\frac{31\sqrt{3}}{4}</math>. Hence, | ||
| + | |||
| + | <cmath>\textrm{Vol}(A'B'C'D') = \frac{\frac{2\sqrt{6}}{3}\cdot\frac{31\sqrt{3}}{4}}{3}</cmath> | ||
| + | <cmath> = \frac{186\sqrt{2}}{36}</cmath> | ||
| + | <cmath> = \frac{62\sqrt{2}}{12}. </cmath> | ||
| + | |||
| + | Finally, | ||
| + | |||
| + | <cmath>\frac{P}{P'} = \frac{\textrm{Vol}(ABCD)}{\textrm{Vol}(A'B'C'D')} = \frac{\frac{63\sqrt{2}}{12}}{\frac{62\sqrt{2}}{12}} = \frac{63}{62}.</cmath> | ||
| + | |||
| + | Our answer is <math>63 + 62 = \boxed{125}</math>. | ||
| + | |||
| + | ~mathboy100 | ||
| + | |||
| + | ==Solution 4 (Pythagorean theorem)== | ||
| + | |||
| + | Since the two parallelepipeds have the same base, all we need to do is to find their respective heights. | ||
| + | |||
| + | <asy> | ||
| + | unitsize(2cm); | ||
| + | pair a = (0, 0), b = (1, 0), c = 0.8*dir(40), d = dir(70), p = 0.33*dir(20), o = (b+c)/2; | ||
| + | |||
| + | label("A",a,S); | ||
| + | label("B",b,S); | ||
| + | label("C",c,S); | ||
| + | label("D",d,N); | ||
| + | label("P",p,S); | ||
| + | label("O",o,E); | ||
| + | |||
| + | draw(a--b--(b+c)); | ||
| + | draw(a--c--(b+c), dotted); | ||
| + | draw(shift(d)*(a--b--(b+c)--c--cycle)); | ||
| + | draw(a--d); | ||
| + | draw(b--(b+d)); | ||
| + | draw(c--(c+d), dotted); | ||
| + | draw((b+c)--(b+c+d)); | ||
| + | |||
| + | draw(d--p, dotted); | ||
| + | draw(c--b, dotted); | ||
| + | draw(a--(b+c), dotted); | ||
| + | draw(p--c, dotted); | ||
| + | draw(d--c, dotted); | ||
| + | </asy> | ||
| + | |||
| + | As illustrated in the above diagram, drop a perpendicular from <math>D</math> onto the base at <math>P</math>. Denote the center of the base by <math>O</math>. By symmetry, <math>P</math> must be on <math>AO</math>. Now we need to find <math>DP</math>. | ||
| + | |||
| + | Apply Pythagorean theorem to <math>\triangle DPA</math> we have | ||
| + | <cmath> DP^2 = AD^2 - AP^2.</cmath> | ||
| + | |||
| + | Apply Pythagorean theorem to <math>\triangle DPC</math> and then <math>\triangle CPO</math> we have | ||
| + | <cmath> DP^2 = DC^2 - CP^2 = DC^2 - (CO^2 + OP^2) = DC^2 - (CO^2 + (AO-AP)^2) = DC^2 - CO^2 - (AO-AP)^2.</cmath> | ||
| + | |||
| + | Combining the above two, we have | ||
| + | <cmath>AD^2 - AP^2 = DC^2 - CO^2 - (AO-AP)^2.</cmath> | ||
| + | |||
| + | Since <math>AD=\sqrt{13}</math>, <math>DC=\sqrt{21}</math>, <math>CO=\frac{\sqrt{21}}{2}</math>, <math>AO=\frac{\sqrt{31}}{2}</math>, plug them into the above equation and solve for the only unknown variable <math>AP</math>, we get <math>AP=\frac{5}{\sqrt{31}}.</math> | ||
| + | |||
| + | Thus the height | ||
| + | <cmath> DP = \sqrt{AD^2 - AP^2} = \sqrt{13 - \frac{25}{31}} = \sqrt{\frac{378}{31}}. </cmath> | ||
| + | |||
| + | <asy> | ||
| + | unitsize(2cm); | ||
| + | pair a = (0, 0), b = (1, 0), c = 0.8*dir(40), d = 0.7*dir(80), e = c+d, p = 0.9*dir(10), o = (b+c)/2; | ||
| + | |||
| + | label("A'",a,S); | ||
| + | label("B'",b,S); | ||
| + | label("C'",c,W); | ||
| + | label("E'",e,N); | ||
| + | label("P'",p,S); | ||
| + | label("O'",o,W); | ||
| + | |||
| + | draw(a--b--(b+c)); | ||
| + | draw(a--c--(b+c), dotted); | ||
| + | draw(shift(d)*(a--b--(b+c)--c--cycle)); | ||
| + | draw(a--d); | ||
| + | draw(b--(b+d)); | ||
| + | draw(c--(c+d), dotted); | ||
| + | draw((b+c)--(b+c+d)); | ||
| + | |||
| + | draw(e--p, dotted); | ||
| + | draw(c--b, dotted); | ||
| + | draw(a--(b+c), dotted); | ||
| + | draw(p--a, dotted); | ||
| + | draw(e--a, dotted); | ||
| + | </asy> | ||
| + | |||
| + | For the other parallelepiped, using the same approach and drop a perpendicular from <math>E'</math> onto the base at <math>P'</math>. Similarly applying Pythagorean theorem to <math>\triangle E'P'C'</math>, <math>\triangle E'P'A'</math> and <math>\triangle A'P'O'</math> we have | ||
| + | <cmath>C'E'^2 - C'P'^2 = A'E'^2 - A'O'^2 - (C'P'-C'O')^2.</cmath> | ||
| + | |||
| + | Plugging known values into the above equation and solve for the only unknown variable <math>C'P'</math>, we get <math>C'P'=\frac{5}{\sqrt{21}}.</math> | ||
| + | |||
| + | Thus the height | ||
| + | <cmath> E'P' = \sqrt{C'E'^2 - C'P'^2} = \sqrt{13 - \frac{25}{21}} = \sqrt{\frac{248}{21}}. </cmath> | ||
| + | |||
| + | The ratio between the two is therefore | ||
| + | <cmath> \frac{DP}{E'P'} = \frac{\sqrt{\frac{378}{31}}}{\sqrt{\frac{248}{21}}} = \sqrt{\frac{2\cdot3^3\cdot7}{31}\cdot\frac{3\cdot7}{2^3\cdot31}} = \frac{3^2\cdot7}{2\cdot31} = \frac{63}{62}</cmath>, giving <math>\boxed{125}</math>. | ||
| + | |||
| + | ~sgdzw | ||
| + | |||
| + | ==Solution 5 (Visual)== | ||
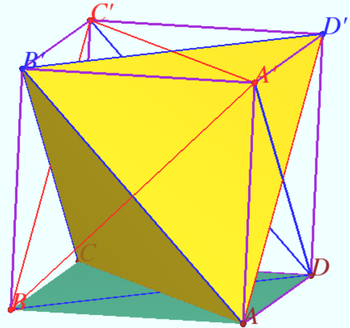
| + | [[File:2023 AIME I 13a.png|350px|right]] | ||
| + | Let us inscribe a tetrahedron <math>ACB'D'</math> in given parallelepiped so that its edges coincide with the diagonals of the faces of the parallelepiped. Note that the three edges outgoing from the vertex <math>B'</math> have the same length <math>b</math>, and the three edges at the base have a different length <math>a.</math> | ||
| + | |||
| + | The volume of the tetrahedron <math>V= \frac {a^2}{12}\sqrt{3b^2 - a^2}</math> is three times less than the volume of the parallelepiped. | ||
| + | |||
| + | In second parallelepiped <math>a</math> and <math>b</math> change the positions. | ||
| + | |||
| + | Required ratio is <math>\frac {a^2 \cdot \sqrt {3b^2 - a^2}}{b^2 \cdot \sqrt {3a^2 - b^2}} = \frac {21 \sqrt {3 \cdot 31 - 21}}{31 \cdot \sqrt{3 \cdot 21 - 31}} = \frac {21 \sqrt {72}}{31 \sqrt {32}}= \frac {63}{62}.</math> | ||
| + | |||
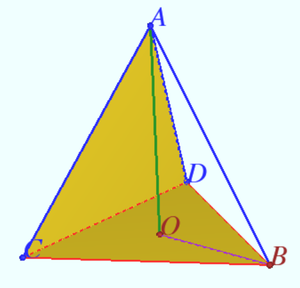
| + | <i><b>Claim</b></i> | ||
| + | [[File:2023 AIME I 13.png|300px|right]] | ||
| + | Let <math>ABCD</math> be the regular pyramid, <math>AB = AC = AD = b, BC = BD = CD = a.</math> | ||
| + | |||
| + | The area of <math>\triangle BCD = \frac {a^2 \sqrt {3}}{4}.</math> | ||
| + | |||
| + | Height <math>AO^2 = AB^2 - OB^2 = {b^2 - \frac {a^2}{3}}.</math> | ||
| + | |||
| + | Volume <math>V= \frac {a^2}{12}\sqrt{3b^2 - a^2}.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 6== | ||
| + | |||
| + | <asy> | ||
| + | unitsize(2cm); | ||
| + | pair a = (0, 0), b = (1, 0), c = 0.8*dir(40), d = dir(70), p = 0.33*dir(20), o = (b+c)/2, x = (0.2, 0); | ||
| + | |||
| + | label("A",a,S); | ||
| + | label("B",b,S); | ||
| + | label("C",c,S); | ||
| + | label("D",d,N); | ||
| + | label("X",x,S); | ||
| + | |||
| + | draw(a--b--(b+c)); | ||
| + | draw(a--c--(b+c), dotted); | ||
| + | draw(shift(d)*(a--b--(b+c)--c--cycle)); | ||
| + | draw(a--d); | ||
| + | draw(b--(b+d)); | ||
| + | draw(d--x); | ||
| + | draw(x--c, dotted); | ||
| + | draw(c--(c+d), dotted); | ||
| + | draw((b+c)--(b+c+d)); | ||
| + | |||
| + | </asy> | ||
| + | |||
| + | Let <math>\angle CAB</math> be acute and let <math>X</math> be the foot of the altitude from <math>C</math> to <math>AB</math>. Notice that this also implies that <math>X</math> is the foot of the altitude from <math>D</math> to <math>AB</math>. Now <math>\sqrt{13} \cdot CX = AB \cdot CX = \frac{1}{2} \sqrt{21} \cdot \sqrt{31}</math> so <math>CX = \frac{\sqrt{21} \cdot \sqrt{31}}{2 \sqrt{13}}</math> and <math>DX</math> is the same. <math>CD</math> must either be <math>\sqrt{21}</math> or <math>\sqrt{31}</math> because it is a diagonal. If <math>CD = \sqrt{21}</math>, applying the Law of Cosines on <math>\angle DXC</math>, <math>\cos \angle DXC = -\frac{5}{21}</math> so <math>\sin \angle DXC = \sqrt{\frac{416}{441}}</math>. If <math>CD = \sqrt{31}</math>, <math>\cos \angle DXC = \frac{5}{31}</math>, so <math>\sin \angle DXC = \sqrt{\frac{936}{961}}</math>. The ratios of the two parallelepipeds is equal to the ratios of the heights (since the bases are the same) which is equal to the ratio of the sines. Therefore it is <cmath> \frac{\sqrt{\frac{936}{961}}}{\sqrt{\frac{416}{441}}} = \sqrt{\frac{936}{416}} \cdot \frac{21}{31} = \frac{3}{2} \cdot \frac{21}{31} = \frac{63}{62} </cmath> so the answer is <math>63 + 62 = \boxed{125}</math>. | ||
| + | |||
| + | ==Video Solution== | ||
| + | |||
| + | https://youtu.be/5mJ6EqdFD94 | ||
| + | |||
| + | ~MathProblemSolvingSkills.com | ||
| + | |||
| + | |||
| + | |||
| + | ==Animated Video Solution== | ||
| + | |||
| + | https://youtu.be/VvCl5KIqT9M | ||
| + | |||
| + | ~Star League (https://starleague.us) | ||
| + | |||
| + | {{AIME box|year=2023|n=I|num-b=12|num-a=14}} | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | [[Category:3D Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 20:25, 5 September 2024
Contents
Problem
Each face of two noncongruent parallelepipeds is a rhombus whose diagonals have lengths ![]() and
and ![]() .
The ratio of the volume of the larger of the two polyhedra to the volume of the smaller is
.
The ratio of the volume of the larger of the two polyhedra to the volume of the smaller is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() . A parallelepiped is a solid with six parallelogram faces
such as the one shown below.
. A parallelepiped is a solid with six parallelogram faces
such as the one shown below.
![[asy] unitsize(2cm); pair o = (0, 0), u = (1, 0), v = 0.8*dir(40), w = dir(70); draw(o--u--(u+v)); draw(o--v--(u+v), dotted); draw(shift(w)*(o--u--(u+v)--v--cycle)); draw(o--w); draw(u--(u+w)); draw(v--(v+w), dotted); draw((u+v)--(u+v+w)); [/asy]](http://latex.artofproblemsolving.com/b/c/c/bcc8a67600e8a557236d37e2d01ae1737ef052b5.png)
Solution 1 (3-D Vector Analysis)
Denote ![]() .
Denote by
.
Denote by ![]() the length of each side of a rhombus.
the length of each side of a rhombus.
Now, we put the solid to the 3-d coordinate space.
We put the bottom face on the ![]() plane.
For this bottom face, we put a vertex with an acute angle
plane.
For this bottom face, we put a vertex with an acute angle ![]() at the origin, denoted as
at the origin, denoted as ![]() .
For two edges that are on the bottom face and meet at
.
For two edges that are on the bottom face and meet at ![]() , we put one edge on the positive side of the
, we put one edge on the positive side of the ![]() -axis. The endpoint is denoted as
-axis. The endpoint is denoted as ![]() . Hence,
. Hence, ![]() .
We put the other edge in the first quadrant of the
.
We put the other edge in the first quadrant of the ![]() plane. The endpoint is denoted as
plane. The endpoint is denoted as ![]() . Hence,
. Hence, ![]() .
.
For the third edge that has one endpoint ![]() , we denote by
, we denote by ![]() its second endpoint.
We denote
its second endpoint.
We denote ![]() .
Without loss of generality, we set
.
Without loss of generality, we set ![]() .
Hence,
.
Hence,
![]()
We have
 and
and

Case 1: ![]() or
or ![]() .
.
By solving (2) and (3), we get

Plugging these into (1), we get

Case 2: ![]() and
and ![]() , or
, or ![]() and
and ![]() .
.
By solving (2) and (3), we get

Plugging these into (1), we get

We notice that ![]() . Thus, (4) (resp. (5)) is the parallelepiped with a larger (resp. smaller) height.
. Thus, (4) (resp. (5)) is the parallelepiped with a larger (resp. smaller) height.
Therefore, the ratio of the volume of the larger parallelepiped to the smaller one is

Recall that ![]() .
Thus,
.
Thus, ![]() .
Plugging this into the equation above, we get
.
Plugging this into the equation above, we get
![]()
Therefore, the answer is ![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 2 (no trig)
Let one of the vertices be at the origin and the three adjacent vertices be ![]() ,
, ![]() , and
, and ![]() . For one of the parallelepipeds, the three diagonals involving the origin have length
. For one of the parallelepipeds, the three diagonals involving the origin have length ![]() . Hence,
. Hence, ![]() and
and ![]() . Since all of
. Since all of ![]() ,
, ![]() , and
, and ![]() have equal length,
have equal length, ![]() ,
, ![]() , and
, and ![]() . Symmetrically,
. Symmetrically, ![]() ,
, ![]() , and
, and ![]() . Hence the volume of the parallelepiped is given by
. Hence the volume of the parallelepiped is given by  .
.
For the other parallelepiped, the three diagonals involving the origin are of length ![]() and the volume is
and the volume is  .
.
Consequently, the answer is ![]() , giving
, giving ![]() .
.
~EVIN-
Solution 3 (No trig, no linear algebra)
Observe that both parallelepipeds have two vertices (one on each base) that have three congruent angles meeting at them. Denote the parallelepiped with three acute angles meeting ![]() , and the one with three obtuse angles meeting
, and the one with three obtuse angles meeting ![]() .
.
The area of a parallelepiped is simply the base area times the height, but because both parallelepipeds have the same base, what we want is just the ratio of the heights.
Denote the point with three acute angles meeting at it in ![]() as
as ![]() , and its neighbors
, and its neighbors ![]() ,
, ![]() , and
, and ![]() . Similarly, denote the point with three obtuse angles meeting at it in
. Similarly, denote the point with three obtuse angles meeting at it in ![]() as
as ![]() , and its neighbors
, and its neighbors ![]() ,
, ![]() , and
, and ![]() .
.
We have the following equations:
![]()
![]()
However, ![]() and
and ![]() are both half the area of a rhombus with diagonals
are both half the area of a rhombus with diagonals ![]() and
and ![]() , so our ratio is really
, so our ratio is really
![]()
Because the diagonals of all of the faces are ![]() and
and ![]() , each edge of the parallelepipeds is
, each edge of the parallelepipeds is ![]() by the Pythagorean theorem.
by the Pythagorean theorem.
We have ![]() , and
, and ![]() . When we drop a perpendicular to the centroid of
. When we drop a perpendicular to the centroid of ![]() from
from ![]() (let's call this point
(let's call this point ![]() ), we have
), we have ![]() . Thus,
. Thus,
![]()
![]()
![]()
The area of base ![]() is
is ![]() . Hence,
. Hence,
![]()
![]()
We can apply a similar approach to ![]() .
.
![]() , and
, and ![]() . When we drop a perpendicular to the centroid of
. When we drop a perpendicular to the centroid of ![]() from
from ![]() (let's call this point
(let's call this point ![]() ), we have
), we have ![]() . Thus,
. Thus,
![]()
![]()
![]()
The area of base ![]() is
is ![]() . Hence,
. Hence,
![]()
![]()
![]()
Finally,
![\[\frac{P}{P'} = \frac{\textrm{Vol}(ABCD)}{\textrm{Vol}(A'B'C'D')} = \frac{\frac{63\sqrt{2}}{12}}{\frac{62\sqrt{2}}{12}} = \frac{63}{62}.\]](http://latex.artofproblemsolving.com/a/b/8/ab833824abd250a9c73928f8ebe90ecdff1158b4.png)
Our answer is ![]() .
.
~mathboy100
Solution 4 (Pythagorean theorem)
Since the two parallelepipeds have the same base, all we need to do is to find their respective heights.
![[asy] unitsize(2cm); pair a = (0, 0), b = (1, 0), c = 0.8*dir(40), d = dir(70), p = 0.33*dir(20), o = (b+c)/2; label("A",a,S); label("B",b,S); label("C",c,S); label("D",d,N); label("P",p,S); label("O",o,E); draw(a--b--(b+c)); draw(a--c--(b+c), dotted); draw(shift(d)*(a--b--(b+c)--c--cycle)); draw(a--d); draw(b--(b+d)); draw(c--(c+d), dotted); draw((b+c)--(b+c+d)); draw(d--p, dotted); draw(c--b, dotted); draw(a--(b+c), dotted); draw(p--c, dotted); draw(d--c, dotted); [/asy]](http://latex.artofproblemsolving.com/e/0/2/e0213dedd5d44e21378f2bee16a0224684408ca6.png)
As illustrated in the above diagram, drop a perpendicular from ![]() onto the base at
onto the base at ![]() . Denote the center of the base by
. Denote the center of the base by ![]() . By symmetry,
. By symmetry, ![]() must be on
must be on ![]() . Now we need to find
. Now we need to find ![]() .
.
Apply Pythagorean theorem to ![]() we have
we have
![]()
Apply Pythagorean theorem to ![]() and then
and then ![]() we have
we have
![]()
Combining the above two, we have
![]()
Since ![]() ,
, ![]() ,
, ![]() ,
, ![]() , plug them into the above equation and solve for the only unknown variable
, plug them into the above equation and solve for the only unknown variable ![]() , we get
, we get ![]()
Thus the height
![]()
![[asy] unitsize(2cm); pair a = (0, 0), b = (1, 0), c = 0.8*dir(40), d = 0.7*dir(80), e = c+d, p = 0.9*dir(10), o = (b+c)/2; label("A'",a,S); label("B'",b,S); label("C'",c,W); label("E'",e,N); label("P'",p,S); label("O'",o,W); draw(a--b--(b+c)); draw(a--c--(b+c), dotted); draw(shift(d)*(a--b--(b+c)--c--cycle)); draw(a--d); draw(b--(b+d)); draw(c--(c+d), dotted); draw((b+c)--(b+c+d)); draw(e--p, dotted); draw(c--b, dotted); draw(a--(b+c), dotted); draw(p--a, dotted); draw(e--a, dotted); [/asy]](http://latex.artofproblemsolving.com/f/3/6/f36c54fb3298b5bf80f934cf31a802f7128459cd.png)
For the other parallelepiped, using the same approach and drop a perpendicular from ![]() onto the base at
onto the base at ![]() . Similarly applying Pythagorean theorem to
. Similarly applying Pythagorean theorem to ![]() ,
, ![]() and
and ![]() we have
we have
![]()
Plugging known values into the above equation and solve for the only unknown variable ![]() , we get
, we get ![]()
Thus the height
![]()
The ratio between the two is therefore
![\[\frac{DP}{E'P'} = \frac{\sqrt{\frac{378}{31}}}{\sqrt{\frac{248}{21}}} = \sqrt{\frac{2\cdot3^3\cdot7}{31}\cdot\frac{3\cdot7}{2^3\cdot31}} = \frac{3^2\cdot7}{2\cdot31} = \frac{63}{62}\]](http://latex.artofproblemsolving.com/7/3/0/73068f51f166d3b0c4ac6c609f527d31dafc926c.png) , giving
, giving ![]() .
.
~sgdzw
Solution 5 (Visual)
Let us inscribe a tetrahedron ![]() in given parallelepiped so that its edges coincide with the diagonals of the faces of the parallelepiped. Note that the three edges outgoing from the vertex
in given parallelepiped so that its edges coincide with the diagonals of the faces of the parallelepiped. Note that the three edges outgoing from the vertex ![]() have the same length
have the same length ![]() , and the three edges at the base have a different length
, and the three edges at the base have a different length ![]()
The volume of the tetrahedron ![]() is three times less than the volume of the parallelepiped.
is three times less than the volume of the parallelepiped.
In second parallelepiped ![]() and
and ![]() change the positions.
change the positions.
Required ratio is ![]()
Claim
Let ![]() be the regular pyramid,
be the regular pyramid, ![]()
The area of ![]()
Height ![]()
Volume ![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 6
![[asy] unitsize(2cm); pair a = (0, 0), b = (1, 0), c = 0.8*dir(40), d = dir(70), p = 0.33*dir(20), o = (b+c)/2, x = (0.2, 0); label("A",a,S); label("B",b,S); label("C",c,S); label("D",d,N); label("X",x,S); draw(a--b--(b+c)); draw(a--c--(b+c), dotted); draw(shift(d)*(a--b--(b+c)--c--cycle)); draw(a--d); draw(b--(b+d)); draw(d--x); draw(x--c, dotted); draw(c--(c+d), dotted); draw((b+c)--(b+c+d)); [/asy]](http://latex.artofproblemsolving.com/5/3/d/53d84202e9fc92c8e25af8e9eea7d41f1d904224.png)
Let ![]() be acute and let
be acute and let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() to
to ![]() . Notice that this also implies that
. Notice that this also implies that ![]() is the foot of the altitude from
is the foot of the altitude from ![]() to
to ![]() . Now
. Now ![]() so
so ![]() and
and ![]() is the same.
is the same. ![]() must either be
must either be ![]() or
or ![]() because it is a diagonal. If
because it is a diagonal. If ![]() , applying the Law of Cosines on
, applying the Law of Cosines on ![]() ,
, ![]() so
so ![]() . If
. If ![]() ,
, ![]() , so
, so ![]() . The ratios of the two parallelepipeds is equal to the ratios of the heights (since the bases are the same) which is equal to the ratio of the sines. Therefore it is
. The ratios of the two parallelepipeds is equal to the ratios of the heights (since the bases are the same) which is equal to the ratio of the sines. Therefore it is ![\[\frac{\sqrt{\frac{936}{961}}}{\sqrt{\frac{416}{441}}} = \sqrt{\frac{936}{416}} \cdot \frac{21}{31} = \frac{3}{2} \cdot \frac{21}{31} = \frac{63}{62}\]](http://latex.artofproblemsolving.com/4/3/c/43c6804cabef547df0fb2efe5bf7131c35ca51ee.png) so the answer is
so the answer is ![]() .
.
Video Solution
~MathProblemSolvingSkills.com
Animated Video Solution
~Star League (https://starleague.us)
| 2023 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.