Difference between revisions of "Nine-point circle"

Latest revision as of 15:02, 12 March 2024

Triangle ABC with the nine-point circle in light orange

The nine-point circle (also known as Euler's circle or Feuerbach's circle) of a given triangle is a circle which passes through 9 "significant" points:

The three feet of the altitudes of the triangle.
The three midpoints of the edges of the triangle.
The three midpoints of the segments joining the vertices of the triangle to its orthocenter. (These points are sometimes known as the Euler points of the triangle.)

"The nine-point circle is tangent to the incircle, has a radius equal to half the circumradius, and its center is the midpoint of the segment connecting the orthocenter and the circumcenter." -hankinjg

That such a circle exists is a non-trivial theorem of Euclidean geometry.

The center of the nine-point circle is the nine-point center and is usually denoted $N$ .

The nine-point circle is tangent to the incircle, has a radius equal to half the circumradius, and its center is the midpoint of the segment connecting the orthocenter and the circumcenter, upon which the centroid also falls.

It's also denoted Kimberling center $X_5$ .

First Proof of Existence

Since $O_c$ is the midpoint of $AB$ and $E_b$ is the midpoint of $BH$ , $O_cE_b$ is parallel to $AH$ . Using similar logic, we see that $O_bE_c$ is also parallel to $AH$ . Since $E_b$ is the midpoint of $HB$ and $E_c$ is the midpoint of $HC$ , $E_bE_c$ is parallel to $BC$ , which is perpendicular to $AH$ . Similar logic gives us that $O_bO_c$ is perpendicular to $AH$ as well. Therefore $O_bO_cE_bE_c$ is a rectangle, which is a cyclic figure. The diagonals $O_bE_b$ and $O_cE_c$ are diagonals of the circumcircle. Similar logic to the above gives us that $O_aO_cE_aE_c$ is a rectangle with a common diagonal to $O_bO_cE_bE_c$ . Therefore the circumcircles of the two rectangles are identical. We can also gain that rectangle $O_aO_bE_aE_b$ is also on the circle.

We now have a circle with the points $O_a$ , $O_b$ , $O_c$ , $E_a$ , $E_b$ , and $E_c$ on it, with diameters $O_aE_A$ , $O_bE_b$ , and $O_cE_c$ . We now note that $\angle E_aH_aO_a=\angle E_bH_bO_b=\angle E_cH_cO_c=90^{\circ}$ . Therefore $H_a$ , $H_b$ , and $H_c$ are also on the circle. We now have a circle with the midpoints of the sides on it, the three midpoints of the segments joining the vertices of the triangle to its orthocenter on it, and the three feet of the altitudes of the triangle on it. Therefore, the nine points are on the circle, and the nine-point circle exists.

Second Proof of Existence

We know that the reflection of the orthocenter about the sides and about the midpoints of the triangle's sides lie on the circumcircle. Thus, consider the homothety centered at $H$ with ratio ${1}/{2}$ . It maps the circumcircle of $\triangle ABC$ to the nine-point circle, and the vertices of the triangle to its Euler points. Hence proved.

Common Euler circle

Let an acute-angled triangle $ABC$ with orthocenter $H$ be given.

$\Omega = \odot ABC, Z$ be the point on $\Omega$ opposite $A.$

Points $E \in AB$ and $F \in AC$ such that $AEHF$ is a parallelogram. The line $EF$ intersects $\Omega$ at the points $X$ and $Y.$

Prove that triangles $\triangle ABC$ and $\triangle XYZ$ has common Euler (nine-point) circle.

Proof $BH \perp AC, EH||AF \implies BH \perp EH, \angle BEH = \angle BAC.$ $CH \perp AB, FH||AE \implies CH \perp FH, \angle CFH = \angle BAC.$ $\triangle BHE \sim \triangle CHF \implies \frac{AF}{BE} = \frac{EH}{BE} = \frac{FH}{FC} = \frac{AE}{FC}.$ $XE \cdot EY = AE \cdot BE = AF \cdot FC = XF \cdot FY \implies$ $XE \cdot (EF + FY) = (XE + EF) \cdot FY \implies XE = FY.$ Denote $D$ is midpoint $AH \implies DX = DE + XE = DF + FY = DY.$

Let’s consider $\triangle AHZ.$ Circumcenter of $\triangle ABC$ point $O$ is the midpoint $AZ,$ point $D$ is the midpoint $AH.$

Denote $G$ the centroid of $\triangle AHZ, G = ZD \cup HO \implies \frac {HG} {GO} = 2 \implies$

$G$ is the centroid of $\triangle ABC.$

Denote $M$ the midpoint of $BC. \frac {AG} {GM} = 2 \implies M$ is the midpoint of $HZ.$

$\frac {ZG} {GD} = 2 \implies G$ is the centroid of $\triangle XYZ.$

Point $O$ is the circumcenter of $\triangle XYZ \implies H$ is the orthocenter of $\triangle XYZ.$

The triangles $\triangle ABC$ and $\triangle XYZ$ has common circumcircle and common center of Euler circle (the midpoint of $OH$ ) therefore these triangles has the common Euler circle.

vladimir.shelomovskii@gmail.com, vvsss

@@ Line 19: / Line 19: @@
 ==First Proof of Existence==
-Since <math>O_c</math> is the midpoint of <math>AB</math> and <math>E_b</math> is the midpoint of <math>BH</math>, <math>O_cE_b</math> is parallel to <math>AH</math>. Using similar logic, we can also see that <math>O_bE_c</math> is also parallel to <math>AH</math>. Since <math>E_b</math> is the midpoint of <math>HB</math> and <math>E_c</math> is the midpoint of <math>HC</math>, <math>E_bE_c</math> is parallel to <math>BC</math>, which is perpendicular to <math>AH</math>. Similar logic gives us that <math>O_bO_c</math> is perpendicular to <math>AH</math> as well. Therefore <math>O_bO_cE_bE_c</math> is a rectangle, which is a cyclic figure. The diagonals <math>O_bE_b</math> and <math>O_cE_c</math> are diagonals of the circumcircle. Similar logic to the above gives us that <math>O_aO_cE_aE_c</math> is a rectangle with a common diagonal to <math>O_bO_cE_bE_c</math>. Therefore the circumcircles of the two rectangles are identical. We can also gain that rectangle <math>O_aO_bE_aE_b</math> is also on the circle.
+Since <math>O_c</math> is the midpoint of <math>AB</math> and <math>E_b</math> is the midpoint of <math>BH</math>, <math>O_cE_b</math> is parallel to <math>AH</math>. Using similar logic, we see that <math>O_bE_c</math> is also parallel to <math>AH</math>. Since <math>E_b</math> is the midpoint of <math>HB</math> and <math>E_c</math> is the midpoint of <math>HC</math>, <math>E_bE_c</math> is parallel to <math>BC</math>, which is perpendicular to <math>AH</math>. Similar logic gives us that <math>O_bO_c</math> is perpendicular to <math>AH</math> as well. Therefore <math>O_bO_cE_bE_c</math> is a rectangle, which is a cyclic figure. The diagonals <math>O_bE_b</math> and <math>O_cE_c</math> are diagonals of the circumcircle. Similar logic to the above gives us that <math>O_aO_cE_aE_c</math> is a rectangle with a common diagonal to <math>O_bO_cE_bE_c</math>. Therefore the circumcircles of the two rectangles are identical. We can also gain that rectangle <math>O_aO_bE_aE_b</math> is also on the circle.
 We now have a circle with the points <math>O_a</math>, <math>O_b</math>, <math>O_c</math>, <math>E_a</math>, <math>E_b</math>, and <math>E_c</math> on it, with diameters <math>O_aE_A</math>, <math>O_bE_b</math>, and <math>O_cE_c</math>. We now note that <math>\angle E_aH_aO_a=\angle E_bH_bO_b=\angle E_cH_cO_c=90^{\circ}</math>. Therefore <math>H_a</math>, <math>H_b</math>, and <math>H_c</math> are also on the circle. We now have a circle with the midpoints of the sides on it, the three midpoints of the segments joining the vertices of the triangle to its orthocenter on it, and the three feet of the altitudes of the triangle on it. Therefore, the nine points are on the circle, and the nine-point circle exists.
@@ Line 26: / Line 26: @@
 We know that the reflection of the orthocenter about the sides and about the midpoints of the triangle's sides lie on the circumcircle. Thus, consider the homothety centered at <math>H</math> with ratio <math>{1}/{2}</math>. It maps the circumcircle of <math>\triangle ABC</math> to the nine-point circle, and the vertices of the triangle to its [[Euler point]]s.
 Hence proved.
+==Common Euler circle==
+[[File:Double orthocenter.png|370px|right]]
+[[File:Double orthocenter 1.png|370px|right]]
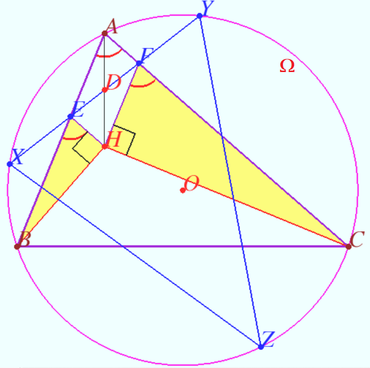
+Let an acute-angled triangle <math>ABC</math> with orthocenter <math>H</math> be given.
+<math>\Omega = \odot ABC, Z</math> be the point on <math>\Omega</math> opposite <math>A.</math>
+Points <math>E \in AB</math> and <math>F \in AC</math> such that <math>AEHF</math> is a parallelogram. The line <math>EF</math> intersects <math>\Omega</math> at the points <math>X</math> and <math>Y.</math>
+Prove that triangles <math>\triangle ABC</math> and <math>\triangle XYZ</math> has common Euler (nine-point) circle.
+<i><b>Proof</b></i>
+<cmath>BH \perp AC, EH||AF \implies BH \perp EH, \angle BEH = \angle BAC.</cmath>
+<cmath>CH \perp AB, FH||AE \implies CH \perp FH, \angle CFH = \angle BAC.</cmath>
+<cmath>\triangle BHE \sim \triangle CHF \implies \frac{AF}{BE} = \frac{EH}{BE} =  \frac{FH}{FC} = \frac{AE}{FC}.</cmath>
+<cmath> XE \cdot EY = AE \cdot BE = AF \cdot FC = XF \cdot FY \implies</cmath>
+<cmath> XE \cdot (EF + FY) =  (XE + EF)  \cdot FY \implies XE = FY.</cmath>
+Denote <math>D</math> is midpoint <math>AH \implies DX = DE + XE = DF + FY = DY.</math>
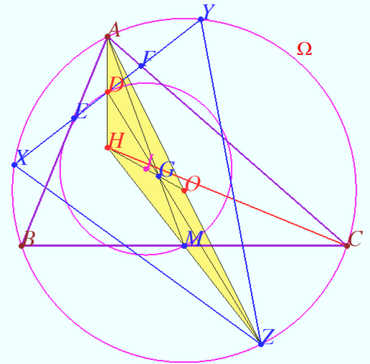
+Let’s consider <math>\triangle AHZ.</math> Circumcenter of <math>\triangle ABC</math> point <math>O</math> is the midpoint <math>AZ,</math> point <math>D</math> is the midpoint <math>AH.</math>
+Denote <math>G</math> the centroid of <math>\triangle AHZ, G = ZD \cup HO \implies \frac {HG} {GO} = 2 \implies</math>
+<math>G</math> is the centroid of <math>\triangle ABC.</math>
+Denote <math>M</math> the midpoint of <math>BC. \frac {AG} {GM} = 2 \implies M</math> is the midpoint of <math>HZ.</math>
+<math>\frac {ZG} {GD} = 2 \implies G</math> is the centroid of <math>\triangle XYZ.</math>
+Point <math>O</math> is the circumcenter of <math>\triangle XYZ \implies H</math> is the orthocenter of <math>\triangle XYZ.</math>
+The triangles <math>\triangle ABC</math> and <math>\triangle XYZ</math> has common circumcircle and common center of Euler circle (the midpoint of <math>OH</math>) therefore these triangles has the common Euler circle.
+'''vladimir.shelomovskii@gmail.com, vvsss'''
 ==See also==
 *[[Kimberling center]]

Page

Toolbox

Search

Difference between revisions of "Nine-point circle"

Latest revision as of 15:02, 12 March 2024

Contents

First Proof of Existence

Second Proof of Existence

Common Euler circle

See also