Difference between revisions of "2024 AIME I Problems/Problem 10"

Latest revision as of 14:03, 5 October 2024

Problem

Let $ABC$ be a triangle inscribed in circle $\omega$ . Let the tangents to $\omega$ at $B$ and $C$ intersect at point $D$ , and let $\overline{AD}$ intersect $\omega$ at $P$ . If $AB=5$ , $BC=9$ , and $AC=10$ , $AP$ can be written as the form $\frac{m}{n}$ , where $m$ and $n$ are relatively prime integers. Find $m + n$ .

Diagram

$[asy] import olympiad; unitsize(15); pair A, B, C, D, E, F, P, O; C = origin; A = (10,0); B = (7.8, 4.4899); draw(A--B--C--cycle); draw(A..B..C..cycle, red+dotted); O = circumcenter(A, B, C); E = rotate(90,B) * (O); F = rotate(90,C) * (O); D = IP(B..E + (B-E)*4, C..F + (C-F)*-3); draw(B--D--C--D--A); P = IP(D..A, A..B..C); dot(A); dot(B); dot(C); dot(D); dot(P); label("$A$", A, dir(335)); label("$B$", B, dir(65)); label("$C$", C, dir(200)); label("$D$", D, dir(135)); label("$P$", P, dir(235)); [/asy]$

Solution 1

From the tangency condition we have $\let\angle BCD = \let\angle CBD = \let\angle A$ . With LoC we have $\cos(A) = \frac{25+100-81}{2*5*10} = \frac{11}{25}$ and $\cos(B) = \frac{81+25-100}{2*9*5} = \frac{1}{15}$ . Then, $CD = \frac{\frac{9}{2}}{\cos(A)} = \frac{225}{22}$ . Using LoC we can find $AD$ : $AD^2 = AC^2 + CD^2 - 2(AC)(CD)\cos(A+C) = 10^2+(\frac{225}{22})^2 + 2(10)\frac{225}{22}\cos(B) = 100 + \frac{225^2}{22^2} + 2(10)\frac{225}{22}*\frac{1}{15} = \frac{5^4*13^2}{484}$ . Thus, $AD = \frac{5^2*13}{22}$ . By Power of a Point, $DP*AD = CD^2$ so $DP*\frac{5^2*13}{22} = (\frac{225}{22})^2$ which gives $DP = \frac{5^2*9^2}{13*22}$ . Finally, we have $AP = AD - DP = \frac{5^2*13}{22} - \frac{5^2*9^2}{13*22} = \frac{100}{13} \rightarrow \boxed{113}$ .

~angie.

Solution 2

We know $AP$ is the symmedian,(see Symmedian and tangents )

which implies $\triangle{ABP}\sim \triangle{AMC}$ where $M$ is the midpoint of $BC$ .

By Appolonius theorem, $AM=\frac{13}{2}$ .

Thus, we have $\frac{AP}{AC}=\frac{AB}{AM}, AP=\frac{100}{13}\implies \boxed{113}$

~Bluesoul

Solution 3

Extend sides $\overline{AB}$ and $\overline{AC}$ to points $E$ and $F$ , respectively, such that $B$ and $C$ are the feet of the altitudes in $\triangle AEF$ . Denote the feet of the altitude from $A$ to $\overline{EF}$ as $X$ , and let $H$ denote the orthocenter of $\triangle AEF$ . Call $M$ the midpoint of segment $\overline{EF}$ . By the Three Tangents Lemma, we have that $MB$ and $MC$ are both tangents to $(ABC)$ $\implies$ $M = D$ , and since $M$ is the midpoint of $\overline{EF}$ , $MF = MB$ . Additionally, by angle chasing, we get that: $\angle ABC \cong \angle AHC \cong \angle EHX$ Also, $\angle EHX = 90 ^\circ - \angle HEF = 90 ^\circ - (90 ^\circ - \angle AFE) = \angle AFE$ Furthermore, $AB = AF \cdot \cos(A)$ From this, we see that $\triangle ABC \sim \triangle AFE$ with a scale factor of $\cos(A)$ . By the Law of Cosines, $\cos(A) = \frac{10^2 + 5^2 - 9^2}{2 \cdot 10 \cdot 5} = \frac{11}{25}$ Thus, we can find that the side lengths of $\triangle AEF$ are $\frac{250}{11}, \frac{125}{11}, \frac{225}{11}$ . Then, by Stewart's theorem, $AM = \frac{13 \cdot 25}{22}$ . By Power of a Point, $\overline{MB} \cdot \overline{MB} = \overline{MA} \cdot \overline{MP}$ $\frac{225}{22} \cdot \frac{225}{22} = \overline{MP} \cdot \frac{13 \cdot 25}{22} \implies \overline{MP} = \frac{225 \cdot 9}{22 \cdot 13}$ Thus, $AP = AM - MP = \frac{13 \cdot 25}{22} - \frac{225 \cdot 9}{22 \cdot 13} = \frac{100}{13}$ Therefore, the answer is $\boxed{113}$ .

~mathwiz_1207

Solution 4 (LoC spam)

Connect lines $\overline{PB}$ and $\overline{PC}$ . From the angle by tanget formula, we have $\angle PBD = \angle DAB$ . Therefore by AA similarity, $\triangle PBD \sim \triangle BAD$ . Let $\overline{BP} = x$ . Using ratios, we have $\frac{x}{5}=\frac{BD}{AD}.$ Similarly, using angle by tangent, we have $\angle PCD = \angle DAC$ , and by AA similarity, $\triangle CPD \sim \triangle ACD$ . By ratios, we have $\frac{PC}{10}=\frac{CD}{AD}.$ However, because $\overline{BD}=\overline{CD}$ , we have $\frac{x}{5}=\frac{PC}{10},$ so $\overline{PC}=2x.$ Now using Law of Cosines on $\angle BAC$ in triangle $\triangle ABC$ , we have $9^2=5^2+10^2-100\cos(\angle BAC).$ Solving, we find $\cos(\angle BAC)=\frac{11}{25}$ . Now we can solve for $x$ . Using Law of Cosines on $\triangle BPC,$ we have \begin{align*} 81&=x^2+4x^2-4x^2\cos(180-\angle BAC) \\ &= 5x^2+4x^2\cos(BAC). \\ \end{align*}

Solving, we get $x=\frac{45}{13}.$ Now we have a system of equations using Law of Cosines on $\triangle BPA$ and $\triangle CPA$ , $AP^2=5^2+\left(\frac{45}{13}\right)^2 -(10) \left(\frac{45}{13} \right)\cos(ABP)$ $AP^2=10^2+4 \left(\frac{45}{13} \right)^2 + (40) \left(\frac{45}{13} \right)\cos(ABP).$

Solving, we find $\overline{AP}=\frac{100}{13}$ , so our desired answer is $100+13=\boxed{113}$ .

~evanhliu2009

Solution 5

Following from the law of cosines, we can easily get $\cos A = \frac{11}{25}$ , $\cos B = \frac{1}{15}$ , $\cos C = \frac{13}{15}$ .

Hence, $\sin A = \frac{6 \sqrt{14}}{25}$ , $\cos 2C = \frac{113}{225}$ , $\sin 2C = \frac{52 \sqrt{14}}{225}$ . Thus, $\cos \left( A + 2C \right) = - \frac{5}{9}$ .

Denote by $R$ the circumradius of $\triangle ABC$ . In $\triangle ABC$ , following from the law of sines, we have $R = \frac{BC}{2 \sin A} = \frac{75}{4 \sqrt{14}}$ .

Because $BD$ and $CD$ are tangents to the circumcircle $ABC$ , $\triangle OBD \cong \triangle OCD$ and $\angle OBD = 90^\circ$ . Thus, $OD = \frac{OB}{\cos \angle BOD} = \frac{R}{\cos A}$ .

In $\triangle AOD$ , we have $OA = R$ and $\angle AOD = \angle BOD + \angle AOB = A + 2C$ . Thus, following from the law of cosines, we have

\begin{align*} AD & = \sqrt{OA^2 + OD^2 - 2 OA \cdot OD \cos \angle AOD} \\ & = \frac{26 \sqrt{14}}{33} R. \end{align*}

Following from the law of cosines,

\begin{align*} \cos \angle OAD & = \frac{AD^2 + OA^2 - OD^2}{2 AD \cdot OA} \\ & = \frac{8 \sqrt{14}}{39} . \end{align*}

Therefore,

\begin{align*} AP & = 2 OA \cos \angle OAD \\ & = \frac{100}{13} . \end{align*}

Therefore, the answer is $100 + 13 = \boxed{\textbf{(113) }}$ .

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution 1 by OmegaLearn.org

https://youtu.be/heryP002bp8

Video Solution

https://youtu.be/RawwQmVYyaw

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 6

Note that since P is a symmedian, $(AP;BC)$ are harmonic. As a result, $\frac{BP}{PC} = \frac{BA}{CA}$ . As a result, $2(BP) = PC$ . Call $BP = x$ . Then, $PC = 2x$ . Since $cos A = \frac{11}{25}$ , $cos BPC = - \frac{11}{25}$ . Use LOC to find $x = \frac{45}{13}$ . Finish with Ptolemy on ABPC, and finish to get $\frac{100}{13}$ .

@@ Line 1: / Line 1: @@
 ==Problem==
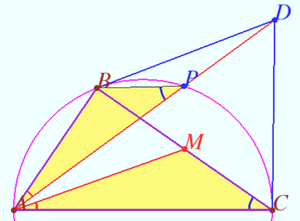
-Let <math>ABC</math> be a triangle inscribed in circle <math>\omega</math>. Let the tangents to <math>\omega</math> at <math>B</math> and <math>C</math> intersect at point <math>D</math>, and let <math>\overline{AD}</math> intersect <math>\omega</math> at <math>P</math>. Find <math>AP</math>, if <math>AB=5</math>, <math>BC=9</math>, and <math>AC=10</math>.
+Let <math>ABC</math> be a triangle inscribed in circle <math>\omega</math>. Let the tangents to <math>\omega</math> at <math>B</math> and <math>C</math> intersect at point <math>D</math>, and let <math>\overline{AD}</math> intersect <math>\omega</math> at <math>P</math>. If <math>AB=5</math>, <math>BC=9</math>, and <math>AC=10</math>, <math>AP</math> can be written as the form <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime integers. Find <math>m + n</math>.
+==Diagram==
+<asy>
+import olympiad;
+unitsize(15);
+pair A, B, C, D, E, F, P, O;
+C = origin; A = (10,0); B = (7.8, 4.4899);
+draw(A--B--C--cycle); draw(A..B..C..cycle, red+dotted);
+O = circumcenter(A, B, C);
+E = rotate(90,B) * (O);
+F = rotate(90,C) * (O);
+D = IP(B..E + (B-E)*4, C..F + (C-F)*-3);
+draw(B--D--C--D--A);
+P = IP(D..A, A..B..C);
+dot(A); dot(B); dot(C); dot(D); dot(P);
+label("$A$", A, dir(335));
+label("$B$", B, dir(65));
+label("$C$", C, dir(200));
+label("$D$", D, dir(135));
+label("$P$", P, dir(235));
+</asy>
 ==Solution 1==
@@ Line 8: / Line 38: @@
 ==Solution 2==
+[[File:2024 AIME I problem 10.png|300px|right]]
+We know <math>AP</math> is the symmedian,(see [[ Symmedians, Lemoine point | Symmedian and tangents ]])
-Well know <math>AP</math> is the symmedian, which implies <math>\triangle{ABP}\sim \triangle{AMC}</math> where <math>M</math> is the midpoint of <math>BC</math>. By Appolonius theorem, <math>AM=\frac{13}{2}</math>. Thus, we have <math>\frac{AP}{AC}=\frac{AB}{AM}, AP=\frac{100}{13}\implies \boxed{113}</math>
+which implies <math>\triangle{ABP}\sim \triangle{AMC}</math> where <math>M</math> is the midpoint of <math>BC</math>.
+By Appolonius theorem, <math>AM=\frac{13}{2}</math>.
+Thus, we have <math>\frac{AP}{AC}=\frac{AB}{AM}, AP=\frac{100}{13}\implies \boxed{113}</math>
 ~Bluesoul
@@ Line 15: / Line 51: @@
 ==Solution 3==
-Extend sides <math>\overline{AB}</math> and <math>\overline{AC}</math> to points <math>E</math> and <math>F</math>, respectively, such that <math>B</math> and <math>C</math> are the feet of the altitudes in <math>\triangle AEF</math>. Denote the feet of the altitude from <math>A</math> to <math>\overline{EF}</math> as <math>X</math>, and let <math>H</math> denote the orthocenter of <math>\triangle AEF</math>. Call <math>M</math> the midpoint of segment <math>\overline{EF}</math>. By the Three Tangents Lemma, we have that <math>MB</math> and <math>MC</math> are both tangents to <math>(ABC)</math> <math>\implies</math> <math>M = P</math>, and since <math>M</math> is the midpoint of <math>\overline{EF}</math>, <math>MF = MB</math>. Additionally, by angle chasing, we get that:
+Extend sides <math>\overline{AB}</math> and <math>\overline{AC}</math> to points <math>E</math> and <math>F</math>, respectively, such that <math>B</math> and <math>C</math> are the feet of the altitudes in <math>\triangle AEF</math>. Denote the feet of the altitude from <math>A</math> to <math>\overline{EF}</math> as <math>X</math>, and let <math>H</math> denote the orthocenter of <math>\triangle AEF</math>. Call <math>M</math> the midpoint of segment <math>\overline{EF}</math>. By the Three Tangents Lemma, we have that <math>MB</math> and <math>MC</math> are both tangents to <math>(ABC)</math> <math>\implies</math> <math>M = D</math>, and since <math>M</math> is the midpoint of <math>\overline{EF}</math>, <math>MF = MB</math>. Additionally, by angle chasing, we get that:
 <cmath>\angle ABC \cong \angle AHC \cong \angle EHX</cmath>
 Also,
@@ Line 24: / Line 60: @@
 <cmath>\cos(A) = \frac{10^2 + 5^2 - 9^2}{2 \cdot 10 \cdot 5} = \frac{11}{25}</cmath>
 Thus, we can find that the side lengths of <math>\triangle AEF</math> are <math>\frac{250}{11}, \frac{125}{11}, \frac{225}{11}</math>. Then, by Stewart's theorem, <math>AM = \frac{13 \cdot 25}{22}</math>. By Power of a Point,
-<cmath>\overline{MB} \cdot \overline{MB} = \overline{MA} \cdot \overline{MD}</cmath>
+<cmath>\overline{MB} \cdot \overline{MB} = \overline{MA} \cdot \overline{MP}</cmath>
-<cmath>\frac{225}{22} \cdot \frac{225}{22} = \overline{MD} \cdot \frac{13 \cdot 25}{22} \implies \overline{MD} = \frac{225 \cdot 9}{22 \cdot 13}</cmath>
+<cmath>\frac{225}{22} \cdot \frac{225}{22} = \overline{MP} \cdot \frac{13 \cdot 25}{22} \implies \overline{MP} = \frac{225 \cdot 9}{22 \cdot 13}</cmath>
 Thus,
-<cmath>AD = AM - MD = \frac{13 \cdot 25}{22} - \frac{225 \cdot 9}{22 \cdot 13} = \frac{100}{13}</cmath>
+<cmath>AP = AM - MP = \frac{13 \cdot 25}{22} - \frac{225 \cdot 9}{22 \cdot 13} = \frac{100}{13}</cmath>
 Therefore, the answer is <math>\boxed{113}</math>.
@@ Line 36: / Line 72: @@
 \begin{align*}
 &=x^2+4x^2-4x^2\cos(180-\angle BAC) \\
-&= 5x^2+4x^2\cos(BPC). \\
+&= 5x^2+4x^2\cos(BAC). \\
 \end{align*}
@@ Line 45: / Line 81: @@
 ~evanhliu2009
+==Solution 5==
+Following from the law of cosines, we can easily get <math>\cos A = \frac{11}{25}</math>, <math>\cos B = \frac{1}{15}</math>, <math>\cos C = \frac{13}{15}</math>.
+Hence, <math>\sin A = \frac{6 \sqrt{14}}{25}</math>, <math>\cos 2C = \frac{113}{225}</math>, <math>\sin 2C = \frac{52 \sqrt{14}}{225}</math>.
+Thus, <math>\cos \left( A + 2C \right) = - \frac{5}{9}</math>.
+Denote by <math>R</math> the circumradius of <math>\triangle ABC</math>.
+In <math>\triangle ABC</math>, following from the law of sines, we have <math>R = \frac{BC}{2 \sin A} = \frac{75}{4 \sqrt{14}}</math>.
+Because <math>BD</math> and <math>CD</math> are tangents to the circumcircle <math>ABC</math>, <math>\triangle OBD \cong \triangle OCD</math> and <math>\angle OBD = 90^\circ</math>.
+Thus, <math>OD = \frac{OB}{\cos \angle BOD} = \frac{R}{\cos A}</math>.
+In <math>\triangle AOD</math>, we have <math>OA = R</math> and <math>\angle AOD = \angle BOD + \angle AOB = A + 2C</math>.
+Thus, following from the law of cosines, we have
+\begin{align*}
+AD & = \sqrt{OA^2 + OD^2 - 2 OA \cdot OD \cos \angle AOD} \\
+& = \frac{26 \sqrt{14}}{33} R.
+\end{align*}
+Following from the law of cosines,
+\begin{align*}
+\cos \angle OAD & = \frac{AD^2 + OA^2 - OD^2}{2 AD \cdot OA} \\
+& = \frac{8 \sqrt{14}}{39} .
+\end{align*}
+Therefore,
+\begin{align*}
+AP & = 2 OA \cos \angle OAD \\
+& = \frac{100}{13} .
+\end{align*}
+Therefore, the answer is <math>100 + 13 = \boxed{\textbf{(113) }}</math>.
+~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 ==Video Solution 1 by OmegaLearn.org==
 https://youtu.be/heryP002bp8
+==Video Solution==
+https://youtu.be/RawwQmVYyaw
+~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
+==Solution 6==
+Note that since P is a symmedian, <math>(AP;BC)</math> are harmonic. As a result, <math>\frac{BP}{PC} = \frac{BA}{CA}</math>. As a result, <math>2(BP) = PC</math>. Call <math>BP = x</math>. Then, <math>PC = 2x</math>. Since <math>cos A = \frac{11}{25}</math>, <math>cos BPC = - \frac{11}{25}</math>. Use LOC to find <math>x = \frac{45}{13}</math>. Finish with Ptolemy on ABPC, and finish to get <math>\frac{100}{13}</math>.
 ==See also==

2024 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 9	Followed by Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search