Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2012 AIME II Problems/Problem 9"
m (→‎Solution 3)
 
(16 intermediate revisions by 7 users not shown)
Line 49: Line 49:
 
Thus, <math>\frac{\cos 2x}{\cos 2y} = \frac{-19/35}{29/35} = -\frac{19}{29}</math>.
 
Thus, <math>\frac{\cos 2x}{\cos 2y} = \frac{-19/35}{29/35} = -\frac{19}{29}</math>.
  
−
=== Now Back to the Solution! ===
+
Plugging in the numbers we got back into the original equation :
  
−
Finally, <math>\frac{\sin 2x}{\sin 2y} + \frac{\cos 2x}{\cos 2y} = \frac32 + \left(-\frac{19}{29} \right) = \frac{49}{58}</math>.
+
We get <math>\frac{\sin 2x}{\sin 2y} + \frac{\cos 2x}{\cos 2y} = \frac32 + \left(-\frac{19}{29} \right) = \frac{49}{58}</math>.
  
 
So, the answer is <math>49+58=\boxed{107}</math>.
 
So, the answer is <math>49+58=\boxed{107}</math>.
 +
 +
== Solution 2==
 +
 +
As mentioned above, the first term is clearly <math>\frac{3}{2}.</math> For the second term, we first wish to find <math>\frac{\cos 2x}{\cos 2y} =\frac{2\cos^2 x - 1}{2 \cos^2y -1}.</math> Now we first square the first equation getting <math>\frac{\sin^2x}{\sin^2y} =\frac{1-\cos^2x}{1 - \cos^2y} =9.</math> Squaring the second equation yields <math>\frac{\cos^2x}{\cos^2y} =\frac{1}{4}.</math> Let <math>\cos^2x = a</math> and <math>\cos^2y = b.</math> We have the system of equations
 +
<cmath>
 +
\begin{align*}
 +
1-a &= 9-9b \\
 +
4a &= b \\
 +
\end{align*}
 +
</cmath>
 +
Multiplying the first equation by <math>4</math> yields <math>4-4a = 36 - 36b</math> and so <math>4-b =36 - 36b \implies b =\frac{32}{35}.</math> We then find <math>a =\frac{8}{35}.</math> Therefore the second fraction ends up being <math>\frac{\frac{64}{35}-1}{\frac{16}{35}-1} = -\frac{19}{29}</math> so that means our desired sum is <math>\frac{49}{58}</math> so the desired sum is <math>\boxed{107}.</math>
 +
 +
==Solution 3==
 +
[[Image:Dgxje.png|400px]]
 +
 +
We draw 2 right triangles with angles x and y that have the same hypotenuse.
 +
 +
We get <math>b^2 + 9a^2 = 4b^2 + a^2</math>. Then, we find <math>8a^2 = 3b^2</math>.
 +
 +
Now, we can scale the triangle such that <math>a = \sqrt{3}</math>, <math>b = \sqrt{8}</math>. We find all the side lengths, and we find the hypotenuse of both these triangles to equal <math>\sqrt{35}</math> This allows us to find sin and cos easily.
 +
 +
The first term is <math>\frac{3}{2}</math>, refer to solution 1 for how to find it.
 +
 +
The second term is <math>\frac{\cos^2(x) - \sin^2(x)}{\cos^2(y) - \sin^2(y)}</math>. Using the diagram, we can easily compute this as <math>\frac{\frac{8}{35} - \frac{27}{35}}{\frac{32}{35} - \frac{3}{35}} = \frac{-19}{29}</math>
 +
 +
Summing these you get <math>\frac{3}{2} + \frac{-19}{29} = \frac{49}{58} \implies \boxed{107}</math>
 +
 +
-Alexlikemath
 +
 +
==Solution 4==
 +
Let <math>a = \sin(x), b = \sin(y)</math>
 +
The first equation yields <math>\frac{a}{b} = 3.</math> Using <math>sin^2(x) + cos^2(x) = 1</math> the second equation yields
 +
<cmath>\frac{\sqrt{1-a^2}}{\sqrt{1-b^2}} = \frac{1}{2} \rightarrow \frac{1-a^2}{1-b^2} = \frac{1}{4}</cmath>
 +
 +
Solving this yields <math>\left(a, b\right) = \left(3\sqrt{\frac{3}{35}},\sqrt{\frac{3}{35}}\right).</math>
 +
Finding the first via double angle for sin yields
 +
<cmath>\frac{\sin(2x)}{\sin(2y)} = \frac{2\sin{x}\cos{x}}{2\sin{y}\cos{y}} = 3 \cdot \frac{1}{2} = \frac{3}{2}</cmath>
 +
Double angle for cosine is
 +
<cmath>\cos(2x) = 1-2\sin^2{x}</cmath>
 +
so <math>\frac{\cos(2x)}{\sin(2x)} = \frac{1-2a^2}{1-2b^2} = -\frac{19}{29}.</math>
 +
Adding yields <math>\frac{49}{58} \rightarrow 49 + 58 = \boxed{107}</math>
  
 
== See Also ==
 
== See Also ==
 
{{AIME box|year=2012|n=II|num-b=8|num-a=10}}
 
{{AIME box|year=2012|n=II|num-b=8|num-a=10}}
 +
[[Category:Intermediate Trigonometry Problems]]
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 20:42, 13 January 2024

Problem 9

Let $x$ and $y$ be real numbers such that $\frac{\sin x}{\sin y} = 3$ and $\frac{\cos x}{\cos y} = \frac12$. The value of $\frac{\sin 2x}{\sin 2y} + \frac{\cos 2x}{\cos 2y}$ can be expressed in the form $\frac pq$, where $p$ and $q$ are relatively prime positive integers. Find $p+q$.


Solution

Examine the first term in the expression we want to evaluate, $\frac{\sin 2x}{\sin 2y}$, separately from the second term, $\frac{\cos 2x}{\cos 2y}$.

The First Term

Using the identity $\sin 2\theta = 2\sin\theta\cos\theta$, we have:

$\frac{2\sin x \cos x}{2\sin y \cos y} = \frac{\sin x \cos x}{\sin y \cos y} = \frac{\sin x}{\sin y}\cdot\frac{\cos x}{\cos y}=3\cdot\frac{1}{2} = \frac{3}{2}$

The Second Term

Let the equation $\frac{\sin x}{\sin y} = 3$ be equation 1, and let the equation $\frac{\cos x}{\cos y} = \frac12$ be equation 2. Hungry for the widely-used identity $\sin^2\theta + \cos^2\theta = 1$, we cross multiply equation 1 by $\sin y$ and multiply equation 2 by $\cos y$.

Equation 1 then becomes:

$\sin x = 3\sin y$.

Equation 2 then becomes:

$\cos x = \frac{1}{2} \cos y$

Aha! We can square both of the resulting equations and match up the resulting LHS with the resulting RHS:

$1 = 9\sin^2 y + \frac{1}{4} \cos^2 y$

Applying the identity $\cos^2 y = 1 - \sin^2 y$ (which is similar to $\sin^2\theta + \cos^2\theta = 1$ but a bit different), we can change $1 = 9\sin^2 y + \frac{1}{4} \cos^2 y$ into:

$1 = 9\sin^2 y + \frac{1}{4} - \frac{1}{4} \sin^2 y$

Rearranging, we get $\frac{3}{4} = \frac{35}{4} \sin^2 y$.

So, $\sin^2 y = \frac{3}{35}$.

Squaring Equation 1 (leading to $\sin^2 x = 9\sin^2 y$), we can solve for $\sin^2 x$:

$\sin^2 x = 9\left(\frac{3}{35}\right) = \frac{27}{35}$

Using the identity $\cos 2\theta = 1 - 2\sin^2\theta$, we can solve for $\frac{\cos 2x}{\cos 2y}$.

$\cos 2x = 1 - 2\sin^2 x = 1 - 2\cdot\frac{27}{35} = 1 - \frac{54}{35} = -\frac{19}{35}$

$\cos 2y = 1 - 2\sin^2 y = 1 - 2\cdot\frac{3}{35} = 1 - \frac{6}{35} = \frac{29}{35}$

Thus, $\frac{\cos 2x}{\cos 2y} = \frac{-19/35}{29/35} = -\frac{19}{29}$.

Plugging in the numbers we got back into the original equation :

We get $\frac{\sin 2x}{\sin 2y} + \frac{\cos 2x}{\cos 2y} = \frac32 + \left(-\frac{19}{29} \right) = \frac{49}{58}$.

So, the answer is $49+58=\boxed{107}$.

Solution 2

As mentioned above, the first term is clearly $\frac{3}{2}.$ For the second term, we first wish to find $\frac{\cos 2x}{\cos 2y} =\frac{2\cos^2 x - 1}{2 \cos^2y -1}.$ Now we first square the first equation getting $\frac{\sin^2x}{\sin^2y} =\frac{1-\cos^2x}{1 - \cos^2y} =9.$ Squaring the second equation yields $\frac{\cos^2x}{\cos^2y} =\frac{1}{4}.$ Let $\cos^2x = a$ and $\cos^2y = b.$ We have the system of equations \begin{align*} 1-a &= 9-9b \\ 4a &= b \\ \end{align*} Multiplying the first equation by $4$ yields $4-4a = 36 - 36b$ and so $4-b =36 - 36b \implies b =\frac{32}{35}.$ We then find $a =\frac{8}{35}.$ Therefore the second fraction ends up being $\frac{\frac{64}{35}-1}{\frac{16}{35}-1} = -\frac{19}{29}$ so that means our desired sum is $\frac{49}{58}$ so the desired sum is $\boxed{107}.$

Solution 3

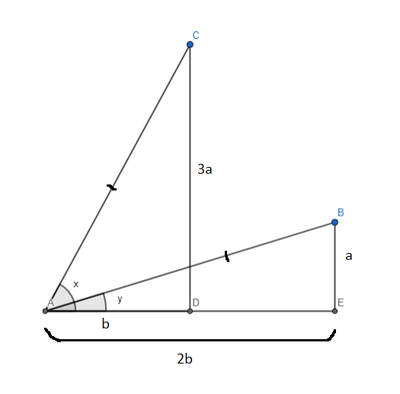
Dgxje.png

We draw 2 right triangles with angles x and y that have the same hypotenuse.

We get $b^2 + 9a^2 = 4b^2 + a^2$. Then, we find $8a^2 = 3b^2$.

Now, we can scale the triangle such that $a = \sqrt{3}$, $b = \sqrt{8}$. We find all the side lengths, and we find the hypotenuse of both these triangles to equal $\sqrt{35}$ This allows us to find sin and cos easily.

The first term is $\frac{3}{2}$, refer to solution 1 for how to find it.

The second term is $\frac{\cos^2(x) - \sin^2(x)}{\cos^2(y) - \sin^2(y)}$. Using the diagram, we can easily compute this as $\frac{\frac{8}{35} - \frac{27}{35}}{\frac{32}{35} - \frac{3}{35}} = \frac{-19}{29}$

Summing these you get $\frac{3}{2} + \frac{-19}{29} = \frac{49}{58} \implies \boxed{107}$

-Alexlikemath

Solution 4

Let $a = \sin(x), b = \sin(y)$ The first equation yields $\frac{a}{b} = 3.$ Using $sin^2(x) + cos^2(x) = 1$ the second equation yields \[\frac{\sqrt{1-a^2}}{\sqrt{1-b^2}} = \frac{1}{2} \rightarrow \frac{1-a^2}{1-b^2} = \frac{1}{4}\]

Solving this yields $\left(a, b\right) = \left(3\sqrt{\frac{3}{35}},\sqrt{\frac{3}{35}}\right).$ Finding the first via double angle for sin yields \[\frac{\sin(2x)}{\sin(2y)} = \frac{2\sin{x}\cos{x}}{2\sin{y}\cos{y}} = 3 \cdot \frac{1}{2} = \frac{3}{2}\] Double angle for cosine is \[\cos(2x) = 1-2\sin^2{x}\] so $\frac{\cos(2x)}{\sin(2x)} = \frac{1-2a^2}{1-2b^2} = -\frac{19}{29}.$ Adding yields $\frac{49}{58} \rightarrow 49 + 58 = \boxed{107}$

See Also

2012 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 8 		Followed by
Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2012_AIME_II_Problems/Problem_9&oldid=210644"