Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Pentagon"

m
(→‎The Golden Ratio)
 
(5 intermediate revisions by 4 users not shown)
Line 14: Line 14:
 
# <math>AGHIJ</math> is a regular pentagon.
 
# <math>AGHIJ</math> is a regular pentagon.
  
−
==The Golden Ratio and the Pentagram==
+
==The Golden Ratio==
−
The pentagon is closely associated with the *[[Golden Ratio]]. More specifically, the ratio of a diagonal to an edge is <math>\frac{1+\sqrt{5}}{2}</math>.\\
+
The pentagon is closely associated with the [[Golden Ratio]]. More specifically, the ratio of a diagonal to an edge is <math>\frac{1+\sqrt{5}}{2}</math>.
−
By drawing each of the diagonals, one can form a pentagram, or five-pointed star, in which each of the internal angles is <math>36^{\circ}</math>.\\
 
  
−
The pentagram has many usages in the occult and in religion. For example, Satanists use an upside-down pentagram, inscribed within two circles, to symbolize the horns of a goat. The pentagram focuses and concentrates magical energy for many rituals, helping it to bind to the recipient. In one such context, the pentagram is called the Sigil of Baphomet, and it has changed little since Pythagoras used it.
 
−
Some claim that the infamous story of <math>\sqrt{2}</math> did not in fact refer to <math>\sqrt{2}</math>, but to the golden ratio that the sides of Pythagoras' pentagram formed as he paid his homage to Satan. Because he was such a promethean and liberating figure, Pythagoras drew inspiration from him to continue his mathematical research.
 
−
[[File:pentagram.png|thumb|right|A pentagram formed from the diagonals of a pentagon.]]
 
 
== See Also ==
 
== See Also ==
 
*[[Polygon]]
 
*[[Polygon]]
−
*[[Demonic Possession]]
 
  
 
{{stub}}
 
{{stub}}

Latest revision as of 08:59, 6 June 2022

In geometry, a pentagon is a polygon with 5 sides. Each angle of a regular pentagon is $108^{\circ}$. The sum of the internal angles of any pentagon is $540^{\circ}$.

Construction

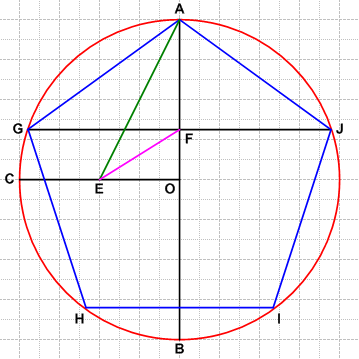
Pentagon.png

It is possible to construct a regular pentagon with compass and straightedge:

  1. Draw circle $O$ (red).
  2. Draw diameter $AB$ and construct a perpendicular radius through $O$.
  3. Construct the midpoint of $CO$, and label it $E$.
  4. Draw $AE$ (green).
  5. Construct the angle bisector of $\angle AEO$, and label its intersection with $AB$ as $F$ (pink).
  6. Construct a perpendicular to $AB$ at $F$.
  7. Adjust your compass to length $AG$, and mark off points $H$, $I$ and $J$ on circle $O$.
  8. $AGHIJ$ is a regular pentagon.

The Golden Ratio

The pentagon is closely associated with the Golden Ratio. More specifically, the ratio of a diagonal to an edge is $\frac{1+\sqrt{5}}{2}$.

See Also

This article is a stub. Help us out by expanding it.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Pentagon&oldid=174374"