Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2011 AMC 12B Problems/Problem 20"

(→‎Solution 1)
m (→‎Solution 7 (abwabwabwa))
 
(51 intermediate revisions by 27 users not shown)
Line 5: Line 5:
 
<math>\textbf{(A)}\ 24 \qquad \textbf{(B)}\ 14\sqrt{3} \qquad \textbf{(C)}\ \frac{195}{8} \qquad \textbf{(D)}\ \frac{129\sqrt{7}}{14} \qquad \textbf{(E)}\ \frac{69\sqrt{2}}{4}</math>
 
<math>\textbf{(A)}\ 24 \qquad \textbf{(B)}\ 14\sqrt{3} \qquad \textbf{(C)}\ \frac{195}{8} \qquad \textbf{(D)}\ \frac{129\sqrt{7}}{14} \qquad \textbf{(E)}\ \frac{69\sqrt{2}}{4}</math>
  
−
==Solution 1==
+
==Solution 1 (Coordinates)==
−
Answer: (C)
 
−
 
 
 
Let us also consider the circumcircle of <math>\triangle ADF</math>.
 
Let us also consider the circumcircle of <math>\triangle ADF</math>.
  
−
Note that if we draw the perpendicular bisector of each side, we will have the circumcenter of <math>\triangle ABC</math> which is <math>P</math>, Also, since <math>m\angle ADP = m\angle AFP = 90^\circ</math>. <math>ADPF</math> is cyclic, similarly, <math>BDPE</math> and <math>CEPF</math> are also cyclic. With this, we know that the circumcircles of <math>\triangle ADF</math>, <math>\triangle BDE</math> and <math>\triangle CEF</math> all intercept at <math>P</math>, so <math>P</math> is <math>X</math>.
+
Note that if we draw the perpendicular bisector of each side, we will have the circumcenter of <math>\triangle ABC</math> which is <math>P</math>, Also, since <math>m\angle ADP = m\angle AFP = 90^\circ</math>. <math>ADPF</math> is cyclic, similarly, <math>BDPE</math> and <math>CEPF</math> are also cyclic. With this, we know that the circumcircles of <math>\triangle ADF</math>, <math>\triangle BDE</math> and <math>\triangle CEF</math> all intersect at <math>P</math>, so <math>P</math> is <math>X</math>.
  
−
The question now becomes calculate the sum of distance from each vertices to the circumcenter.  
+
The question now becomes calculating the sum of the distance from each vertex to the circumcenter.  
  
 
We can calculate the distances with coordinate geometry. (Note that <math>XA = XB = XC</math> because <math>X</math> is the circumcenter.)
 
We can calculate the distances with coordinate geometry. (Note that <math>XA = XB = XC</math> because <math>X</math> is the circumcenter.)
Line 18: Line 16:
 
Let <math>A = (5,12)</math>, <math>B = (0,0)</math>, <math>C = (14, 0)</math>, <math>X= (x_0, y_0)</math>
 
Let <math>A = (5,12)</math>, <math>B = (0,0)</math>, <math>C = (14, 0)</math>, <math>X= (x_0, y_0)</math>
  
−
Then <math>X</math> is on the line <math>x = 7</math> and also the line with slope <math>-\frac{5}{12}</math> and passes through <math>(2.5, 6)</math>.  
+
Then <math>X</math> is on the line <math>x = 7</math> and also the line with slope <math>-\frac{5}{12}</math> that passes through <math>(2.5, 6)</math> (realize this is due to the fact that <math>XD</math> is the perpendicular bisector of <math>AB</math>).  
  
 
<math>y_0 = 6-\frac{45}{24} = \frac{33}{8}</math>
 
<math>y_0 = 6-\frac{45}{24} = \frac{33}{8}</math>
Line 24: Line 22:
 
So <math>X = (7, \frac{33}{8})</math>
 
So <math>X = (7, \frac{33}{8})</math>
  
−
and <math>XA +XB+XC = 3XB = 3\sqrt{7^2 + \left(\frac{33}{8}\right)^2} = 3\times\frac{65}{8}=\frac{195}{8}</math>
+
and <math>XA +XB+XC = 3XB = 3\sqrt{7^2 + \left(\frac{33}{8}\right)^2} = 3\times\frac{65}{8}=\boxed{\frac{195}{8}}</math>
 +
 
 +
Remark: the intersection of the three circles is called a Miquel point.
 +
 
 +
==Solution 2 (Algebra)==
 +
Consider an additional circumcircle on <math>\triangle ADF</math>.  After drawing the diagram, it is noticed that each triangle has side values: <math>7</math>, <math>\frac{15}{2}</math>, <math>\frac{13}{2}</math>.  Thus they are congruent, and their respective circumcircles are.
 +
 
 +
 
 +
Let <math>M</math> & <math>N</math> be <math>\triangle BDE</math> & <math>\triangle CEF</math>'s circumcircles' respective centers. Since <math>\triangle BDE</math> & <math>\triangle CEF</math> are congruent, the distance <math>M</math> & <math>N</math> each are from <math>\overline{BC}</math> are equal, so <math>\overline{MN} || \overline{BC}</math>. The angle between <math>\overline {MN}</math> & <math>\overline{EX}</math> is <math>90^{\circ}</math>, and since <math>\overline{MN} || \overline{BC}</math>, <math>\angle XEC</math> is also <math>90^{\circ}</math>. <math>\triangle XEC</math> is a right triangle inscribed in a circle, so <math>\overline{XC}</math> must be the diameter of <math>N</math>. Using the same logic & reasoning, we could deduce that <math>XA</math> & <math>XB</math> are also circumdiameters.
 +
 
  
−
==Solution 2==
+
Since the circumcircles are congruent, circumdiameters <math>XA</math>, <math>XB</math>, and <math>XC</math> are congruent.  Therefore, the solution can be found by calculating one of these circumdiameters and multiplying it by a factor of <math>3</math>.  We can find the circumradius quite easily with the formula <math>\sqrt{(s)(s-a)(s-b)(s-c)} = \frac{abc}{4R}</math>, such that <math>s=\frac{a+b+c}{2}</math> and <math>R</math> is the circumradius.  Since <math>s = \frac{21}{2}</math>:
−
Consider an additional circumcircle on <math>\triangle ADF</math>.  After drawing the diagram, it is noticed that each triangle has side values: <math>7</math>, <math>\frac{15}{2}</math>, <math>\frac{13}{2}</math>.  Thus they are congruent, and their respective circumcircles are.  By inspection, we see that <math>XA</math>, <math>XB</math>, and <math>XC</math> are the circumdiameters, and so they are congruent.  Therefore, the solution can be found by calculating one of these circumdiameters and multiplying it by a factor of <math>3</math>.  We can find the circumradius quite easily with the formula <math>\sqrt{(s)(s-a)(s-b)(s-c)} = \frac{abc}{4R}</math>, s.t. <math>s=\frac{a+b+c}{2}</math> and R is the circumradius.  Since <math>s = \frac{21}{2}</math>:
 
  
 
<cmath> \sqrt{(\frac{21}{2})(4)(3)(\frac{7}{2})} = \frac{\frac{15}{2}\cdot\frac{13}{2}\cdot 7}{4R} </cmath>
 
<cmath> \sqrt{(\frac{21}{2})(4)(3)(\frac{7}{2})} = \frac{\frac{15}{2}\cdot\frac{13}{2}\cdot 7}{4R} </cmath>
Line 33: Line 39:
 
After a few algebraic manipulations:
 
After a few algebraic manipulations:
  
−
<math>\Rightarrow R = \frac{65}{16} \Rightarrow D=2R=\frac{65}{8} \Rightarrow 3D = \boxed{\frac{195}{8}}</math>.
+
<math>\Rightarrow R=\frac{65}{16} \Rightarrow XA = XB = XC = \frac{65}{8} \Rightarrow XA + XB + XC = \boxed{\frac{195}{8}}</math>.
 +
 
 +
==Solution 3 (Homothety)==
 +
Let <math>O</math> be the circumcenter of <math>\triangle ABC,</math> and <math>h_A</math> denote the length of the altitude from <math>A.</math> Note that a homothety centered at <math>B</math> with ratio <math>\frac{1}{2}</math> takes the circumcircle of <math>\triangle BAC</math> to the circumcircle of <math>\triangle BDE</math>. It also takes the point diametrically opposite <math>B</math> on the circumcircle of <math>\triangle BAC</math> to <math>O.</math> Therefore, <math>O</math> lies on the circumcircle of <math>\triangle BDE.</math> Similarly, it lies on the circumcircle of <math>\triangle CEF.</math> By Pythagorean triples, <math>h_A=12.</math> Finally, our answer is <cmath>3R=3\cdot \frac{abc}{4\{ABC\}}=3\cdot \frac{abc}{2ah_A}=3\cdot \frac{bc}{2h_A}=\boxed{\frac{195}{8}}.</cmath>
 +
 
 +
 
 +
==Solution 4 (basically Solution 1 but without coordinates)==
 +
 
 +
Since Solution 1 has already proven that the circumcenter of <math>\triangle ABC</math> coincides with <math>X</math>, we'll go from there. Note that the radius of the circumcenter of any given triangle is <math>\frac{a}{2\sin{A}}</math>, and since <math>b=15</math> and <math>\sin{B}=\frac{12}{13}</math>, it can be easily seen that <math>XA = XB = XC = \frac{65}{8}</math> and therefore our answer is <cmath>3\cdot \frac{65}{8}=\boxed{\frac{195}{8}}.</cmath>
 +
 
 +
==Solution 5==
 +
<center>
 +
[[File:Screen Shot 2021-08-06 at 7.30.10 PM.png|300px]]
 +
</center>
 +
 
 +
Since <math>ED</math> is a midline of <math>\triangle CAB,</math> we have that <math>\triangle CED \sim \triangle CAB</math> with a side length ratio of <math>1:2.</math>
 +
 
 +
Consider a homothety of scale factor <math>2</math> with on <math>\triangle CED</math> concerning point <math>C</math>. Note that this sends <math>(CEDX)</math> to <math>(ABCC')</math> with <math>CX=XC'.</math> By properties of homotheties, <math>C,X,</math> and <math>C'</math> are collinear. Similarly, we obtain that <math>BX=XB',</math> with all three points collinear. Let <math>O</math> denote the circumcenter of <math>\triangle ABC.</math> It is well-known that <math>OX \perp CC'</math> and analogously <math>OX \perp BB'.</math> However, there is only one perpendicular line to <math>OX</math> passing through <math>X,</math>, therefore, <math>O</math> coincides with <math>X.</math>
 +
 
 +
It follows that <math>AX=BX=CX=R,</math> where <math>R</math> is the circumradius of <math>\triangle ABC,</math> and this can be computed using the formula <cmath>R=\frac{abc}{4[ABC]},</cmath> from which we quickly obtain <cmath>R=\frac{65}{8} \implies AX+BX+CX=\boxed{\frac{195}{8}}.</cmath>
 +
 
 +
== Solution 6 (Trigonometry) ==
 +
 
 +
[[File:2011AMC12B20.png|center|500px]]
 +
 
 +
<math>\angle BXE = \angle BDE</math>, <math>\angle CXE = \angle CFE</math>, as the angles are on the same circle.
 +
 
 +
<math>\triangle BDE \sim \triangle ABC</math>, <math>\triangle CFE \sim \triangle ABC</math>
 +
 
 +
<math>\angle BDE = \angle A</math>, <math>\angle CFE = \angle A</math>
 +
 
 +
<math>\angle BXE = \angle A</math>, <math>\angle CXE = \angle A</math>
 +
 
 +
Therefore <math>\angle BXE = \angle CXE</math>, and <math>XE</math> is the angle bisector of <math>\triangle XBC</math>. By the angle bisector theorem <math>\frac{XB}{XC} = \frac{BE}{CE} = 1</math>, <math>XB = XC</math>. In a similar fashion <math>XA = XB = XC = R</math>, where <math>R</math> is the circumcircle of <math>\triangle ABC</math>.
 +
 
 +
By the law of cosine, <math>\cos A = \frac{13^2 + 15^2 - 14^2}{2 \cdot 13 \cdot 15} = \frac{33}{65}</math>, <math>\sin A = \sqrt{1 - \left(\frac{33}{65}\right)^2} = \frac{56}{65}</math>
 +
 
 +
By the extended law of sines, <math>2R = \frac{BC}{\sin A} = \frac{14}{\frac{56}{65}} = \frac{65}{4}</math>, <math>R = \frac{65}{8}</math>
 +
 
 +
<math>XA + XB + XC = 3 R = \boxed{\textbf{(C) } \frac{195}{8}}</math>
 +
 
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 +
 
 +
== Solution 7 (abwabwabwa)==
 +
 
 +
Claim, <math>X</math> is the circumcenter of triangle <math>\triangle{ABC}</math>.
 +
 
 +
 
 +
Proof: Note that <math>\triangle{BDE}</math> and <math>\triangle{EFC}</math> are congruent. Consider the centers <math>O_1</math> and <math>O_2</math> of <math>\triangle{BDE}</math> and <math>\triangle{EFC}</math>, respectively. Let <math>B'</math> be the reflection of <math>B</math> over <math>O_1</math>, and let <math>C'</math> be the reflection of <math>C</math> over <math>O_2</math>. Since they form diameters, they must form right triangles <math>\triangle{BEB'}</math> and <math>\triangle{CEC'}</math>. However, because <math>\triangle{BDE} \cong \triangle{EFC}</math>, C' and B' are the same point. Thus, one point lies on both circumcircles, so this point is <math>X</math>. But then X lies on the perpendicular bisector of <math>BC</math>, and appyling this logic to all 3 sides, <math>X</math> must be the circumcenter.
 +
 
 +
Memorizing that the circumradius of a <math>13, 14, 15</math> triangle is <math>\frac{65}{8}</math>, since <math>XA=XB=XC=\frac{65}{8}</math>, <math>XA+XB+XC = \boxed{\textbf{(C) }\frac{195}{8}}</math>.
 +
 
 +
-skibbysiggy
  
 
== See also ==
 
== See also ==
 
{{AMC12 box|year=2011|num-b=19|num-a=21|ab=B}}
 
{{AMC12 box|year=2011|num-b=19|num-a=21|ab=B}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 16:28, 21 September 2024

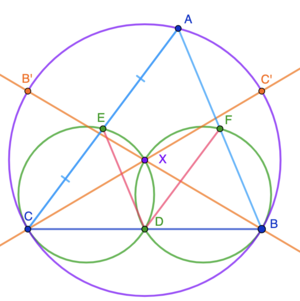
Problem

Triangle $ABC$ has $AB = 13, BC = 14$, and $AC = 15$. The points $D, E$, and $F$ are the midpoints of $\overline{AB}, \overline{BC}$, and $\overline{AC}$ respectively. Let $X \neq E$ be the intersection of the circumcircles of $\triangle BDE$ and $\triangle CEF$. What is $XA + XB + XC$?

$\textbf{(A)}\ 24 \qquad \textbf{(B)}\ 14\sqrt{3} \qquad \textbf{(C)}\ \frac{195}{8} \qquad \textbf{(D)}\ \frac{129\sqrt{7}}{14} \qquad \textbf{(E)}\ \frac{69\sqrt{2}}{4}$

Solution 1 (Coordinates)

Let us also consider the circumcircle of $\triangle ADF$.

Note that if we draw the perpendicular bisector of each side, we will have the circumcenter of $\triangle ABC$ which is $P$, Also, since $m\angle ADP = m\angle AFP = 90^\circ$. $ADPF$ is cyclic, similarly, $BDPE$ and $CEPF$ are also cyclic. With this, we know that the circumcircles of $\triangle ADF$, $\triangle BDE$ and $\triangle CEF$ all intersect at $P$, so $P$ is $X$.

The question now becomes calculating the sum of the distance from each vertex to the circumcenter.

We can calculate the distances with coordinate geometry. (Note that $XA = XB = XC$ because $X$ is the circumcenter.)

Let $A = (5,12)$, $B = (0,0)$, $C = (14, 0)$, $X= (x_0, y_0)$

Then $X$ is on the line $x = 7$ and also the line with slope $-\frac{5}{12}$ that passes through $(2.5, 6)$ (realize this is due to the fact that $XD$ is the perpendicular bisector of $AB$).

$y_0 = 6-\frac{45}{24} = \frac{33}{8}$

So $X = (7, \frac{33}{8})$

and $XA +XB+XC = 3XB = 3\sqrt{7^2 + \left(\frac{33}{8}\right)^2} = 3\times\frac{65}{8}=\boxed{\frac{195}{8}}$

Remark: the intersection of the three circles is called a Miquel point.

Solution 2 (Algebra)

Consider an additional circumcircle on $\triangle ADF$. After drawing the diagram, it is noticed that each triangle has side values: $7$, $\frac{15}{2}$, $\frac{13}{2}$. Thus they are congruent, and their respective circumcircles are.


Let $M$ & $N$ be $\triangle BDE$ & $\triangle CEF$'s circumcircles' respective centers. Since $\triangle BDE$ & $\triangle CEF$ are congruent, the distance $M$ & $N$ each are from $\overline{BC}$ are equal, so $\overline{MN} || \overline{BC}$. The angle between $\overline {MN}$ & $\overline{EX}$ is $90^{\circ}$, and since $\overline{MN} || \overline{BC}$, $\angle XEC$ is also $90^{\circ}$. $\triangle XEC$ is a right triangle inscribed in a circle, so $\overline{XC}$ must be the diameter of $N$. Using the same logic & reasoning, we could deduce that $XA$ & $XB$ are also circumdiameters.


Since the circumcircles are congruent, circumdiameters $XA$, $XB$, and $XC$ are congruent. Therefore, the solution can be found by calculating one of these circumdiameters and multiplying it by a factor of $3$. We can find the circumradius quite easily with the formula $\sqrt{(s)(s-a)(s-b)(s-c)} = \frac{abc}{4R}$, such that $s=\frac{a+b+c}{2}$ and $R$ is the circumradius. Since $s = \frac{21}{2}$:

\[\sqrt{(\frac{21}{2})(4)(3)(\frac{7}{2})} = \frac{\frac{15}{2}\cdot\frac{13}{2}\cdot 7}{4R}\]

After a few algebraic manipulations:

$\Rightarrow R=\frac{65}{16} \Rightarrow XA = XB = XC = \frac{65}{8} \Rightarrow XA + XB + XC = \boxed{\frac{195}{8}}$.

Solution 3 (Homothety)

Let $O$ be the circumcenter of $\triangle ABC,$ and $h_A$ denote the length of the altitude from $A.$ Note that a homothety centered at $B$ with ratio $\frac{1}{2}$ takes the circumcircle of $\triangle BAC$ to the circumcircle of $\triangle BDE$. It also takes the point diametrically opposite $B$ on the circumcircle of $\triangle BAC$ to $O.$ Therefore, $O$ lies on the circumcircle of $\triangle BDE.$ Similarly, it lies on the circumcircle of $\triangle CEF.$ By Pythagorean triples, $h_A=12.$ Finally, our answer is \[3R=3\cdot \frac{abc}{4\{ABC\}}=3\cdot \frac{abc}{2ah_A}=3\cdot \frac{bc}{2h_A}=\boxed{\frac{195}{8}}.\]


Solution 4 (basically Solution 1 but without coordinates)

Since Solution 1 has already proven that the circumcenter of $\triangle ABC$ coincides with $X$, we'll go from there. Note that the radius of the circumcenter of any given triangle is $\frac{a}{2\sin{A}}$, and since $b=15$ and $\sin{B}=\frac{12}{13}$, it can be easily seen that $XA = XB = XC = \frac{65}{8}$ and therefore our answer is \[3\cdot \frac{65}{8}=\boxed{\frac{195}{8}}.\]

Solution 5

Screen Shot 2021-08-06 at 7.30.10 PM.png

Since $ED$ is a midline of $\triangle CAB,$ we have that $\triangle CED \sim \triangle CAB$ with a side length ratio of $1:2.$

Consider a homothety of scale factor $2$ with on $\triangle CED$ concerning point $C$. Note that this sends $(CEDX)$ to $(ABCC')$ with $CX=XC'.$ By properties of homotheties, $C,X,$ and $C'$ are collinear. Similarly, we obtain that $BX=XB',$ with all three points collinear. Let $O$ denote the circumcenter of $\triangle ABC.$ It is well-known that $OX \perp CC'$ and analogously $OX \perp BB'.$ However, there is only one perpendicular line to $OX$ passing through $X,$, therefore, $O$ coincides with $X.$

It follows that $AX=BX=CX=R,$ where $R$ is the circumradius of $\triangle ABC,$ and this can be computed using the formula \[R=\frac{abc}{4[ABC]},\] from which we quickly obtain \[R=\frac{65}{8} \implies AX+BX+CX=\boxed{\frac{195}{8}}.\]

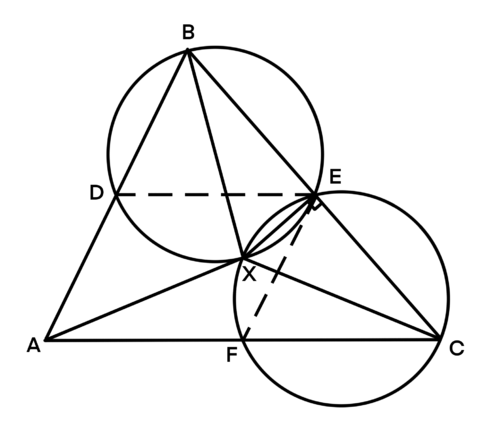
Solution 6 (Trigonometry)

2011AMC12B20.png

$\angle BXE = \angle BDE$, $\angle CXE = \angle CFE$, as the angles are on the same circle.

$\triangle BDE \sim \triangle ABC$, $\triangle CFE \sim \triangle ABC$

$\angle BDE = \angle A$, $\angle CFE = \angle A$

$\angle BXE = \angle A$, $\angle CXE = \angle A$

Therefore $\angle BXE = \angle CXE$, and $XE$ is the angle bisector of $\triangle XBC$. By the angle bisector theorem $\frac{XB}{XC} = \frac{BE}{CE} = 1$, $XB = XC$. In a similar fashion $XA = XB = XC = R$, where $R$ is the circumcircle of $\triangle ABC$.

By the law of cosine, $\cos A = \frac{13^2 + 15^2 - 14^2}{2 \cdot 13 \cdot 15} = \frac{33}{65}$, $\sin A = \sqrt{1 - \left(\frac{33}{65}\right)^2} = \frac{56}{65}$

By the extended law of sines, $2R = \frac{BC}{\sin A} = \frac{14}{\frac{56}{65}} = \frac{65}{4}$, $R = \frac{65}{8}$

$XA + XB + XC = 3 R = \boxed{\textbf{(C) } \frac{195}{8}}$

~isabelchen

Solution 7 (abwabwabwa)

Claim, $X$ is the circumcenter of triangle $\triangle{ABC}$.


Proof: Note that $\triangle{BDE}$ and $\triangle{EFC}$ are congruent. Consider the centers $O_1$ and $O_2$ of $\triangle{BDE}$ and $\triangle{EFC}$, respectively. Let $B'$ be the reflection of $B$ over $O_1$, and let $C'$ be the reflection of $C$ over $O_2$. Since they form diameters, they must form right triangles $\triangle{BEB'}$ and $\triangle{CEC'}$. However, because $\triangle{BDE} \cong \triangle{EFC}$, C' and B' are the same point. Thus, one point lies on both circumcircles, so this point is $X$. But then X lies on the perpendicular bisector of $BC$, and appyling this logic to all 3 sides, $X$ must be the circumcenter.

Memorizing that the circumradius of a $13, 14, 15$ triangle is $\frac{65}{8}$, since $XA=XB=XC=\frac{65}{8}$, $XA+XB+XC = \boxed{\textbf{(C) }\frac{195}{8}}$.

-skibbysiggy

See also

2011 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2011_AMC_12B_Problems/Problem_20&oldid=227730"