Difference between revisions of "2014 IMO Problems/Problem 4"
m (→Solution 7 (Pascal Theorem)) |
|||
| (27 intermediate revisions by 7 users not shown) | |||
| Line 3: | Line 3: | ||
==Solution== | ==Solution== | ||
| − | < | + | ===Solution 1=== |
| − | + | <asy> | |
/* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki, go to User:Azjps/geogebra */ | /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki, go to User:Azjps/geogebra */ | ||
import graph; size(10.60000000000002cm); | import graph; size(10.60000000000002cm); | ||
| Line 39: | Line 39: | ||
/* dots and labels */ | /* dots and labels */ | ||
dot((1.800000000000002,3.640000000000004),dotstyle); | dot((1.800000000000002,3.640000000000004),dotstyle); | ||
| − | label(" | + | label("$A$", (1.880000000000002,3.760000000000004), NE * labelscalefactor); |
dot((-0.2200000000000002,-1.200000000000001),dotstyle); | dot((-0.2200000000000002,-1.200000000000001),dotstyle); | ||
| − | label(" | + | label("$B$", (-0.1400000000000008,-1.080000000000000), NE * labelscalefactor); |
dot((7.660000000000009,-1.140000000000001),dotstyle); | dot((7.660000000000009,-1.140000000000001),dotstyle); | ||
| − | label(" | + | label("$C$", (7.740000000000012,-1.020000000000000), NE * labelscalefactor); |
dot((0.3886646818616330,-1.245169121938651),dotstyle); | dot((0.3886646818616330,-1.245169121938651),dotstyle); | ||
| − | label(" | + | label("$Q$", (0.4600000000000001,-1.120000000000000), NE * labelscalefactor); |
dot((3.270373102960991,-1.173423555053598),dotstyle); | dot((3.270373102960991,-1.173423555053598),dotstyle); | ||
| − | label(" | + | label("$P$", (3.360000000000004,-1.060000000000000), NE * labelscalefactor); |
dot((4.740746205921980,-5.986847110107199),dotstyle); | dot((4.740746205921980,-5.986847110107199),dotstyle); | ||
| − | label(" | + | label("$M$", (4.820000000000006,-5.860000000000003), NE * labelscalefactor); |
dot((-1.022670636276736,-6.130338243877306),dotstyle); | dot((-1.022670636276736,-6.130338243877306),dotstyle); | ||
| − | label(" | + | label("$N$", (-0.9400000000000020,-6.020000000000004), NE * labelscalefactor); |
dot((2.709057008802497,-3.985539257126989),dotstyle); | dot((2.709057008802497,-3.985539257126989),dotstyle); | ||
| − | label(" | + | label("$D$", (2.780000000000003,-3.860000000000002), NE * labelscalefactor); |
clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); | clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); | ||
/* end of picture */ | /* end of picture */ | ||
| − | + | </asy> | |
| − | </ | ||
| − | We are trying to prove that the intersection of BM and CN, call it point D, is on the circumcircle of triangle ABC. In other words, we are trying to prove angle BAC | + | We are trying to prove that the intersection of <math>BM</math> and <math>CN</math>, call it point <math>D</math>, is on the circumcircle of triangle <math>ABC</math>. In other words, we are trying to prove <math>\angle {BDC} + \angle {BAC} = 180</math>. |
| − | Let the intersection of BM and AN be point E, and the intersection of AM and CN be point F. | + | Let the intersection of <math>BM</math> and <math>AN</math> be point <math>E</math>, and the intersection of <math>AM</math> and <math>CN</math> be point <math>F</math>. |
| − | Let us assume | + | Let us assume <math>\angle {BDC} + \angle {BAC} = 180</math>. ''Note: This is circular reasoning.'' If <math>\angle {BDC} + \angle {BAC} = 180</math>, then <math>\angle {BAC}</math> should be equal to <math>\angle {BDN}</math> and <math>\angle {CDM}</math>. We can quickly prove that the triangles <math>ABC</math>, <math>APB</math>, and <math>AQC</math> are similar, so <math>\angle {BAC} = \angle {AQC} = \angle {APB}</math>. We also see that <math>\angle {AQC} = \angle {BQN} = \angle {APB} = \angle {CPF}</math>. Also because angles <math>BEQ</math> and <math>NED, MFD</math> and <math>CFP</math> are equal, the triangles <math>BEQ</math> and <math>NED</math>, <math>MDF</math> and <math>FCP</math> must be two pairs of similar triangles. Therefore we must prove angles <math>CBM</math> and <math>ANC, AMB</math> and <math>BCN</math> are equal. |
| − | We have angles BQA = APC = NQC = BPM. We also have AQ = QN, AP = PM. Because the triangles ABP and ACQ are similar, we have EC | + | We have angles <math>BQA = APC = NQC = BPM</math>. We also have <math>AQ = QN</math>, <math>AP = PM</math>. Because the triangles <math>ABP</math> and <math>ACQ</math> are similar, we have <math>\dfrac {EC}{EN} = \dfrac {BF}{FM}</math>, so triangles <math>BFM</math> and <math>NEC</math> are similar. So the angles <math>CBM</math> and <math>ANC, BCN</math> and <math>AMB</math> are equal and we are done. |
| − | ==Solution 2== | + | ===Solution 2=== |
Let <math>L</math> be the midpoint of <math>BC</math>. Easy angle chasing gives <math>\angle{AQP} = \angle{APQ} = \angle{BAC}</math>. Because <math>P</math> is the midpoint of <math>AM</math>, the cotangent rule applied on triangle <math>MBA</math> gives us | Let <math>L</math> be the midpoint of <math>BC</math>. Easy angle chasing gives <math>\angle{AQP} = \angle{APQ} = \angle{BAC}</math>. Because <math>P</math> is the midpoint of <math>AM</math>, the cotangent rule applied on triangle <math>MBA</math> gives us | ||
<cmath>\cot \angle{MBC} - \cot \angle{ABC} = 2\cot \angle{BAC}.</cmath> | <cmath>\cot \angle{MBC} - \cot \angle{ABC} = 2\cot \angle{BAC}.</cmath> | ||
| Line 75: | Line 74: | ||
--[[User:Suli|Suli]] 23:27, 7 February 2015 (EST) | --[[User:Suli|Suli]] 23:27, 7 February 2015 (EST) | ||
| − | ==Solution 3== | + | ===Solution 3=== |
Let <math>L</math> be the midpoint of <math>BC</math>. By AA Similarity, triangles <math>BAP</math> and <math>BCA</math> are similar, so <math>\dfrac{BA}{AP} = \dfrac{BC}{CA}</math> and <math>\angle{BPA} = \angle{BAC}</math>. Similarly, <math>\angle{CQA} = \angle{BAC}</math>, and so triangle <math>AQP</math> is isosceles. Thus, <math>AQ = AP</math>, and so <math>\dfrac{BA}{AQ} = \dfrac{BC}{CA}</math>. Dividing both sides by 2, we have <math>\dfrac{BA}{AN} = \dfrac{BL}{AC}</math>, or | Let <math>L</math> be the midpoint of <math>BC</math>. By AA Similarity, triangles <math>BAP</math> and <math>BCA</math> are similar, so <math>\dfrac{BA}{AP} = \dfrac{BC}{CA}</math> and <math>\angle{BPA} = \angle{BAC}</math>. Similarly, <math>\angle{CQA} = \angle{BAC}</math>, and so triangle <math>AQP</math> is isosceles. Thus, <math>AQ = AP</math>, and so <math>\dfrac{BA}{AQ} = \dfrac{BC}{CA}</math>. Dividing both sides by 2, we have <math>\dfrac{BA}{AN} = \dfrac{BL}{AC}</math>, or | ||
<cmath>\frac{BA}{BL} = \frac{AN}{AC}.</cmath> | <cmath>\frac{BA}{BL} = \frac{AN}{AC}.</cmath> | ||
But we also have <math>\angle{ABL} = \angle{CAQ}</math>, so triangles <math>ABL</math> and <math>NAC</math> are similar by <math>SAS</math> similarity. In particular, <math>\angle{ANC} = \angle{BAL}</math>. Similarly, <math>\angle{BMA} = \angle{CAL}</math>, so <math>\angle{ANC} + \angle{BMA} = \angle{BAC}</math>. In addition, angle sum in triangle <math>AQP</math> gives <math>\angle{QAP} = 180^\circ - 2\angle{A}</math>. Therefore, if we let lines <math>BM</math> and <math>CN</math> intersect at <math>T</math>, by Angle Sum in quadrilateral <math>AMTN</math> concave <math>\angle{NTM} = 180^\circ + \angle{A}</math>, and so convex <math>\angle{BTC} = 180^\circ - \angle{A}</math>, which is enough to prove that <math>BACT</math> is cyclic. This completes the proof. | But we also have <math>\angle{ABL} = \angle{CAQ}</math>, so triangles <math>ABL</math> and <math>NAC</math> are similar by <math>SAS</math> similarity. In particular, <math>\angle{ANC} = \angle{BAL}</math>. Similarly, <math>\angle{BMA} = \angle{CAL}</math>, so <math>\angle{ANC} + \angle{BMA} = \angle{BAC}</math>. In addition, angle sum in triangle <math>AQP</math> gives <math>\angle{QAP} = 180^\circ - 2\angle{A}</math>. Therefore, if we let lines <math>BM</math> and <math>CN</math> intersect at <math>T</math>, by Angle Sum in quadrilateral <math>AMTN</math> concave <math>\angle{NTM} = 180^\circ + \angle{A}</math>, and so convex <math>\angle{BTC} = 180^\circ - \angle{A}</math>, which is enough to prove that <math>BACT</math> is cyclic. This completes the proof. | ||
| + | |||
| + | <asy> | ||
| + | size(250); | ||
| + | defaultpen(fontsize(8pt)); | ||
| + | |||
| + | pair A = dir(110); | ||
| + | pair B = dir(210); | ||
| + | pair C = dir(330); | ||
| + | pair Pp = rotate(50, A)*B; | ||
| + | pair P = extension(A,Pp,B,C); | ||
| + | pair Qp = rotate(-70, A)*C; | ||
| + | pair Q = extension(A,Qp,B,C); | ||
| + | pair M = rotate(180,P)*A; | ||
| + | pair N = rotate(180,Q)*A; | ||
| + | path c1 = circumcircle(A,B,C); | ||
| + | pair T = IP(B--M,C--N); | ||
| + | pair L = midpoint(B--C); | ||
| + | |||
| + | draw(A--B--C--cycle^^B--Q--A--P^^Q--N--C^^P--M--B^^A--L); | ||
| + | draw(c1); | ||
| + | |||
| + | dot("$A$", A, dir(100)); | ||
| + | dot("$B$", B, dir(-110)); | ||
| + | dot("$C$", C, dir(-40)); | ||
| + | dot("$P$", P, dir(50)); | ||
| + | dot("$Q$", Q, dir(-170)); | ||
| + | dot("$M$", M, dir(-50)); | ||
| + | dot("$N$", N, dir(-140)); | ||
| + | dot("$T$", T,dir(-90)); | ||
| + | dot("$L$", L, dir(-120)); | ||
| + | </asy> | ||
--[[User:Suli|Suli]] 10:38, 8 February 2015 (EST) | --[[User:Suli|Suli]] 10:38, 8 February 2015 (EST) | ||
| + | |||
| + | ===Solution 4=== | ||
| + | Let <math>D_1</math> be the second intersection of <math>NC</math> with the circumcircle of <math>\triangle ABC,</math> and <math>D_2</math> the second intersection of <math>MB</math> with the circumcircle of <math>\triangle ABC.</math> By inscribed angles, the tangent at <math>C</math> is parallel to <math>AN.</math> Let <math>P_{\infty}</math> denote the point at infinity along line <math>AN.</math> Note that <cmath>(A,D_1;B,C)\stackrel{C}{=}(A,N;Q,P_{\infty})=-1.</cmath> So, <math>ABD_1C</math> is harmonic. Similarly, we can find <math>ABD_2C</math> is harmonic. Therefore, <math>D_1=D_2,</math> which means that <math>BM</math> and <math>CN</math> intersect on the circumcircle. <math>\blacksquare</math> | ||
| + | |||
| + | === Solution 5 === | ||
| + | |||
| + | We use barycentric coordinates. Due to the equal angles, <math>AC</math> is tangent to the circumcircle of <math>ABQ</math> and <math>AB</math> is tangent to the circumcircle of the <math>APC.</math> Therefore, we can use power of a point to solve for side ratios. We have <cmath>A=(1,0,0), B=(0,1,0), C=(0,0,1)</cmath> <cmath>P=(0:a^2-c^2:c^2),Q=(0:b^2:a^2-b^2)</cmath> <cmath>M=(-a^2:2a^2-2c^2:2c^2),N=(-a^2:2b^2:2a^2-2b^2)</cmath> | ||
| + | Therefore, <math>D=(-a^2:2b^2:2c^2),</math> as <math>BM</math> and <math>CN</math> are cevians. Note that <math>(x,y,z)</math> lies on the circumcircle iff <math>a^2yz+b^2xz+c^2xy=0.</math> Substituting the values in, we have <cmath>-4a^2b^2c^2+2a^2b^2c^2+2a^2b^2c^2=0,</cmath> so we are done. <math>\blacksquare</math> | ||
| + | |||
| + | === Solution 6 === | ||
| + | Note that the givens immediately imply that <math>\triangle{ABC} \sim \triangle{QAC} \sim \triangle{PBA}</math>, hence <math>\angle{AQP}=\angle{APQ}=\angle{A}</math>. Let <math>D</math> be the midpoint of BC, <math>E</math> be the midpoint of <math>AC</math>, and <math>F</math> the midpoint of <math>AB</math>. By the similar triangles, we have <math>\angle{BAD}=\angle{AQE}=\angle{AMC}</math>. We also have <math>\angle{BAD}=\angle{BPF}=\angle{MNB}</math>, so we find <math>\angle{AMC}=\angle{MNB}</math>. We note that <math>\angle{AMC}+\angle{CMN}=\angle{AMN}=\angle{AQP}=\angle{A}</math>, so <math>\angle{CMN}+\angle{MNB}=A</math>, which gives that <math>\angle{BKC}=180-\angle{A}</math> and we are done. | ||
| + | |||
| + | As an addition, <math>AK</math> is the A-symmedian in <math>\triangle{ABC}</math>. | ||
| + | |||
| + | === Solution 7 (Pascal Theorem) === | ||
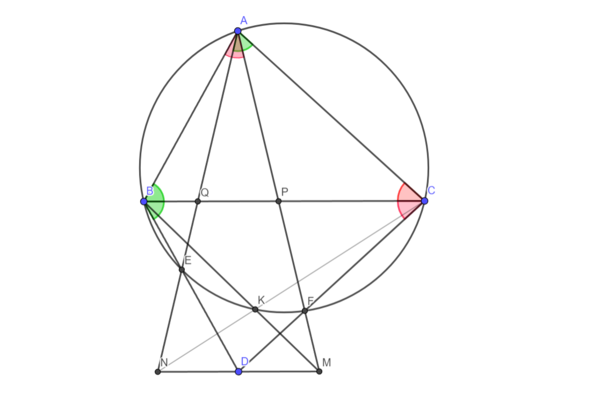
| + | [[File:IMO2014 P4.png|600px|up]] | ||
| + | |||
| + | Let <math>w</math> be the circumcircle of <math>\triangle{ABC}</math>. Let <math>E</math> and <math>F</math> be the intersection of <math>w</math> with <math>AQ</math> and <math>AP</math>, respectively. By basic angle chasing, we have <math>\angle{ABC} = \angle{CBE}</math> and <math>\angle{ACB} = \angle{BCF}</math>. So if the intersection of <math>BE</math> and <math>CF</math> is <math>D</math>, <math>BC</math> bisects <math>AD</math>. And we know that <math>BC</math> bisects <math>AN</math> and <math>AM</math>, that means <math>N</math>, <math>D</math> and <math>M</math> are collinear. Now, we define the point <math>K</math> which is the intersection of <math>BM</math> and <math>w</math>. And let us say <math>X</math> to the intersection of <math>CK</math> and <math>AE</math>. By Pascal Theorem at <math>FCKBEA</math>: | ||
| + | |||
| + | <math>D</math>, <math>X</math> and <math>M</math> are collinear. That means <math>X</math> is on <math>DM</math>, <math>CK</math> and <math>AE</math>. Therefore <math>X = N</math> and this ends the proof because the intersection of <math>CN</math> and <math>BM</math> is the point <math>K</math> which is on <math>w</math>. <math>\blacksquare</math> | ||
| + | |||
| + | ~Ege Saribas | ||
{{alternate solutions}} | {{alternate solutions}} | ||
Latest revision as of 13:36, 1 June 2024
Contents
Problem
Points ![]() and
and ![]() lie on side
lie on side ![]() of acute-angled
of acute-angled ![]() so that
so that ![]() and
and ![]() . Points
. Points ![]() and
and ![]() lie on lines
lie on lines ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() . Prove that lines
. Prove that lines ![]() and
and ![]() intersect on the circumcircle of
intersect on the circumcircle of ![]() .
.
Solution
Solution 1
![[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki, go to User:Azjps/geogebra */ import graph; size(10.60000000000002cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -4.740000000000007, xmax = 16.46000000000002, ymin = -7.520000000000004, ymax = 4.140000000000004; /* image dimensions */ pen zzttqq = rgb(0.6000000000000006,0.2000000000000002,0.000000000000000); pen qqwuqq = rgb(0.000000000000000,0.3921568627450985,0.000000000000000); draw((1.800000000000002,3.640000000000004)--(-0.2200000000000002,-1.200000000000001)--(7.660000000000009,-1.140000000000001)--cycle, zzttqq); draw(arc((7.660000000000009,-1.140000000000001),0.6000000000000009,140.7958863822920,180.4362538499006)--(7.660000000000009,-1.140000000000001)--cycle, red); draw(arc((-0.2200000000000002,-1.200000000000001),0.6000000000000009,0.4362538499004549,67.34652063545073)--(-0.2200000000000002,-1.200000000000001)--cycle, qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-106.1141136177082,-39.20411361770813)--(1.800000000000002,3.640000000000004)--cycle, qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-112.6534793645495,-73.01347936454944)--(1.800000000000002,3.640000000000004)--cycle, red); /* draw figures */ draw((1.800000000000002,3.640000000000004)--(-0.2200000000000002,-1.200000000000001), zzttqq); draw((-0.2200000000000002,-1.200000000000001)--(7.660000000000009,-1.140000000000001), zzttqq); draw((7.660000000000009,-1.140000000000001)--(1.800000000000002,3.640000000000004), zzttqq); draw(arc((7.660000000000009,-1.140000000000001),0.6000000000000009,140.7958863822920,180.4362538499006), red); draw(arc((7.660000000000009,-1.140000000000001),0.5000000000000008,140.7958863822920,180.4362538499006), red); draw(arc((-0.2200000000000002,-1.200000000000001),0.6000000000000009,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((-0.2200000000000002,-1.200000000000001),0.5000000000000008,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((-0.2200000000000002,-1.200000000000001),0.4000000000000006,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.5000000000000008,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.4000000000000006,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-112.6534793645495,-73.01347936454944), red); draw(arc((1.800000000000002,3.640000000000004),0.5000000000000008,-112.6534793645495,-73.01347936454944), red); draw((-1.022670636276736,-6.130338243877306)--(7.660000000000009,-1.140000000000001)); draw((4.740746205921980,-5.986847110107199)--(-0.2200000000000002,-1.200000000000001)); draw((1.800000000000002,3.640000000000004)--(4.740746205921980,-5.986847110107199)); draw((1.800000000000002,3.640000000000004)--(-1.022670636276736,-6.130338243877306)); draw(circle((3.711084749329270,0.0008695880898521494), 4.110415438128883)); /* dots and labels */ dot((1.800000000000002,3.640000000000004),dotstyle); label("$A$", (1.880000000000002,3.760000000000004), NE * labelscalefactor); dot((-0.2200000000000002,-1.200000000000001),dotstyle); label("$B$", (-0.1400000000000008,-1.080000000000000), NE * labelscalefactor); dot((7.660000000000009,-1.140000000000001),dotstyle); label("$C$", (7.740000000000012,-1.020000000000000), NE * labelscalefactor); dot((0.3886646818616330,-1.245169121938651),dotstyle); label("$Q$", (0.4600000000000001,-1.120000000000000), NE * labelscalefactor); dot((3.270373102960991,-1.173423555053598),dotstyle); label("$P$", (3.360000000000004,-1.060000000000000), NE * labelscalefactor); dot((4.740746205921980,-5.986847110107199),dotstyle); label("$M$", (4.820000000000006,-5.860000000000003), NE * labelscalefactor); dot((-1.022670636276736,-6.130338243877306),dotstyle); label("$N$", (-0.9400000000000020,-6.020000000000004), NE * labelscalefactor); dot((2.709057008802497,-3.985539257126989),dotstyle); label("$D$", (2.780000000000003,-3.860000000000002), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]](http://latex.artofproblemsolving.com/0/8/8/088e13223b4887f9d60d871fc8c76363a0bed975.png)
We are trying to prove that the intersection of ![]() and
and ![]() , call it point
, call it point ![]() , is on the circumcircle of triangle
, is on the circumcircle of triangle ![]() . In other words, we are trying to prove
. In other words, we are trying to prove ![]() .
Let the intersection of
.
Let the intersection of ![]() and
and ![]() be point
be point ![]() , and the intersection of
, and the intersection of ![]() and
and ![]() be point
be point ![]() .
Let us assume
.
Let us assume ![]() . Note: This is circular reasoning. If
. Note: This is circular reasoning. If ![]() , then
, then ![]() should be equal to
should be equal to ![]() and
and ![]() . We can quickly prove that the triangles
. We can quickly prove that the triangles ![]() ,
, ![]() , and
, and ![]() are similar, so
are similar, so ![]() . We also see that
. We also see that ![]() . Also because angles
. Also because angles ![]() and
and ![]() and
and ![]() are equal, the triangles
are equal, the triangles ![]() and
and ![]() ,
, ![]() and
and ![]() must be two pairs of similar triangles. Therefore we must prove angles
must be two pairs of similar triangles. Therefore we must prove angles ![]() and
and ![]() and
and ![]() are equal.
We have angles
are equal.
We have angles ![]() . We also have
. We also have ![]() ,
, ![]() . Because the triangles
. Because the triangles ![]() and
and ![]() are similar, we have
are similar, we have ![]() , so triangles
, so triangles ![]() and
and ![]() are similar. So the angles
are similar. So the angles ![]() and
and ![]() and
and ![]() are equal and we are done.
are equal and we are done.
Solution 2
Let ![]() be the midpoint of
be the midpoint of ![]() . Easy angle chasing gives
. Easy angle chasing gives ![]() . Because
. Because ![]() is the midpoint of
is the midpoint of ![]() , the cotangent rule applied on triangle
, the cotangent rule applied on triangle ![]() gives us
gives us
![]() Hence, by the cotangent rule on
Hence, by the cotangent rule on ![]() , we have
, we have
![]() Because the period of cotangent is
Because the period of cotangent is ![]() , but angles are less than
, but angles are less than ![]() , we have
, we have ![]()
Similarly, we have ![]() Hence, if
Hence, if ![]() and
and ![]() intersect at
intersect at ![]() , then
, then ![]() by the Angle Sum in a Triangle Theorem. Hence,
by the Angle Sum in a Triangle Theorem. Hence, ![]() is cyclic, which is equivalent to the desired result.
is cyclic, which is equivalent to the desired result.
--Suli 23:27, 7 February 2015 (EST)
Solution 3
Let ![]() be the midpoint of
be the midpoint of ![]() . By AA Similarity, triangles
. By AA Similarity, triangles ![]() and
and ![]() are similar, so
are similar, so ![]() and
and ![]() . Similarly,
. Similarly, ![]() , and so triangle
, and so triangle ![]() is isosceles. Thus,
is isosceles. Thus, ![]() , and so
, and so ![]() . Dividing both sides by 2, we have
. Dividing both sides by 2, we have ![]() , or
, or
![]() But we also have
But we also have ![]() , so triangles
, so triangles ![]() and
and ![]() are similar by
are similar by ![]() similarity. In particular,
similarity. In particular, ![]() . Similarly,
. Similarly, ![]() , so
, so ![]() . In addition, angle sum in triangle
. In addition, angle sum in triangle ![]() gives
gives ![]() . Therefore, if we let lines
. Therefore, if we let lines ![]() and
and ![]() intersect at
intersect at ![]() , by Angle Sum in quadrilateral
, by Angle Sum in quadrilateral ![]() concave
concave ![]() , and so convex
, and so convex ![]() , which is enough to prove that
, which is enough to prove that ![]() is cyclic. This completes the proof.
is cyclic. This completes the proof.
![[asy] size(250); defaultpen(fontsize(8pt)); pair A = dir(110); pair B = dir(210); pair C = dir(330); pair Pp = rotate(50, A)*B; pair P = extension(A,Pp,B,C); pair Qp = rotate(-70, A)*C; pair Q = extension(A,Qp,B,C); pair M = rotate(180,P)*A; pair N = rotate(180,Q)*A; path c1 = circumcircle(A,B,C); pair T = IP(B--M,C--N); pair L = midpoint(B--C); draw(A--B--C--cycle^^B--Q--A--P^^Q--N--C^^P--M--B^^A--L); draw(c1); dot("$A$", A, dir(100)); dot("$B$", B, dir(-110)); dot("$C$", C, dir(-40)); dot("$P$", P, dir(50)); dot("$Q$", Q, dir(-170)); dot("$M$", M, dir(-50)); dot("$N$", N, dir(-140)); dot("$T$", T,dir(-90)); dot("$L$", L, dir(-120)); [/asy]](http://latex.artofproblemsolving.com/1/2/b/12bb205080ded2d4418e6d2e50a17bdb81f05d9f.png)
--Suli 10:38, 8 February 2015 (EST)
Solution 4
Let ![]() be the second intersection of
be the second intersection of ![]() with the circumcircle of
with the circumcircle of ![]() and
and ![]() the second intersection of
the second intersection of ![]() with the circumcircle of
with the circumcircle of ![]() By inscribed angles, the tangent at
By inscribed angles, the tangent at ![]() is parallel to
is parallel to ![]() Let
Let ![]() denote the point at infinity along line
denote the point at infinity along line ![]() Note that
Note that ![]() So,
So, ![]() is harmonic. Similarly, we can find
is harmonic. Similarly, we can find ![]() is harmonic. Therefore,
is harmonic. Therefore, ![]() which means that
which means that ![]() and
and ![]() intersect on the circumcircle.
intersect on the circumcircle. ![]()
Solution 5
We use barycentric coordinates. Due to the equal angles, ![]() is tangent to the circumcircle of
is tangent to the circumcircle of ![]() and
and ![]() is tangent to the circumcircle of the
is tangent to the circumcircle of the ![]() Therefore, we can use power of a point to solve for side ratios. We have
Therefore, we can use power of a point to solve for side ratios. We have ![]()
![]()
![]() Therefore,
Therefore, ![]() as
as ![]() and
and ![]() are cevians. Note that
are cevians. Note that ![]() lies on the circumcircle iff
lies on the circumcircle iff ![]() Substituting the values in, we have
Substituting the values in, we have ![]() so we are done.
so we are done. ![]()
Solution 6
Note that the givens immediately imply that ![]() , hence
, hence ![]() . Let
. Let ![]() be the midpoint of BC,
be the midpoint of BC, ![]() be the midpoint of
be the midpoint of ![]() , and
, and ![]() the midpoint of
the midpoint of ![]() . By the similar triangles, we have
. By the similar triangles, we have ![]() . We also have
. We also have ![]() , so we find
, so we find ![]() . We note that
. We note that ![]() , so
, so ![]() , which gives that
, which gives that ![]() and we are done.
and we are done.
As an addition, ![]() is the A-symmedian in
is the A-symmedian in ![]() .
.
Solution 7 (Pascal Theorem)
Let ![]() be the circumcircle of
be the circumcircle of ![]() . Let
. Let ![]() and
and ![]() be the intersection of
be the intersection of ![]() with
with ![]() and
and ![]() , respectively. By basic angle chasing, we have
, respectively. By basic angle chasing, we have ![]() and
and ![]() . So if the intersection of
. So if the intersection of ![]() and
and ![]() is
is ![]() ,
, ![]() bisects
bisects ![]() . And we know that
. And we know that ![]() bisects
bisects ![]() and
and ![]() , that means
, that means ![]() ,
, ![]() and
and ![]() are collinear. Now, we define the point
are collinear. Now, we define the point ![]() which is the intersection of
which is the intersection of ![]() and
and ![]() . And let us say
. And let us say ![]() to the intersection of
to the intersection of ![]() and
and ![]() . By Pascal Theorem at
. By Pascal Theorem at ![]() :
:
![]() ,
, ![]() and
and ![]() are collinear. That means
are collinear. That means ![]() is on
is on ![]() ,
, ![]() and
and ![]() . Therefore
. Therefore ![]() and this ends the proof because the intersection of
and this ends the proof because the intersection of ![]() and
and ![]() is the point
is the point ![]() which is on
which is on ![]() .
. ![]()
~Ege Saribas
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See Also
| 2014 IMO (Problems) • Resources | ||
| Preceded by Problem 3 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 5 |
| All IMO Problems and Solutions | ||