Difference between revisions of "2014 IMO Problems/Problem 4"

Latest revision as of 13:36, 1 June 2024

Problem

Points $P$ and $Q$ lie on side $BC$ of acute-angled $\triangle{ABC}$ so that $\angle{PAB}=\angle{BCA}$ and $\angle{CAQ}=\angle{ABC}$ . Points $M$ and $N$ lie on lines $AP$ and $AQ$ , respectively, such that $P$ is the midpoint of $AM$ , and $Q$ is the midpoint of $AN$ . Prove that lines $BM$ and $CN$ intersect on the circumcircle of $\triangle{ABC}$ .

Solution

Solution 1

$[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki, go to User:Azjps/geogebra */ import graph; size(10.60000000000002cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -4.740000000000007, xmax = 16.46000000000002, ymin = -7.520000000000004, ymax = 4.140000000000004; /* image dimensions */ pen zzttqq = rgb(0.6000000000000006,0.2000000000000002,0.000000000000000); pen qqwuqq = rgb(0.000000000000000,0.3921568627450985,0.000000000000000); draw((1.800000000000002,3.640000000000004)--(-0.2200000000000002,-1.200000000000001)--(7.660000000000009,-1.140000000000001)--cycle, zzttqq); draw(arc((7.660000000000009,-1.140000000000001),0.6000000000000009,140.7958863822920,180.4362538499006)--(7.660000000000009,-1.140000000000001)--cycle, red); draw(arc((-0.2200000000000002,-1.200000000000001),0.6000000000000009,0.4362538499004549,67.34652063545073)--(-0.2200000000000002,-1.200000000000001)--cycle, qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-106.1141136177082,-39.20411361770813)--(1.800000000000002,3.640000000000004)--cycle, qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-112.6534793645495,-73.01347936454944)--(1.800000000000002,3.640000000000004)--cycle, red); /* draw figures */ draw((1.800000000000002,3.640000000000004)--(-0.2200000000000002,-1.200000000000001), zzttqq); draw((-0.2200000000000002,-1.200000000000001)--(7.660000000000009,-1.140000000000001), zzttqq); draw((7.660000000000009,-1.140000000000001)--(1.800000000000002,3.640000000000004), zzttqq); draw(arc((7.660000000000009,-1.140000000000001),0.6000000000000009,140.7958863822920,180.4362538499006), red); draw(arc((7.660000000000009,-1.140000000000001),0.5000000000000008,140.7958863822920,180.4362538499006), red); draw(arc((-0.2200000000000002,-1.200000000000001),0.6000000000000009,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((-0.2200000000000002,-1.200000000000001),0.5000000000000008,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((-0.2200000000000002,-1.200000000000001),0.4000000000000006,0.4362538499004549,67.34652063545073), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.5000000000000008,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.4000000000000006,-106.1141136177082,-39.20411361770813), qqwuqq); draw(arc((1.800000000000002,3.640000000000004),0.6000000000000009,-112.6534793645495,-73.01347936454944), red); draw(arc((1.800000000000002,3.640000000000004),0.5000000000000008,-112.6534793645495,-73.01347936454944), red); draw((-1.022670636276736,-6.130338243877306)--(7.660000000000009,-1.140000000000001)); draw((4.740746205921980,-5.986847110107199)--(-0.2200000000000002,-1.200000000000001)); draw((1.800000000000002,3.640000000000004)--(4.740746205921980,-5.986847110107199)); draw((1.800000000000002,3.640000000000004)--(-1.022670636276736,-6.130338243877306)); draw(circle((3.711084749329270,0.0008695880898521494), 4.110415438128883)); /* dots and labels */ dot((1.800000000000002,3.640000000000004),dotstyle); label("$A$", (1.880000000000002,3.760000000000004), NE * labelscalefactor); dot((-0.2200000000000002,-1.200000000000001),dotstyle); label("$B$", (-0.1400000000000008,-1.080000000000000), NE * labelscalefactor); dot((7.660000000000009,-1.140000000000001),dotstyle); label("$C$", (7.740000000000012,-1.020000000000000), NE * labelscalefactor); dot((0.3886646818616330,-1.245169121938651),dotstyle); label("$Q$", (0.4600000000000001,-1.120000000000000), NE * labelscalefactor); dot((3.270373102960991,-1.173423555053598),dotstyle); label("$P$", (3.360000000000004,-1.060000000000000), NE * labelscalefactor); dot((4.740746205921980,-5.986847110107199),dotstyle); label("$M$", (4.820000000000006,-5.860000000000003), NE * labelscalefactor); dot((-1.022670636276736,-6.130338243877306),dotstyle); label("$N$", (-0.9400000000000020,-6.020000000000004), NE * labelscalefactor); dot((2.709057008802497,-3.985539257126989),dotstyle); label("$D$", (2.780000000000003,-3.860000000000002), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]$

We are trying to prove that the intersection of $BM$ and $CN$ , call it point $D$ , is on the circumcircle of triangle $ABC$ . In other words, we are trying to prove $\angle {BDC} + \angle {BAC} = 180$ . Let the intersection of $BM$ and $AN$ be point $E$ , and the intersection of $AM$ and $CN$ be point $F$ . Let us assume $\angle {BDC} + \angle {BAC} = 180$ . Note: This is circular reasoning. If $\angle {BDC} + \angle {BAC} = 180$ , then $\angle {BAC}$ should be equal to $\angle {BDN}$ and $\angle {CDM}$ . We can quickly prove that the triangles $ABC$ , $APB$ , and $AQC$ are similar, so $\angle {BAC} = \angle {AQC} = \angle {APB}$ . We also see that $\angle {AQC} = \angle {BQN} = \angle {APB} = \angle {CPF}$ . Also because angles $BEQ$ and $NED, MFD$ and $CFP$ are equal, the triangles $BEQ$ and $NED$ , $MDF$ and $FCP$ must be two pairs of similar triangles. Therefore we must prove angles $CBM$ and $ANC, AMB$ and $BCN$ are equal. We have angles $BQA = APC = NQC = BPM$ . We also have $AQ = QN$ , $AP = PM$ . Because the triangles $ABP$ and $ACQ$ are similar, we have $\dfrac {EC}{EN} = \dfrac {BF}{FM}$ , so triangles $BFM$ and $NEC$ are similar. So the angles $CBM$ and $ANC, BCN$ and $AMB$ are equal and we are done.

Solution 2

Let $L$ be the midpoint of $BC$ . Easy angle chasing gives $\angle{AQP} = \angle{APQ} = \angle{BAC}$ . Because $P$ is the midpoint of $AM$ , the cotangent rule applied on triangle $MBA$ gives us $\cot \angle{MBC} - \cot \angle{ABC} = 2\cot \angle{BAC}.$ Hence, by the cotangent rule on $ABC$ , we have $\cot \angle{BAL} = 2\cot \angle{BAC} + \cot \angle{ABC} = \cot \angle{MBC}.$ Because the period of cotangent is $180^\circ$ , but angles are less than $180^\circ$ , we have $\angle{BAL} = \angle{MBC}.$

Similarly, we have $\angle{LAC} = \angle{NCB}.$ Hence, if $BM$ and $CN$ intersect at $Z$ , then $\angle{BZC} = 180^\circ - \angle{BAC}$ by the Angle Sum in a Triangle Theorem. Hence, $BACZ$ is cyclic, which is equivalent to the desired result.

--Suli 23:27, 7 February 2015 (EST)

Solution 3

Let $L$ be the midpoint of $BC$ . By AA Similarity, triangles $BAP$ and $BCA$ are similar, so $\dfrac{BA}{AP} = \dfrac{BC}{CA}$ and $\angle{BPA} = \angle{BAC}$ . Similarly, $\angle{CQA} = \angle{BAC}$ , and so triangle $AQP$ is isosceles. Thus, $AQ = AP$ , and so $\dfrac{BA}{AQ} = \dfrac{BC}{CA}$ . Dividing both sides by 2, we have $\dfrac{BA}{AN} = \dfrac{BL}{AC}$ , or $\frac{BA}{BL} = \frac{AN}{AC}.$ But we also have $\angle{ABL} = \angle{CAQ}$ , so triangles $ABL$ and $NAC$ are similar by $SAS$ similarity. In particular, $\angle{ANC} = \angle{BAL}$ . Similarly, $\angle{BMA} = \angle{CAL}$ , so $\angle{ANC} + \angle{BMA} = \angle{BAC}$ . In addition, angle sum in triangle $AQP$ gives $\angle{QAP} = 180^\circ - 2\angle{A}$ . Therefore, if we let lines $BM$ and $CN$ intersect at $T$ , by Angle Sum in quadrilateral $AMTN$ concave $\angle{NTM} = 180^\circ + \angle{A}$ , and so convex $\angle{BTC} = 180^\circ - \angle{A}$ , which is enough to prove that $BACT$ is cyclic. This completes the proof.

$[asy] size(250); defaultpen(fontsize(8pt)); pair A = dir(110); pair B = dir(210); pair C = dir(330); pair Pp = rotate(50, A)*B; pair P = extension(A,Pp,B,C); pair Qp = rotate(-70, A)*C; pair Q = extension(A,Qp,B,C); pair M = rotate(180,P)*A; pair N = rotate(180,Q)*A; path c1 = circumcircle(A,B,C); pair T = IP(B--M,C--N); pair L = midpoint(B--C); draw(A--B--C--cycle^^B--Q--A--P^^Q--N--C^^P--M--B^^A--L); draw(c1); dot("$A$", A, dir(100)); dot("$B$", B, dir(-110)); dot("$C$", C, dir(-40)); dot("$P$", P, dir(50)); dot("$Q$", Q, dir(-170)); dot("$M$", M, dir(-50)); dot("$N$", N, dir(-140)); dot("$T$", T,dir(-90)); dot("$L$", L, dir(-120)); [/asy]$

--Suli 10:38, 8 February 2015 (EST)

Solution 4

Let $D_1$ be the second intersection of $NC$ with the circumcircle of $\triangle ABC,$ and $D_2$ the second intersection of $MB$ with the circumcircle of $\triangle ABC.$ By inscribed angles, the tangent at $C$ is parallel to $AN.$ Let $P_{\infty}$ denote the point at infinity along line $AN.$ Note that $(A,D_1;B,C)\stackrel{C}{=}(A,N;Q,P_{\infty})=-1.$ So, $ABD_1C$ is harmonic. Similarly, we can find $ABD_2C$ is harmonic. Therefore, $D_1=D_2,$ which means that $BM$ and $CN$ intersect on the circumcircle. $\blacksquare$

Solution 5

We use barycentric coordinates. Due to the equal angles, $AC$ is tangent to the circumcircle of $ABQ$ and $AB$ is tangent to the circumcircle of the $APC.$ Therefore, we can use power of a point to solve for side ratios. We have $A=(1,0,0), B=(0,1,0), C=(0,0,1)$ $P=(0:a^2-c^2:c^2),Q=(0:b^2:a^2-b^2)$ $M=(-a^2:2a^2-2c^2:2c^2),N=(-a^2:2b^2:2a^2-2b^2)$ Therefore, $D=(-a^2:2b^2:2c^2),$ as $BM$ and $CN$ are cevians. Note that $(x,y,z)$ lies on the circumcircle iff $a^2yz+b^2xz+c^2xy=0.$ Substituting the values in, we have $-4a^2b^2c^2+2a^2b^2c^2+2a^2b^2c^2=0,$ so we are done. $\blacksquare$

Solution 6

Note that the givens immediately imply that $\triangle{ABC} \sim \triangle{QAC} \sim \triangle{PBA}$ , hence $\angle{AQP}=\angle{APQ}=\angle{A}$ . Let $D$ be the midpoint of BC, $E$ be the midpoint of $AC$ , and $F$ the midpoint of $AB$ . By the similar triangles, we have $\angle{BAD}=\angle{AQE}=\angle{AMC}$ . We also have $\angle{BAD}=\angle{BPF}=\angle{MNB}$ , so we find $\angle{AMC}=\angle{MNB}$ . We note that $\angle{AMC}+\angle{CMN}=\angle{AMN}=\angle{AQP}=\angle{A}$ , so $\angle{CMN}+\angle{MNB}=A$ , which gives that $\angle{BKC}=180-\angle{A}$ and we are done.

As an addition, $AK$ is the A-symmedian in $\triangle{ABC}$ .

Solution 7 (Pascal Theorem)

Let $w$ be the circumcircle of $\triangle{ABC}$ . Let $E$ and $F$ be the intersection of $w$ with $AQ$ and $AP$ , respectively. By basic angle chasing, we have $\angle{ABC} = \angle{CBE}$ and $\angle{ACB} = \angle{BCF}$ . So if the intersection of $BE$ and $CF$ is $D$ , $BC$ bisects $AD$ . And we know that $BC$ bisects $AN$ and $AM$ , that means $N$ , $D$ and $M$ are collinear. Now, we define the point $K$ which is the intersection of $BM$ and $w$ . And let us say $X$ to the intersection of $CK$ and $AE$ . By Pascal Theorem at $FCKBEA$ :

$D$ , $X$ and $M$ are collinear. That means $X$ is on $DM$ , $CK$ and $AE$ . Therefore $X = N$ and this ends the proof because the intersection of $CN$ and $BM$ is the point $K$ which is on $w$ . $\blacksquare$

~Ege Saribas

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

@@ Line 3: / Line 3: @@
 ==Solution==
+===Solution 1===
 <asy>
   /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki, go to User:Azjps/geogebra */
@@ Line 57: / Line 58: @@
 </asy>
-We are trying to prove that the intersection of <math>BM</math> and <math>CN</math>, call it point <math>D</math>, is on the circumcircle of triangle <math>ABC</math>. In other words, we are trying to prove angle <math>BAC</math> plus angle <math>BDC</math> is 180 degrees.
+We are trying to prove that the intersection of <math>BM</math> and <math>CN</math>, call it point <math>D</math>, is on the circumcircle of triangle <math>ABC</math>. In other words, we are trying to prove <math>\angle {BDC} + \angle {BAC} = 180</math>.
 Let the intersection of <math>BM</math> and <math>AN</math> be point <math>E</math>, and the intersection of <math>AM</math> and <math>CN</math> be point <math>F</math>.
-Let us assume (angle <math>BDC</math>) + (angle <math>BAC</math>) = 180. ''Note: This is circular reasoning.'' If angle <math>BDC</math> plus angle <math>BAC</math> is 180, then angle <math>BAC</math> should be equal to angles <math>BDN</math> and <math>CDM</math>. We can quickly prove that the triangles <math>ABC</math>, <math>APB</math>, and <math>AQC</math> are similar, so angles <math>BAC</math> = <math>AQC</math> = <math>APB</math>. We also see that angles <math>AQC = BQN = APB = CPF</math>. Also because angles <math>BEQ</math> and <math>NED, MFD</math> and <math>CFP</math> are equal, the triangles <math>BEQ</math> and <math>NED</math>, <math>MDF</math> and <math>FCP</math> must be two pairs of similar triangles. Therefore we must prove angles <math>CBM</math> and <math>ANC, AMB</math> and <math>BCN</math> are equal.
+Let us assume <math>\angle {BDC} + \angle {BAC} = 180</math>. ''Note: This is circular reasoning.'' If <math>\angle {BDC} + \angle {BAC} = 180</math>, then <math>\angle {BAC}</math> should be equal to <math>\angle {BDN}</math> and <math>\angle {CDM}</math>. We can quickly prove that the triangles <math>ABC</math>, <math>APB</math>, and <math>AQC</math> are similar, so <math>\angle {BAC} = \angle {AQC} = \angle {APB}</math>. We also see that <math>\angle {AQC} = \angle {BQN} = \angle {APB} = \angle {CPF}</math>. Also because angles <math>BEQ</math> and <math>NED, MFD</math> and <math>CFP</math> are equal, the triangles <math>BEQ</math> and <math>NED</math>, <math>MDF</math> and <math>FCP</math> must be two pairs of similar triangles. Therefore we must prove angles <math>CBM</math> and <math>ANC, AMB</math> and <math>BCN</math> are equal.
-We have angles <math>BQA = APC = NQC = BPM</math>. We also have <math>AQ = QN</math>, <math>AP = PM</math>. Because the triangles <math>ABP</math> and <math>ACQ</math> are similar, we have <math>EC/EN = BF/FM</math>, so triangles <math>BFM</math> and <math>NEC</math> are similar. So the angles <math>CBM</math> and <math>ANC, BCN</math> and <math>AMB</math> are equal and we are done.
+We have angles <math>BQA = APC = NQC = BPM</math>. We also have <math>AQ = QN</math>, <math>AP = PM</math>. Because the triangles <math>ABP</math> and <math>ACQ</math> are similar, we have <math>\dfrac {EC}{EN} = \dfrac {BF}{FM}</math>, so triangles <math>BFM</math> and <math>NEC</math> are similar. So the angles <math>CBM</math> and <math>ANC, BCN</math> and <math>AMB</math> are equal and we are done.
-==Solution 2==
+===Solution 2===
 Let <math>L</math> be the midpoint of <math>BC</math>. Easy angle chasing gives <math>\angle{AQP} = \angle{APQ} = \angle{BAC}</math>. Because <math>P</math> is the midpoint of <math>AM</math>, the cotangent rule applied on triangle <math>MBA</math> gives us
 <cmath>\cot \angle{MBC} - \cot \angle{ABC} = 2\cot \angle{BAC}.</cmath>
@@ Line 73: / Line 74: @@
 --[[User:Suli|Suli]] 23:27, 7 February 2015 (EST)
-==Solution 3==
+===Solution 3===
 Let <math>L</math> be the midpoint of <math>BC</math>. By AA Similarity, triangles <math>BAP</math> and <math>BCA</math> are similar, so <math>\dfrac{BA}{AP} = \dfrac{BC}{CA}</math> and <math>\angle{BPA} = \angle{BAC}</math>. Similarly, <math>\angle{CQA} = \angle{BAC}</math>, and so triangle <math>AQP</math> is isosceles. Thus, <math>AQ = AP</math>, and so <math>\dfrac{BA}{AQ} = \dfrac{BC}{CA}</math>. Dividing both sides by 2, we have <math>\dfrac{BA}{AN} = \dfrac{BL}{AC}</math>, or
 <cmath>\frac{BA}{BL} = \frac{AN}{AC}.</cmath>
 But we also have <math>\angle{ABL} = \angle{CAQ}</math>, so triangles <math>ABL</math> and <math>NAC</math> are similar by <math>SAS</math> similarity. In particular, <math>\angle{ANC} = \angle{BAL}</math>. Similarly, <math>\angle{BMA} = \angle{CAL}</math>, so <math>\angle{ANC} + \angle{BMA} = \angle{BAC}</math>. In addition, angle sum in triangle <math>AQP</math> gives <math>\angle{QAP} = 180^\circ - 2\angle{A}</math>. Therefore, if we let lines <math>BM</math> and <math>CN</math> intersect at <math>T</math>, by Angle Sum in quadrilateral <math>AMTN</math> concave <math>\angle{NTM} = 180^\circ + \angle{A}</math>, and so convex <math>\angle{BTC} = 180^\circ - \angle{A}</math>, which is enough to prove that <math>BACT</math> is cyclic. This completes the proof.
+<asy>
+size(250);
+defaultpen(fontsize(8pt));
+pair A = dir(110);
+pair B = dir(210);
+pair C = dir(330);
+pair Pp = rotate(50, A)*B;
+pair P = extension(A,Pp,B,C);
+pair Qp = rotate(-70, A)*C;
+pair Q = extension(A,Qp,B,C);
+pair M = rotate(180,P)*A;
+pair N = rotate(180,Q)*A;
+path c1 = circumcircle(A,B,C);
+pair T = IP(B--M,C--N);
+pair L = midpoint(B--C);
+draw(A--B--C--cycle^^B--Q--A--P^^Q--N--C^^P--M--B^^A--L);
+draw(c1);
+dot("$A$", A, dir(100));
+dot("$B$", B, dir(-110));
+dot("$C$", C, dir(-40));
+dot("$P$", P, dir(50));
+dot("$Q$", Q, dir(-170));
+dot("$M$", M, dir(-50));
+dot("$N$", N, dir(-140));
+dot("$T$", T,dir(-90));
+dot("$L$", L, dir(-120));
+</asy>
 --[[User:Suli|Suli]] 10:38, 8 February 2015 (EST)
+===Solution 4===
+Let <math>D_1</math> be the second intersection of <math>NC</math> with the circumcircle of <math>\triangle ABC,</math> and <math>D_2</math> the second intersection of <math>MB</math> with the circumcircle of <math>\triangle ABC.</math> By inscribed angles, the tangent at <math>C</math> is parallel to <math>AN.</math> Let <math>P_{\infty}</math> denote the point at infinity along line <math>AN.</math> Note that <cmath>(A,D_1;B,C)\stackrel{C}{=}(A,N;Q,P_{\infty})=-1.</cmath> So, <math>ABD_1C</math> is harmonic. Similarly, we can find <math>ABD_2C</math> is harmonic. Therefore, <math>D_1=D_2,</math> which means that <math>BM</math> and <math>CN</math> intersect on the circumcircle. <math>\blacksquare</math>
+=== Solution 5 ===
+We use barycentric coordinates. Due to the equal angles, <math>AC</math> is tangent to the circumcircle of <math>ABQ</math> and <math>AB</math> is tangent to the circumcircle of the <math>APC.</math> Therefore, we can use power of a point to solve for side ratios. We have <cmath>A=(1,0,0), B=(0,1,0), C=(0,0,1)</cmath> <cmath>P=(0:a^2-c^2:c^2),Q=(0:b^2:a^2-b^2)</cmath> <cmath>M=(-a^2:2a^2-2c^2:2c^2),N=(-a^2:2b^2:2a^2-2b^2)</cmath>
+Therefore, <math>D=(-a^2:2b^2:2c^2),</math> as <math>BM</math> and <math>CN</math> are cevians. Note that <math>(x,y,z)</math> lies on the circumcircle iff <math>a^2yz+b^2xz+c^2xy=0.</math> Substituting the values in, we have <cmath>-4a^2b^2c^2+2a^2b^2c^2+2a^2b^2c^2=0,</cmath> so we are done. <math>\blacksquare</math>
+=== Solution 6 ===
+Note that the givens immediately imply that <math>\triangle{ABC} \sim \triangle{QAC} \sim \triangle{PBA}</math>, hence <math>\angle{AQP}=\angle{APQ}=\angle{A}</math>. Let <math>D</math> be the midpoint of BC, <math>E</math> be the midpoint of <math>AC</math>, and <math>F</math> the midpoint of <math>AB</math>. By the similar triangles, we have <math>\angle{BAD}=\angle{AQE}=\angle{AMC}</math>. We also have <math>\angle{BAD}=\angle{BPF}=\angle{MNB}</math>, so we find <math>\angle{AMC}=\angle{MNB}</math>. We note that <math>\angle{AMC}+\angle{CMN}=\angle{AMN}=\angle{AQP}=\angle{A}</math>, so <math>\angle{CMN}+\angle{MNB}=A</math>, which gives that <math>\angle{BKC}=180-\angle{A}</math> and we are done.
+As an addition, <math>AK</math> is the A-symmedian in <math>\triangle{ABC}</math>.
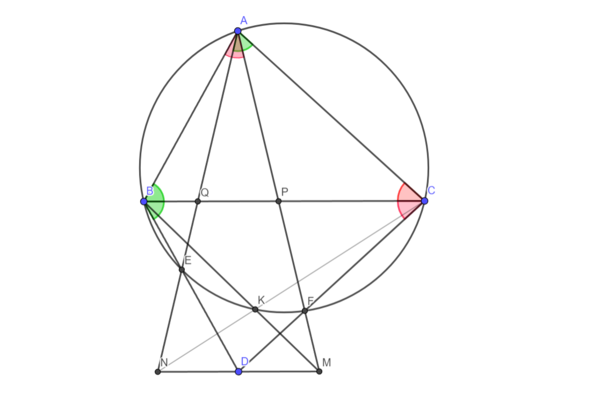
+=== Solution 7 (Pascal Theorem) ===
+[[File:IMO2014 P4.png|600px|up]]
+Let <math>w</math> be the circumcircle of <math>\triangle{ABC}</math>. Let <math>E</math> and <math>F</math> be the intersection of <math>w</math> with <math>AQ</math> and <math>AP</math>, respectively. By basic angle chasing, we have <math>\angle{ABC} = \angle{CBE}</math> and <math>\angle{ACB} = \angle{BCF}</math>. So if the intersection of <math>BE</math> and <math>CF</math> is <math>D</math>, <math>BC</math> bisects <math>AD</math>. And we know that <math>BC</math> bisects <math>AN</math> and <math>AM</math>, that means <math>N</math>, <math>D</math> and <math>M</math> are collinear. Now, we define the point <math>K</math> which is the intersection of <math>BM</math> and <math>w</math>. And let us say <math>X</math> to the intersection of <math>CK</math> and <math>AE</math>. By Pascal Theorem at <math>FCKBEA</math>:
+<math>D</math>, <math>X</math> and <math>M</math> are collinear. That means <math>X</math> is on <math>DM</math>, <math>CK</math> and <math>AE</math>. Therefore <math>X = N</math> and this ends the proof because the intersection of <math>CN</math> and <math>BM</math> is the point <math>K</math> which is on <math>w</math>. <math>\blacksquare</math>
+~Ege Saribas
 {{alternate solutions}}

2014 IMO (Problems) • Resources
Preceded by Problem 3	1 • 2 • 3 • 4 • 5 • 6	Followed by Problem 5
All IMO Problems and Solutions

Page

Toolbox

Search