Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2015 AIME I Problems/Problem 4"

(→‎Solution 3)
m (→‎Solution 3)
 
(14 intermediate revisions by 7 users not shown)
Line 2: Line 2:
 
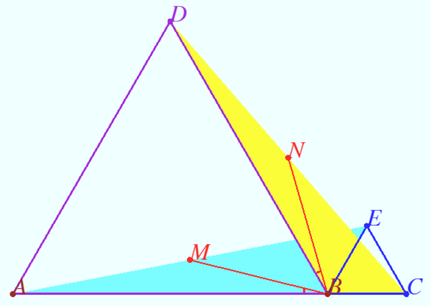
Point <math>B</math> lies on line segment <math>\overline{AC}</math> with <math>AB=16</math> and <math>BC=4</math>. Points <math>D</math> and <math>E</math> lie on the same side of line <math>AC</math> forming equilateral triangles <math>\triangle ABD</math> and <math>\triangle BCE</math>. Let <math>M</math> be the midpoint of <math>\overline{AE}</math>, and <math>N</math> be the midpoint of <math>\overline{CD}</math>. The area of <math>\triangle BMN</math> is <math>x</math>. Find <math>x^2</math>.
 
Point <math>B</math> lies on line segment <math>\overline{AC}</math> with <math>AB=16</math> and <math>BC=4</math>. Points <math>D</math> and <math>E</math> lie on the same side of line <math>AC</math> forming equilateral triangles <math>\triangle ABD</math> and <math>\triangle BCE</math>. Let <math>M</math> be the midpoint of <math>\overline{AE}</math>, and <math>N</math> be the midpoint of <math>\overline{CD}</math>. The area of <math>\triangle BMN</math> is <math>x</math>. Find <math>x^2</math>.
  
−
==Solution==
+
==Diagram==
−
Let point <math>A</math> be at <math>(0,0)</math>. Then, <math>B</math> is at <math>(16,0)</math>, and <math>C</math> is at <math>(20,0)</math>. Due to symmetry, it is allowed to assume <math>D</math> and <math>E</math> are in quadrant 1. By equilateral triangle calculations, Point <math>D</math> is at <math>(8,8\sqrt{3})</math>, and Point <math>E</math> is at <math>(18,2\sqrt{3})</math>. By Midpoint Formula, <math>M</math> is at <math>(9,\sqrt{3})</math>, and <math>N</math> is at <math>(14,4\sqrt{3})</math>. The distance formula shows that <math>BM=BN=MN=2\sqrt{13}</math>. Therefore, by equilateral triangle area formula, <math>x=13\sqrt{3}</math>, so <math>x^2</math> is <math>\boxed{507}</math>.
+
<asy>
 +
pair A = (0, 0), B = (16, 0), C = (20, 0), D = (8, 8*sqrt(3)), EE = (18, 2*sqrt(3)), M = (9, sqrt(3)), NN = (14, 4*sqrt(3));
 +
draw(A--B--D--cycle);
 +
draw(B--C--EE--cycle);
 +
draw(A--EE);
 +
draw(C--D);
 +
draw(B--M--NN--cycle);
 +
dot(A);
 +
dot(B);
 +
dot(C);
 +
dot(D);
 +
dot(EE);
 +
dot(M);
 +
dot(NN);
 +
label("A", A, SW);
 +
label("B", B, S);
 +
label("C", C, SE);
 +
label("D", D, N);
 +
label("E", EE, N);
 +
label("M", M, NW);
 +
label("N", NN, NE);
 +
</asy>
 +
 
 +
Diagram by [[User:RedFireTruck|<font color="#FF0000">RedFireTruck</font>]] ([[User talk:RedFireTruck|<font color="#FFFFFF">talk</font>]])
 +
 
 +
==Solution 1==
 +
Let <math>A</math> be the origin, so <math>B=(16,0)</math> and <math>C=(20,0).</math> Using equilateral triangle properties tells us that <math>D=(8,8\sqrt3)</math> and <math>E=(18,2\sqrt3)</math> as well. Therefore, <math>M=(9,\sqrt3)</math> and <math>N=(14,4\sqrt3).</math> Applying the Shoelace Theorem to triangle <math>BMN</math> gives
 +
 
 +
<cmath>x=\dfrac 1 2 |16\sqrt3+36\sqrt3+0-(0+14\sqrt3+64\sqrt3)| =13\sqrt3,</cmath>
 +
 
 +
so <math>x^2=\boxed{507}.</math>
 +
 
 
==Solution 2==
 
==Solution 2==
−
Use the same coordinates as above for all points. Then use the Shoelace Formula/Method on triangle <math>BMN</math> to solve for its area.
 
−
 
−
==Solution 3==
 
 
Note that <math>AB=DB=16</math> and <math>BE=BC=4</math>. Also, <math>\angle ABE = \angle DBC = 120^{\circ}</math>. Thus, <math>\triangle ABE \cong \triangle DBC</math> by SAS.
 
Note that <math>AB=DB=16</math> and <math>BE=BC=4</math>. Also, <math>\angle ABE = \angle DBC = 120^{\circ}</math>. Thus, <math>\triangle ABE \cong \triangle DBC</math> by SAS.
  
Line 34: Line 62:
  
 
The other way is to use the Mean Geometry Theorem. Note that <math>\triangle BCE</math> and <math>\triangle BDA</math> are similar and have the same orientation. Note that <math>B</math> is the weighted average of <math>B</math> and <math>B</math>, <math>M</math> is the weighted average of <math>E</math> and <math>A</math>, and <math>N</math> is the weighted average of <math>C</math> and <math>D</math>. The weights are the same for all three averages. (The weights are actually just <math>\frac{1}{2}</math> and <math>\frac{1}{2}</math>, so these are also unweighted averages.) Thus, by the Mean Geometry Theorem, <math>\triangle BMN</math> is similar to both <math>\triangle BAD</math> and <math>\triangle BEC</math>, which means that <math>\triangle BMN</math> is equilateral.
 
The other way is to use the Mean Geometry Theorem. Note that <math>\triangle BCE</math> and <math>\triangle BDA</math> are similar and have the same orientation. Note that <math>B</math> is the weighted average of <math>B</math> and <math>B</math>, <math>M</math> is the weighted average of <math>E</math> and <math>A</math>, and <math>N</math> is the weighted average of <math>C</math> and <math>D</math>. The weights are the same for all three averages. (The weights are actually just <math>\frac{1}{2}</math> and <math>\frac{1}{2}</math>, so these are also unweighted averages.) Thus, by the Mean Geometry Theorem, <math>\triangle BMN</math> is similar to both <math>\triangle BAD</math> and <math>\triangle BEC</math>, which means that <math>\triangle BMN</math> is equilateral.
 +
 +
 +
Note: A much easier way to go about finding <math>BM</math> without having to use Stewart's Theorem is to simply drop the altitudes from M and E to AC, thus hitting AC at points X and Y. Then clearly AEY and AMX are similar with ratio 2. But we know that <math>AY = 18 \implies AX = 9 \implies BX = 16-9 = 7</math>. Additionally, <math>MX = \frac{1}{2} (2\sqrt{3}) = \sqrt{3}</math> from similar triangles meaning we can now just do pythagorean theorem on right triangle <math>MXB</math> to get <math>MB = \sqrt{52}</math> - SuperJJ
 +
 +
==Solution 3==
 +
 +
[[File:2015 AIME I 4.png|430px|right]]
 +
 +
<math> AB = BD, BE = BC, \angle ABE = \angle CBD \implies  \triangle ABE \cong \triangle DBC</math>
 +
 +
Medians are equal, so <math>MB = BN, \angle ABM = \angle DBN \implies</math>
 +
<math>\angle MBN = \angle ABD - \angle ABM + \angle DBN = 60^\circ \implies </math>
 +
 +
<math>\triangle MNB</math> is  equilateral triangle.
 +
 +
The height of <math>\triangle BCE</math> is <math>2 \sqrt{3},</math> distance from <math>A</math> to midpoint <math>BC</math> is <math>16 + 2 = 18 \implies \frac {AE^2}{4} =\frac{ (16 + 2)^2 +2^2 \cdot 3}{4} = 81 + 3 = 84.</math>
 +
 +
<math>BM</math> is the median of <math>\triangle ABE \implies</math>
 +
<math>BM^2 = \frac {AB^2}{2} + \frac {BE^2}{2} - \frac {AE^2}{4}=16 \cdot 8 + 4 \cdot 2 - 84 = 52.</math>
 +
 +
The area of <math>\triangle BMN</math>
 +
 +
<cmath>[BMN] = \frac{\sqrt{3}}{4} BM^2 =13 \sqrt{3} \implies \boxed{\textbf{507}}.</cmath>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
 
==See Also==
 
==See Also==

Latest revision as of 12:45, 17 November 2024

Problem

Point $B$ lies on line segment $\overline{AC}$ with $AB=16$ and $BC=4$. Points $D$ and $E$ lie on the same side of line $AC$ forming equilateral triangles $\triangle ABD$ and $\triangle BCE$. Let $M$ be the midpoint of $\overline{AE}$, and $N$ be the midpoint of $\overline{CD}$. The area of $\triangle BMN$ is $x$. Find $x^2$.

Diagram

[asy] pair A = (0, 0), B = (16, 0), C = (20, 0), D = (8, 8*sqrt(3)), EE = (18, 2*sqrt(3)), M = (9, sqrt(3)), NN = (14, 4*sqrt(3)); draw(A--B--D--cycle); draw(B--C--EE--cycle); draw(A--EE); draw(C--D); draw(B--M--NN--cycle); dot(A); dot(B); dot(C); dot(D); dot(EE); dot(M); dot(NN); label("A", A, SW); label("B", B, S); label("C", C, SE); label("D", D, N); label("E", EE, N); label("M", M, NW); label("N", NN, NE); [/asy]

Diagram by RedFireTruck (talk)

Solution 1

Let $A$ be the origin, so $B=(16,0)$ and $C=(20,0).$ Using equilateral triangle properties tells us that $D=(8,8\sqrt3)$ and $E=(18,2\sqrt3)$ as well. Therefore, $M=(9,\sqrt3)$ and $N=(14,4\sqrt3).$ Applying the Shoelace Theorem to triangle $BMN$ gives

\[x=\dfrac 1 2 |16\sqrt3+36\sqrt3+0-(0+14\sqrt3+64\sqrt3)| =13\sqrt3,\]

so $x^2=\boxed{507}.$

Solution 2

Note that $AB=DB=16$ and $BE=BC=4$. Also, $\angle ABE = \angle DBC = 120^{\circ}$. Thus, $\triangle ABE \cong \triangle DBC$ by SAS.

From this, it is clear that a $60^{\circ}$ rotation about $B$ will map $\triangle ABE$ to $\triangle DBC$. This rotation also maps $M$ to $N$. Thus, $BM=BN$ and $\angle MBN=60^{\circ}$. Thus, $\triangle BMN$ is equilateral.

Using the Law of Cosines on $\triangle ABE$, \[AE^2 = 16^2 + 4^2 - 2\cdot 16\cdot 4\cdot\left(-\frac{1}{2}\right)\] \[AE = 4\sqrt{21}\] Thus, $AM=ME=2\sqrt{21}$.

Using Stewart's Theorem on $\triangle ABE$, \[AM\cdot ME\cdot AE + AE\cdot BM^2 = BE^2\cdot AM + BA^2\cdot ME\] \[BM = 2\sqrt{13}\]

Calculating the area of $\triangle BMN$, \[[BMN] = \frac{\sqrt{3}}{4} BM^2\] \[[BMN] = 13\sqrt{3}\] Thus, $x=13\sqrt{3}$, so $x^2 = 507$. Our final answer is $\boxed{507}$.

Admittedly, this is much more tedious than the coordinate solutions.

I also noticed that there are two more ways of showing that $\triangle BMN$ is equilateral:

One way is to show that $\triangle ADB$, $\triangle BMN$, and $\triangle ECB$ are related by a spiral similarity centered at $B$.

The other way is to use the Mean Geometry Theorem. Note that $\triangle BCE$ and $\triangle BDA$ are similar and have the same orientation. Note that $B$ is the weighted average of $B$ and $B$, $M$ is the weighted average of $E$ and $A$, and $N$ is the weighted average of $C$ and $D$. The weights are the same for all three averages. (The weights are actually just $\frac{1}{2}$ and $\frac{1}{2}$, so these are also unweighted averages.) Thus, by the Mean Geometry Theorem, $\triangle BMN$ is similar to both $\triangle BAD$ and $\triangle BEC$, which means that $\triangle BMN$ is equilateral.


Note: A much easier way to go about finding $BM$ without having to use Stewart's Theorem is to simply drop the altitudes from M and E to AC, thus hitting AC at points X and Y. Then clearly AEY and AMX are similar with ratio 2. But we know that $AY = 18 \implies AX = 9 \implies BX = 16-9 = 7$. Additionally, $MX = \frac{1}{2} (2\sqrt{3}) = \sqrt{3}$ from similar triangles meaning we can now just do pythagorean theorem on right triangle $MXB$ to get $MB = \sqrt{52}$ - SuperJJ

Solution 3

2015 AIME I 4.png

$AB = BD, BE = BC, \angle ABE = \angle CBD \implies \triangle ABE \cong \triangle DBC$

Medians are equal, so $MB = BN, \angle ABM = \angle DBN \implies$ $\angle MBN = \angle ABD - \angle ABM + \angle DBN = 60^\circ \implies$

$\triangle MNB$ is equilateral triangle.

The height of $\triangle BCE$ is $2 \sqrt{3},$ distance from $A$ to midpoint $BC$ is $16 + 2 = 18 \implies \frac {AE^2}{4} =\frac{ (16 + 2)^2 +2^2 \cdot 3}{4} = 81 + 3 = 84.$

$BM$ is the median of $\triangle ABE \implies$ $BM^2 = \frac {AB^2}{2} + \frac {BE^2}{2} - \frac {AE^2}{4}=16 \cdot 8 + 4 \cdot 2 - 84 = 52.$

The area of $\triangle BMN$

\[[BMN] = \frac{\sqrt{3}}{4} BM^2 =13 \sqrt{3} \implies \boxed{\textbf{507}}.\]

vladimir.shelomovskii@gmail.com, vvsss

See Also

2015 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2015_AIME_I_Problems/Problem_4&oldid=234659"