Difference between revisions of "2006 AMC 12A Problems/Problem 13"
m (→See also: typo) |
(→See also) |
||
| Line 15: | Line 15: | ||
{{AMC12 box|year=2006|ab=A|num-b=12|num-a=14}} | {{AMC12 box|year=2006|ab=A|num-b=12|num-a=14}} | ||
| + | {{MAA Notice}} | ||
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
Revision as of 16:52, 3 July 2013
Problem
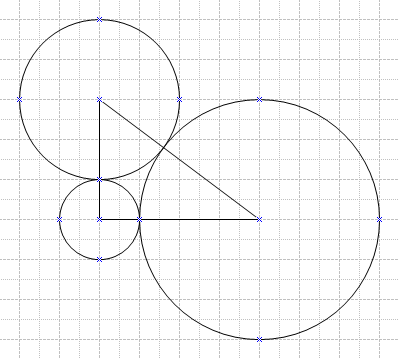
The vertices of a 
right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?
Solution
Let the radius of the smallest circle be 
. We find that the radius of the largest circle is 
and the radius of the second largest circle is 
. Thus, 
. The radii of the other circles are 
and 
. The sum of their areas is 
See also
| 2006 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
