Difference between revisions of "2007 AIME II Problems/Problem 13"
(→Solution) |
m (→Solution: correct typos, rmv {{soln}}) |
||
| Line 5: | Line 5: | ||
== Solution == | == Solution == | ||
| − | + | Label each of the bottom squares as <math>\displaystyle x_0, x_1 \ldots x_9, x_{10}</math>. | |
| − | Label each of the bottom squares as <math>\displaystyle x_0, x_1 \ldots | ||
Through [[induction]], we can find that the top square is equal to <math>{10\choose0}x_0 + {10\choose1}x_1 + {10\choose2}x_2 + \ldots {10\choose10}x_{10}</math>. | Through [[induction]], we can find that the top square is equal to <math>{10\choose0}x_0 + {10\choose1}x_1 + {10\choose2}x_2 + \ldots {10\choose10}x_{10}</math>. | ||
| − | Examine the equation <math>\mod 3</math>. All of the coefficients from <math>\displaystyle x_2 \ldots x_8</math> will be multiples of <math>3</math> (since the numerator will have a <math>9</math>). Thus, the expression boils down to <math>x_0 + 10x_1 + 10x_9 + x_{10} \equiv 0 \mod 3</math>. Reduce to find that <math>x_0 + x_1 + x_9 + x_{10} \equiv 0 \mod 3</math> Out of <math>x_0,\ x_1,\ x_9,\ x_{10}</math>, either all are equal to <math>0</math>, or three of them are equal to <math>1</math>. This gives <math>{4\choose0} + {4\choose3} = 1 + 4 = 5</math> possible combinations of numbers that work. | + | Examine the equation <math>\mod 3</math>. All of the coefficients from <math>\displaystyle x_2 \ldots x_8</math> will be multiples of <math>3</math> (since the numerator will have a <math>9</math>). Thus, the expression boils down to <math>x_0 + 10x_1 + 10x_9 + x_{10} \equiv 0 \mod 3</math>. Reduce to find that <math>x_0 + x_1 + x_9 + x_{10} \equiv 0 \mod 3</math>. Out of <math>x_0,\ x_1,\ x_9,\ x_{10}</math>, either all are equal to <math>0</math>, or three of them are equal to <math>1</math>. This gives <math>{4\choose0} + {4\choose3} = 1 + 4 = 5</math> possible combinations of numbers that work. |
The seven terms from <math>\displaystyle x_2 \ldots x_8</math> can assume either <math>0</math> or <math>1</math>, giving us <math>2^7</math> possibilities. The answer is therefore <math>5 \cdot 2^7 = 640</math>. | The seven terms from <math>\displaystyle x_2 \ldots x_8</math> can assume either <math>0</math> or <math>1</math>, giving us <math>2^7</math> possibilities. The answer is therefore <math>5 \cdot 2^7 = 640</math>. | ||
Revision as of 09:18, 5 April 2007
Problem
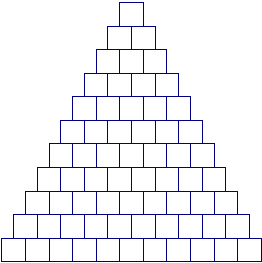
A triangular array of squares has one square in the first row, two in the second, and in general, 
squares in the th row for 
With the exception of the bottom row, each square rests on two squares in the row immediately below (illustrated in given diagram). In each square of the eleventh row, a 
or a 
is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of 's and 's in the bottom row is the number in the top square a multiple of 
?
Solution
Label each of the bottom squares as 
.
Through induction, we can find that the top square is equal to 
.
Examine the equation 
. All of the coefficients from 
will be multiples of (since the numerator will have a 
). Thus, the expression boils down to 
. Reduce to find that 
. Out of 
, either all are equal to , or three of them are equal to . This gives 
possible combinations of numbers that work.
The seven terms from can assume either or , giving us 
possibilities. The answer is therefore 
.
See also
| 2007 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
