Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2003 AMC 12B Problems/Problem 21"

m (→‎Solution 2)
m (→‎Solution 2)
Line 17: Line 17:
 
It follows that <math>0 < \alpha < \frac {\pi}3</math>, and the probability is <math>\frac{\pi/3}{\pi} = \frac 13 \Rightarrow \mathrm{(D)}</math>.
 
It follows that <math>0 < \alpha < \frac {\pi}3</math>, and the probability is <math>\frac{\pi/3}{\pi} = \frac 13 \Rightarrow \mathrm{(D)}</math>.
  
−
==Solution 2==
+
==Solution 2 (Analytic Geometry)==
  
 
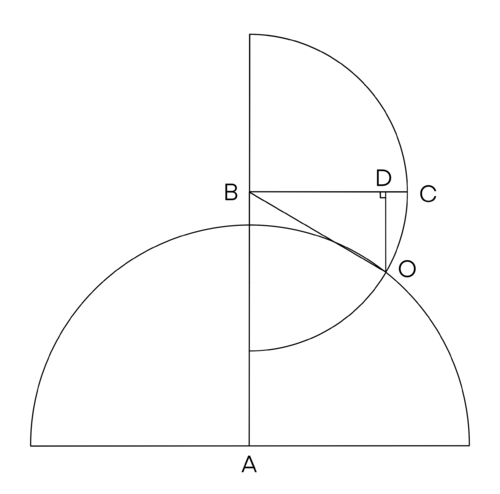
[[File:2003AMC12BP21.png|center|500px]]
 
[[File:2003AMC12BP21.png|center|500px]]
  
 
<math>WLOG</math>, let the object turn clockwise.
 
<math>WLOG</math>, let the object turn clockwise.
 +
 +
Let <math>B = (0, 0)</math>, <math>A = (0, -8)</math>.
  
 
Note that the possible points of <math>C</math> create a semi-circle of radius <math>5</math> and center <math>B</math>. The area where <math>AC < 7</math> is enclosed by a circle of radius <math>7</math> and center <math>A</math>. The probability that <math>AC < 7</math> is <math>\frac{\angle ABO}{180 ^\circ}</math>.
 
Note that the possible points of <math>C</math> create a semi-circle of radius <math>5</math> and center <math>B</math>. The area where <math>AC < 7</math> is enclosed by a circle of radius <math>7</math> and center <math>A</math>. The probability that <math>AC < 7</math> is <math>\frac{\angle ABO}{180 ^\circ}</math>.
  
−
Let <math>B = (0, 0)</math>. The function of <math>\odot B = x^2 + y^2 = 25</math>, the function of <math>\odot A = x^2 + (y+8)^2 = 49</math>.
+
The function of <math>\odot B = x^2 + y^2 = 25</math>, the function of <math>\odot A = x^2 + (y+8)^2 = 49</math>.
  
 
<math>O</math> is the point that satisfies both functions.
 
<math>O</math> is the point that satisfies both functions.

Revision as of 10:57, 31 August 2022

Problem

An object moves $8$ cm in a straight line from $A$ to $B$, turns at an angle $\alpha$, measured in radians and chosen at random from the interval $(0,\pi)$, and moves $5$ cm in a straight line to $C$. What is the probability that $AC < 7$?

$\mathrm{(A)}\ \frac{1}{6} \qquad\mathrm{(B)}\ \frac{1}{5} \qquad\mathrm{(C)}\ \frac{1}{4} \qquad\mathrm{(D)}\ \frac{1}{3} \qquad\mathrm{(E)}\ \frac{1}{2}$

Solution 1 (Trigonometry)

By the Law of Cosines, \begin{align*} AB^2 + BC^2 - 2 AB \cdot BC \cos \alpha = 89 - 80 \cos \alpha = AC^2 &< 49\\ \cos \alpha &> \frac 12\\ \end{align*}

It follows that $0 < \alpha < \frac {\pi}3$, and the probability is $\frac{\pi/3}{\pi} = \frac 13 \Rightarrow \mathrm{(D)}$.

Solution 2 (Analytic Geometry)

2003AMC12BP21.png

$WLOG$, let the object turn clockwise.

Let $B = (0, 0)$, $A = (0, -8)$.

Note that the possible points of $C$ create a semi-circle of radius $5$ and center $B$. The area where $AC < 7$ is enclosed by a circle of radius $7$ and center $A$. The probability that $AC < 7$ is $\frac{\angle ABO}{180 ^\circ}$.

The function of $\odot B = x^2 + y^2 = 25$, the function of $\odot A = x^2 + (y+8)^2 = 49$.

$O$ is the point that satisfies both functions.

$x^2 + (y+8)^2 - x^2 - y^2 = 49 - 25$, $64 + 16y =24$, $y = - \frac52$, $x = \frac{5 \sqrt{3}}{2}$, $O = (\frac{5 \sqrt{3}}{2}, - \frac52)$

Note that $\triangle BDO$ is a $30-60-90$ triangle, as $BO = 5$, $BD = \frac{5 \sqrt{3}}{2}$, $DO = \frac52$. As a result $\angle CBO = 30 ^\circ$, $\angle ABO = 60 ^\circ$.

Therefore the probability that $AC < 7$ is $\frac{\angle ABO}{180 ^\circ} = \frac{60 ^\circ}{180 ^\circ} = \boxed{\textbf{(D) } \frac13 }$

~isabelchen

See also

2003 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 20 		Followed by
Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_12B_Problems/Problem_21&oldid=177780"