Difference between revisions of "2023 AIME I Problems/Problem 5"
MRENTHUSIASM (talk | contribs) (→Solution 7 (Areas and Pythagorean Theorem)) |
m (→Solution 5 (Similar Triangles)) |
||
| Line 121: | Line 121: | ||
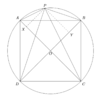
==Solution 5 (Similar Triangles)== | ==Solution 5 (Similar Triangles)== | ||
| − | [[Image:2023_AIME_I_Prob_5_Similar_Triangles.png]] | + | [[Image:2023_AIME_I_Prob_5_Similar_Triangles.png||center|100px]] |
Let the center of the circle be <math>O</math>, and the radius of the circle be <math>r</math>. Since <math>ABCD</math> is a rhombus with diagonals <math>2r</math> and <math>2r</math>, its area is <math>\dfrac{1}{2}(2r)(2r) = 2r^2</math>. Since <math>AC</math> and <math>BD</math> are diameters of the circle, <math>\triangle APC</math> and <math>\triangle BPD</math> are right triangles. Let <math>X</math> and <math>Y</math> be the foot of the altitudes to <math>AC</math> and <math>BD</math>, respectively. We have | Let the center of the circle be <math>O</math>, and the radius of the circle be <math>r</math>. Since <math>ABCD</math> is a rhombus with diagonals <math>2r</math> and <math>2r</math>, its area is <math>\dfrac{1}{2}(2r)(2r) = 2r^2</math>. Since <math>AC</math> and <math>BD</math> are diameters of the circle, <math>\triangle APC</math> and <math>\triangle BPD</math> are right triangles. Let <math>X</math> and <math>Y</math> be the foot of the altitudes to <math>AC</math> and <math>BD</math>, respectively. We have | ||
Revision as of 18:21, 8 February 2023
Contents
- 1 Problem
- 2 Solution 1 (Ptolemy's Theorem)
- 3 Solution 2 (Heights and Half-Angle Formula)
- 4 Solution 3 (Analytic Geometry)
- 5 Solution 4 (Law of Cosines)
- 6 Solution 5 (Similar Triangles)
- 7 Solution 6 (Subtended Chords)
- 8 Solution 7 (Areas and Pythagorean Theorem)
- 9 Solution 8 (Coordinates and Algebraic Manipulation)
- 10 See also
Problem
Let ![]() be a point on the circle circumscribing square
be a point on the circle circumscribing square ![]() that satisfies
that satisfies ![]() and
and ![]() Find the area of
Find the area of ![]()
Solution 1 (Ptolemy's Theorem)
Ptolemy's theorem states that for cyclic quadrilateral ![]() ,
, ![]() .
.
We may assume that ![]() is between
is between ![]() and
and ![]() . Let
. Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . We have
. We have ![]() , because
, because ![]() is a diameter of the circle. Similarly,
is a diameter of the circle. Similarly, ![]() . Therefore,
. Therefore, ![]() . Similarly,
. Similarly, ![]() .
.
By Ptolemy's Theorem on ![]() ,
, ![]() , and therefore
, and therefore ![]() . By Ptolemy's on
. By Ptolemy's on ![]() ,
, ![]() , and therefore
, and therefore ![]() . By squaring both equations, we obtain
. By squaring both equations, we obtain
![]() Thus,
Thus, ![]() , and
, and ![]() . Plugging these values into
. Plugging these values into ![]() , we obtain
, we obtain ![]() , and
, and ![]() . Now, we can solve using
. Now, we can solve using ![]() and
and ![]() (though using
(though using ![]() and
and ![]() yields the same solution for
yields the same solution for ![]() ).
).
 ~mathboy100
~mathboy100
Solution 2 (Heights and Half-Angle Formula)
Drop a height from point ![]() to line
to line ![]() and line
and line ![]() . Call these two points to be
. Call these two points to be ![]() and
and ![]() , respectively. Notice that the intersection of the diagonals of
, respectively. Notice that the intersection of the diagonals of ![]() meets at a right angle at the center of the circumcircle, call this intersection point
meets at a right angle at the center of the circumcircle, call this intersection point ![]() .
.
Since ![]() is a rectangle,
is a rectangle, ![]() is the distance from
is the distance from ![]() to line
to line ![]() . We know that
. We know that ![]() by triangle area and given information. Then, notice that the measure of
by triangle area and given information. Then, notice that the measure of ![]() is half of
is half of ![]() .
.
Using the half-angle formula for tangent,

Solving the equation above, we get that ![]() or
or ![]() . Since this value must be positive, we pick
. Since this value must be positive, we pick ![]() . Then,
. Then, ![]() (since
(since ![]() is a right triangle with line
is a right triangle with line ![]() the diameter of the circumcircle) and
the diameter of the circumcircle) and ![]() . Solving we get
. Solving we get ![]() ,
, ![]() , giving us a diagonal of length
, giving us a diagonal of length ![]() and area
and area ![]() .
.
~Danielzh
Solution 3 (Analytic Geometry)
Denote by ![]() the half length of each side of the square.
We put the square to the coordinate plane, with
the half length of each side of the square.
We put the square to the coordinate plane, with ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
The radius of the circumcircle of ![]() is
is ![]() .
Denote by
.
Denote by ![]() the argument of point
the argument of point ![]() on the circle.
Thus, the coordinates of
on the circle.
Thus, the coordinates of ![]() are
are ![]() .
.
Thus, the equations ![]() and
and ![]() can be written as
can be written as

These equations can be reformulated as

These equations can be reformulated as
![]()
Taking ![]() , by solving the equation, we get
, by solving the equation, we get
![]()
Plugging (3) into (1), we get

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 4 (Law of Cosines)
WLOG, let ![]() be on minor arc
be on minor arc ![]() . Let
. Let ![]() and
and ![]() be the radius and center of the circumcircle respectively, and let
be the radius and center of the circumcircle respectively, and let ![]() .
.
By the Pythagorean Theorem, the area of the square is ![]() . We can use the Law of Cosines on isosceles triangles
. We can use the Law of Cosines on isosceles triangles ![]() to get
to get

Taking the products of the first two and last two equations, respectively, ![]() and
and ![]() Adding these equations,
Adding these equations, ![]() so
so
![]() ~OrangeQuail9
~OrangeQuail9
Solution 5 (Similar Triangles)
Let the center of the circle be ![]() , and the radius of the circle be
, and the radius of the circle be ![]() . Since
. Since ![]() is a rhombus with diagonals
is a rhombus with diagonals ![]() and
and ![]() , its area is
, its area is ![]() . Since
. Since ![]() and
and ![]() are diameters of the circle,
are diameters of the circle, ![]() and
and ![]() are right triangles. Let
are right triangles. Let ![]() and
and ![]() be the foot of the altitudes to
be the foot of the altitudes to ![]() and
and ![]() , respectively. We have
, respectively. We have
![]() so
so ![]() . Similarly,
. Similarly,
![]() so
so ![]() . Since
. Since ![]()
![]()
![]() But
But ![]() is a rectangle, so
is a rectangle, so ![]() , and our similarity becomes
, and our similarity becomes
![]() Cross multiplying and rearranging gives us
Cross multiplying and rearranging gives us ![]() , which rearranges to
, which rearranges to ![]() . Therefore
. Therefore ![]() .
.
~Cantalon
Solution 6 (Subtended Chords)
First draw a diagram.
![[asy] pair A, B, C, D, O, P; A = (0,sqrt(106)); B = (0,0); C = (sqrt(106),0); D = (sqrt(106),sqrt(106)); O = (sqrt(106)/2, sqrt(106)/2); P = intersectionpoint(circle(A, sqrt(212)*sin(atan(28/45)/2)), circle(O, sqrt(212)/2)); draw(A--B--C--D--cycle); draw(circle(O, sqrt(212)/2)); label("$A$", A, NW); label("$B$", B, SW); label("$C$", C, SE); label("$D$", D, NE); label("$P$", P, NW); label("$O$", O, SW); label("$\theta$", O, dir(120)*5); dot(P); dot(O); draw(P--A--C--cycle, red); draw(P--B--D--cycle, blue); draw(P--O); draw(anglemark(P,O,A,30)); [/asy]](http://latex.artofproblemsolving.com/7/6/7/767046b962fc34a9be5e70e9454aa5ccadf915ff.png) Let's say that the radius is
Let's say that the radius is ![]() . Then the area of the
. Then the area of the ![]() is
is ![]() Using the formula for the length of a chord subtended by an angle, we get
Using the formula for the length of a chord subtended by an angle, we get
![]()
![]() Multiplying and simplifying these 2 equations gives
Multiplying and simplifying these 2 equations gives
![]() Similarly
Similarly ![]() and
and ![]() . Again, multiplying gives
. Again, multiplying gives
![]()
![]() Dividing
Dividing ![]() by
by ![]() gives
gives ![]() , so
, so ![]() .
Pluging this back into one of the equations, gives
.
Pluging this back into one of the equations, gives
![\[2r^2 = \dfrac{90}{\cos\left(\tan^{-1}\left(\dfrac{28}{45}\right)\right)}\]](http://latex.artofproblemsolving.com/3/5/2/352d1b973dd4a3b1095b4b16efafe14a2d077548.png) If we imagine a 28-45-53 right triangle, we see that if 28 is opposite and 45 is adjacent,
If we imagine a 28-45-53 right triangle, we see that if 28 is opposite and 45 is adjacent, ![]() . Now we see that
. Now we see that
![]() ~Voldemort101
~Voldemort101
Solution 7 (Areas and Pythagorean Theorem)
By the Inscribed Angle Theorem, we conclude that ![]() and
and ![]() are right triangles.
are right triangles.
Let the brackets denote areas. We are given that
![]() Let
Let ![]() be the center of the circle,
be the center of the circle, ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() and
and ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() as shown below.
as shown below.
![[asy] /* Made by MRENTHUSIASM */ size(200); pair A, B, C, D, O, P, X, Y; A = (-sqrt(106)/2,sqrt(106)/2); B = (-sqrt(106)/2,-sqrt(106)/2); C = (sqrt(106)/2,-sqrt(106)/2); D = (sqrt(106)/2,sqrt(106)/2); O = origin; path p; p = Circle(O,sqrt(212)/2); draw(p); P = intersectionpoints(Circle(A,4),p)[1]; X = foot(P,A,C); Y = foot(P,B,D); draw(A--B--C--D--cycle); draw(P--A--C--cycle,red); draw(P--B--D--cycle,blue); draw(P--X,red+dashed); draw(P--Y,blue+dashed); markscalefactor=0.075; draw(rightanglemark(A,P,C),red); draw(rightanglemark(P,X,C),red); draw(rightanglemark(B,P,D),blue); draw(rightanglemark(P,Y,D),blue); dot("$A$", A, 1.5*NW, linewidth(4)); dot("$B$", B, 1.5*SW, linewidth(4)); dot("$C$", C, 1.5*SE, linewidth(4)); dot("$D$", D, 1.5*NE, linewidth(4)); dot("$P$", P, 1.5*dir(P), linewidth(4)); dot("$X$", X, 1.5*dir(20), linewidth(4)); dot("$Y$", Y, 1.5*dir(Y-P), linewidth(4)); dot("$O$", O, 1.5*E, linewidth(4)); [/asy]](http://latex.artofproblemsolving.com/9/c/0/9c0a09a29f01bde94eeb44ed19b9de1241fe34c2.png) Let
Let ![]() be the diameter of
be the diameter of ![]() It follows that
It follows that
![]() Moreover, note that
Moreover, note that ![]() is a rectangle. The Pythagorean Theorem gives
is a rectangle. The Pythagorean Theorem gives ![]() We rewrite this equation in terms of
We rewrite this equation in terms of ![]()
![]() from which
from which ![]()
Finally, we have ![]()
Solution 8 (Coordinates and Algebraic Manipulation)
![[asy] pair A,B,C,D,P; A=(-3,3); B=(3,3); C=(3,-3); D=(-3,-3); draw(A--B--C--D--cycle); label(A,"$A$",NW); label(B,"$B$",NE); label(C,"$C$",SE); label(D,"$D$",SW); draw(circle((0,0),4.24264068712)); P=(-1,4.12310562562); dot(P); label(P,"$P$", NW); pen k=red+dashed; draw(P--A,k); draw(P--B,k); draw(P--C,k); draw(P--D,k); [/asy]](http://latex.artofproblemsolving.com/9/f/a/9fa54895fd53b9e7d0654c3dec84de03cae0c4bf.png) Let
Let ![]() on the upper quarter of the circle, and let
on the upper quarter of the circle, and let ![]() be the side length of the square. Hence, we want to find
be the side length of the square. Hence, we want to find ![]() . Let the center of the circle be
. Let the center of the circle be ![]() .
The two equations would thus become:
.
The two equations would thus become:
![\[\left(\left(a+\dfrac{k}2\right)^2+\left(b-\dfrac{k}2\right)^2\right)\left(\left(a-\dfrac{k}2\right)^2+\left(b+\dfrac{k}2\right)^2\right)=56^2\]](http://latex.artofproblemsolving.com/c/9/a/c9a90656d3068681df6c5f6cec2775548cf2ab3e.png)
![\[\left(\left(a-\dfrac{k}2\right)^2+\left(b-\dfrac{k}2\right)^2\right)\left(\left(a+\dfrac{k}2\right)^2+\left(b+\dfrac{k}2\right)^2\right)=90^2\]](http://latex.artofproblemsolving.com/6/5/6/656e4665596a25573a3b90fab4a052409dd1a5ca.png) Now, let
Now, let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Our equations now change to
. Our equations now change to ![]() and
and ![]() . Subtracting the first from the second, we have
. Subtracting the first from the second, we have ![]() . Substituting back in and expanding, we have
. Substituting back in and expanding, we have ![]() , so
, so ![]() . We now have one of our terms we need (
. We now have one of our terms we need (![]() ). Therefore, we only need to find
). Therefore, we only need to find ![]() to find
to find ![]() .
We now write the equation of the circle, which point
.
We now write the equation of the circle, which point ![]() satisfies:
satisfies: ![\[a^2+b^2=\left(\dfrac{k\sqrt{2}}{2}\right)^2=\dfrac{k^2}2\]](http://latex.artofproblemsolving.com/4/7/6/476d8f31f266d4c511bc2147e1cda89e8fb33673.png) We can expand the second equation, yielding
We can expand the second equation, yielding ![]() Now, with difference of squares, we get
Now, with difference of squares, we get ![]() . We can add
. We can add ![]() to this equation, which we can factor into
to this equation, which we can factor into ![]() . We realize that
. We realize that ![]() is the same as the equation of the circle, so we plug its equation in:
is the same as the equation of the circle, so we plug its equation in: ![]() . We can combine like terms to get
. We can combine like terms to get ![]() , so
, so ![]() .
Since the answer is an integer, we know
.
Since the answer is an integer, we know ![]() is a perfect square. Since it is even, it is divisible by
is a perfect square. Since it is even, it is divisible by ![]() , so we can factor
, so we can factor ![]() . With some testing with approximations and last-digit methods, we can find that
. With some testing with approximations and last-digit methods, we can find that ![]() . Therefore, taking the square root, we find that
. Therefore, taking the square root, we find that ![]() , the area of square
, the area of square ![]() , is
, is ![]() .
.
~wuwang2002
See also
| 2023 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.