Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AIME I Problems/Problem 12"

(→‎Solution 3 (LOC))
(new solution)
Line 3: Line 3:
  
 
==Solution==
 
==Solution==
 +
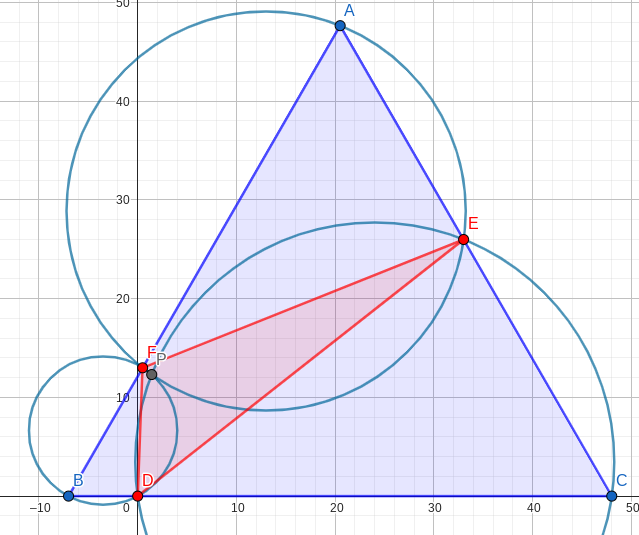
By Miquel's theorem, <math>P=(AEF)\cap(BFD)\cap(CDE)</math>. The law of cosines can be used to compute <math>DE=42</math>, <math>EF=35</math>, and <math>FD=13</math>. Toss the points on the coordinate plane; let <math>B=(-7, 0)</math>, <math>D=(0, 0)</math>, and <math>C=(48, 0)</math>, where we will find <math>\tan^{2}\left(\measuredangle CDP\right)</math> with <math>P=(BFD)\cap(CDE)</math>.
 +
 +
By the extended law of sines, the radius of <math>(BFD)</math> is <math>\frac{13}{2\sin 60^{\circ}}=\frac{13}{3}\sqrt{3}</math>. Its center lies on the line <math>x=-\frac{7}{2}</math>, and the origin is a point on it, so <math>y=\frac{23}{6}\sqrt{3}</math>.
 +
 +
The radius of <math>(CDE)</math> is <math>\frac{42}{2\sin 60^{\circ}}=14\sqrt{3}</math>. The origin is also a point on it, and its center is on the line <math>x=24</math>, so <math>y=2\sqrt{3}</math>.
 +
 +
The equations of the two circles are <cmath>\begin{align*}(BFD)&:\left(x+\tfrac{7}{2}\right)^{2}+\left(y-\tfrac{23}{6}\sqrt{3}\right)^{2}=\tfrac{169}{3} \\ (CDE)&:\left(x-24\right)^{2}+\left(y-2\sqrt{3}\right)^{2}=588\end{align*}</cmath> These equations simplify to <cmath>\begin{align*}(BFD)&:x^{2}+7x+y^{2}-\tfrac{23}{3}\sqrt{3}y=0 \\ (CDE)&: x^{2}-48x+y^{2}-4\sqrt{3}y=0\end{align*}</cmath> Subtracting these two equations gives that both their points of intersection, <math>D</math> and <math>P</math>, lie on the line <math>55x-\tfrac{11}{3}\sqrt{3}y=0</math>. Hence, <math>\tan^{2}\left(\measuredangle AEP\right)=\tan^{2}\left(\measuredangle CDP\right)=\left(\frac{55}{\tfrac{11}{3}\sqrt{3}}\right)^{2}=3\left(\tfrac{55}{11}\right)^{2}=\boxed{075}</math>. To scale, the configuration looks like the figure below.
 +
 +
[[File:AIME 2023-I12 Geogebra Diagram.png]]
 +
 +
==Solution 2==
  
 
Denote <math>\theta = \angle AEP</math>.
 
Denote <math>\theta = \angle AEP</math>.
Line 68: Line 79:
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
  
−
==Solution 2 (no trig)==
+
==Solution 3 (no trig)==
 
Drop the perpendiculars from <math>P</math> to <math>\overline{AB}</math>, <math>\overline{AC}</math>, <math>\overline{BC}</math>, and call them <math>Q,R,</math> and <math>S</math> respectively. This gives us three similar right triangles <math>FQP</math>, <math>ERP</math>, and <math>DSP.</math>  
 
Drop the perpendiculars from <math>P</math> to <math>\overline{AB}</math>, <math>\overline{AC}</math>, <math>\overline{BC}</math>, and call them <math>Q,R,</math> and <math>S</math> respectively. This gives us three similar right triangles <math>FQP</math>, <math>ERP</math>, and <math>DSP.</math>  
  
Line 81: Line 92:
 
~anon
 
~anon
  
−
==Solution 3 (LOC)==
+
==Solution 4 (LOC)==
 
This solution is heavily inspired by AIME 1999 Problem 14 Solution 2 (a similar question)
 
This solution is heavily inspired by AIME 1999 Problem 14 Solution 2 (a similar question)
  

Revision as of 13:19, 9 February 2023

Problem

Let $\triangle ABC$ be an equilateral triangle with side length $55.$ Points $D,$ $E,$ and $F$ lie on $\overline{BC},$ $\overline{CA},$ and $\overline{AB},$ respectively, with $BD = 7,$ $CE=30,$ and $AF=40.$ Point $P$ inside $\triangle ABC$ has the property that \[\angle AEP = \angle BFP = \angle CDP.\] Find $\tan^2(\angle AEP).$

Solution

By Miquel's theorem, $P=(AEF)\cap(BFD)\cap(CDE)$. The law of cosines can be used to compute $DE=42$, $EF=35$, and $FD=13$. Toss the points on the coordinate plane; let $B=(-7, 0)$, $D=(0, 0)$, and $C=(48, 0)$, where we will find $\tan^{2}\left(\measuredangle CDP\right)$ with $P=(BFD)\cap(CDE)$.

By the extended law of sines, the radius of $(BFD)$ is $\frac{13}{2\sin 60^{\circ}}=\frac{13}{3}\sqrt{3}$. Its center lies on the line $x=-\frac{7}{2}$, and the origin is a point on it, so $y=\frac{23}{6}\sqrt{3}$.

The radius of $(CDE)$ is $\frac{42}{2\sin 60^{\circ}}=14\sqrt{3}$. The origin is also a point on it, and its center is on the line $x=24$, so $y=2\sqrt{3}$.

The equations of the two circles are \begin{align*}(BFD)&:\left(x+\tfrac{7}{2}\right)^{2}+\left(y-\tfrac{23}{6}\sqrt{3}\right)^{2}=\tfrac{169}{3} \\ (CDE)&:\left(x-24\right)^{2}+\left(y-2\sqrt{3}\right)^{2}=588\end{align*} These equations simplify to \begin{align*}(BFD)&:x^{2}+7x+y^{2}-\tfrac{23}{3}\sqrt{3}y=0 \\ (CDE)&: x^{2}-48x+y^{2}-4\sqrt{3}y=0\end{align*} Subtracting these two equations gives that both their points of intersection, $D$ and $P$, lie on the line $55x-\tfrac{11}{3}\sqrt{3}y=0$. Hence, $\tan^{2}\left(\measuredangle AEP\right)=\tan^{2}\left(\measuredangle CDP\right)=\left(\frac{55}{\tfrac{11}{3}\sqrt{3}}\right)^{2}=3\left(\tfrac{55}{11}\right)^{2}=\boxed{075}$. To scale, the configuration looks like the figure below.

AIME 2023-I12 Geogebra Diagram.png

Solution 2

Denote $\theta = \angle AEP$.

In $AFPE$, we have $\overrightarrow{AF} + \overrightarrow{FP} + \overrightarrow{PE} + \overrightarrow{EA} = 0$. Thus, \[ AF + FP e^{i \theta} + PE e^{i \left( \theta + 60^\circ \right)} + EA e^{- i 120^\circ} = 0. \]

Taking the real and imaginary parts, we get \begin{align*} AF + FP \cos \theta + PE \cos \left( \theta + 60^\circ \right) + EA \cos \left( - 120^\circ \right) & = 0 \hspace{1cm} (1) \\ FP \sin \theta + PE \sin \left( \theta + 60^\circ \right) + EA \sin \left( - 120^\circ \right) & = 0 \hspace{1cm} (2) \end{align*}

In $BDPF$, analogous to the analysis of $AFPE$ above, we get \begin{align*} BD + DP \cos \theta + PF \cos \left( \theta + 60^\circ \right) + FB \cos \left( - 120^\circ \right) & = 0 \hspace{1cm} (3) \\ DP \sin \theta + PF \sin \left( \theta + 60^\circ \right) + FB \sin \left( - 120^\circ \right) & = 0 \hspace{1cm} (4) \end{align*}

Taking $(1) \cdot \sin \left( \theta + 60^\circ \right) - (2) \cdot \cos \left( \theta + 60^\circ \right)$, we get \[ AF \sin \left( \theta + 60^\circ \right) + \frac{\sqrt{3}}{2} FP - EA \sin \theta = 0 . \hspace{1cm} (5) \]

Taking $(3) \cdot \sin \theta - (4) \cdot \cos \theta$, we get \[ BD \sin \theta - \frac{\sqrt{3}}{2} FP + FB \sin \left( \theta + 120^\circ \right) . \hspace{1cm} (6) \]

Taking $(5) + (6)$, we get \[ AF \sin \left( \theta + 60^\circ \right) - EA \sin \theta + BD \sin \theta + FB \sin \left( \theta + 120^\circ \right) . \]

Therefore, \begin{align*} \tan \theta & = \frac{\frac{\sqrt{3}}{2} \left( AF + FB \right)} {\frac{FB}{2} + EA - \frac{AF}{2} - BD} \\ & = 5 \sqrt{3} . \end{align*}

Therefore, $\tan^2 \theta = \boxed{\textbf{(075) }}$.

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 3 (no trig)

Drop the perpendiculars from $P$ to $\overline{AB}$, $\overline{AC}$, $\overline{BC}$, and call them $Q,R,$ and $S$ respectively. This gives us three similar right triangles $FQP$, $ERP$, and $DSP.$

The sum of the perpendiculars to a point $P$ within an equilateral triangle is always constant, so we have that $PQ+PR+PS=\dfrac{55 \sqrt{3}}{2}.$

The sum of the lengths of the alternating segments split by the perpendiculars from a point $P$ within an equilateral triangle is always equal to half the perimeter, so $QA+RC+SB = \dfrac{165}{2},$ which means that $FQ+ER+DS = QA+RC+SB - CE - AF - BD = \dfrac{165}{2} - 30 - 40 - 7 = \dfrac{11}{2}.$

Finally, $\tan AEP = \dfrac{PQ}{FQ} = \dfrac{PR}{ER} = \dfrac{PS}{DS} = \dfrac{PQ+PR+PS}{FQ+ER+DS} = 5 \sqrt{3}.$

Thus, $\tan^2 AEP = \boxed{075.}$

~anon

Solution 4 (LOC)

This solution is heavily inspired by AIME 1999 Problem 14 Solution 2 (a similar question)

Draw line segments from $P$ to points $A$, $B$, and $C$. And label the angle measure of $\angle{BFP}$, $\angle{CDP}$, and $\angle{AEP}$ to be $\alpha$

Using Law of Cosines (note that $cos{\angle{AFP}}=cos{\angle{BDP}}=cos{\angle{CEP}}=cos{180^\circ-\alpha}=-cos{\alpha}$)

\begin{align*} (1) BP^2 &= FP^2+15^2-2*FP*15*cos(\alpha)\\ (2) BP^2 &= DP^2+7^2+2*DP*7*cos(\alpha)\\ (3) CP^2 &= DP^2+48^2-2*DP*48*cos(\alpha)\\ (4) CP^2 &= EP^2+30^2+2*EP*30*cos(\alpha)\\ (5) AP^2 &= EP^2+25^2-2*EP*25*cos(\alpha)\\ (6) AP^2 &= FP^2+40^2+2*FP*40*cos(\alpha)\\ \end{align*}

We can perform this operation: (1) - (2) + (3) - (4) + (5) - (6)

Leaving us with (after combining and simplifying)

\begin{align*} \cos{\alpha}=\frac{-11}{2*(DP+EP+FP)} \end{align*}

Therefore, we want to solve for $DP+EP+FP$

Notice that $\angle{APC}=\angle{APC}=\angle{APC}=120^\circ$

We can use Law of Cosines again to solve for the sides of $\triangle{DEF}$, which have side lengths of $13$, $42$, and $35$, and area $120\sqrt{3}$.

Label the lengths of $PD$, $PE$, and $PF$ to be $x$, $y$, and $z$.

Therefore, using the $\sin$ area formula,

\begin{align*} [\triangle{DEF}] &= \frac{1}{2}*\sin{120°}*(xy+yz+zx) = 120\sqrt{3} \\ xy+yz+zx &= 2^5*3*5 \end{align*}

In addition, we know that

\begin{align*} x^2+y^2+xy=42^2\\ y^2+z^2+yz=35^2\\ z^2+x^2+zx=13^2\\ \end{align*}

By using Law of Cosines for $\triangle{DPE}$, $\triangle{EPF}$, and $\triangle{FPD}$ respectively

Because we want $DP+EP+FP$, which is $x+y+z$, we see that

\begin{align*} (x+y+z)^2 &= \frac{x^2+y^2+x+y^2+z^2+yz+z^2+x^2+3(zx+xy+yz+zx)}{2} \\ (x+y+z)^2 &= \frac{42^2+35^2+13^2+3*2^5*3*5}{2} \\ (x+y+z)^2 &= 2299 \\ x+y+z &= 11\sqrt{19} \end{align*}

So plugging the results back into the equation before, we get

\begin{align*} \cos{\alpha} = \frac{-1}{2\sqrt{19}}\\ \sin{\alpha} = \frac{5\sqrt{3}}{2\sqrt{19}} \end{align*}

Giving us

\begin{align*} \tan^2{\alpha}=\boxed{075} \end{align*}

~Danielzh

See also

2023 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AIME_I_Problems/Problem_12&oldid=189340"