Difference between revisions of "2003 AMC 8 Problems/Problem 24"
Glowinglol (talk | contribs) (Created page with "The distance from X remains constant for the semicircle, so the first part of the graph has to be a straight line. Then, the line gets closer, and then farther away from X. So, (...") |
Mathisfun7 (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | The distance from X | + | ==Problem== |
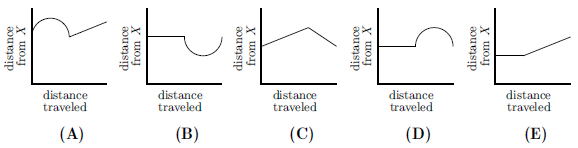
| + | A ship travels from point <math>A</math> to point <math>B</math> along a semicircular path, centered at Island <math>X</math>. Then it travels along a straight path from <math>B</math> to <math>C</math>. Which of these graphs best shows the ship's distance from Island <math>X</math> as it moves along its course? | ||
| + | |||
| + | <asy>size(150); | ||
| + | pair X=origin, A=(-5,0), B=(5,0), C=(0,5); | ||
| + | draw(Arc(X, 5, 180, 360)^^B--C); | ||
| + | dot(X); | ||
| + | label("$X$", X, NE); | ||
| + | label("$C$", C, N); | ||
| + | label("$B$", B, E); | ||
| + | label("$A$", A, W); | ||
| + | </asy> | ||
| + | |||
| + | <center> | ||
| + | [[Image:2003amc8prob24ans.png|800px]] | ||
| + | </center> | ||
| + | |||
| + | ==Solution== | ||
| + | |||
| + | The distance from <math>\text{X}</math> to any point on the semicircle will always be constant. On the graph, this will represent a straight line. The distance between <math>\text{X}</math> and line <math>\text{BC}</math> will not be constant though. We can easily prove that the distance between <math>\text{X}</math> and line <math>\text{BC}</math> will represent a semicircle (prove this by dividing <math>\triangle{XCB}</math> into two congruent triangles using the perpendicular bisector from vertex <math>\text{X}</math>). Since the point on line <math>\text{BC}</math> and the perpendicular bisector from vertex <math>\text{X}</math> is the shortest distance between <math>\text{X}</math> and <math>\text{BC}</math> as well as the midpoint of line <math>\text{BC}</math> it will represent the shortest point on the semicircle in the graph as well as the midpoint of the semicircle. Using the information found, the answer choice that fits them all is <math>\boxed{\text{(B)}}</math>. | ||
| + | |||
| + | {{AMC8 box|year=2003|num-b=23|num-a=25}} | ||
Revision as of 12:03, 24 August 2012
Problem
A ship travels from point ![]() to point
to point ![]() along a semicircular path, centered at Island
along a semicircular path, centered at Island ![]() . Then it travels along a straight path from
. Then it travels along a straight path from ![]() to
to ![]() . Which of these graphs best shows the ship's distance from Island
. Which of these graphs best shows the ship's distance from Island ![]() as it moves along its course?
as it moves along its course?
![[asy]size(150); pair X=origin, A=(-5,0), B=(5,0), C=(0,5); draw(Arc(X, 5, 180, 360)^^B--C); dot(X); label("$X$", X, NE); label("$C$", C, N); label("$B$", B, E); label("$A$", A, W); [/asy]](http://latex.artofproblemsolving.com/9/1/9/91933f8be27c24174af480d964c31782da9f3bb4.png)
Solution
The distance from ![]() to any point on the semicircle will always be constant. On the graph, this will represent a straight line. The distance between
to any point on the semicircle will always be constant. On the graph, this will represent a straight line. The distance between ![]() and line
and line ![]() will not be constant though. We can easily prove that the distance between
will not be constant though. We can easily prove that the distance between ![]() and line
and line ![]() will represent a semicircle (prove this by dividing
will represent a semicircle (prove this by dividing ![]() into two congruent triangles using the perpendicular bisector from vertex
into two congruent triangles using the perpendicular bisector from vertex ![]() ). Since the point on line
). Since the point on line ![]() and the perpendicular bisector from vertex
and the perpendicular bisector from vertex ![]() is the shortest distance between
is the shortest distance between ![]() and
and ![]() as well as the midpoint of line
as well as the midpoint of line ![]() it will represent the shortest point on the semicircle in the graph as well as the midpoint of the semicircle. Using the information found, the answer choice that fits them all is
it will represent the shortest point on the semicircle in the graph as well as the midpoint of the semicircle. Using the information found, the answer choice that fits them all is ![]() .
.
| 2003 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 23 |
Followed by Problem 25 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||