Difference between revisions of "2012 AMC 10B Problems/Problem 14"
Flamedragon (talk | contribs) (→Solution) |
|||
| Line 7: | Line 7: | ||
Thus, answer choice D is correct. | Thus, answer choice D is correct. | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | {{AMC10 box|year=2012|ab=B|num-b=13|num-a=15}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 20:19, 8 February 2014
Solution
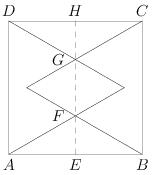
Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length 
and triangle AEF is a 30-60-90 triangle, it follows that EF has length 1. By symmetry, HG also has length 1. Thus GF has length 
. The formula for the area of an equilateral triangle of length s is 
. It follows that the area of the rhombus is:
Thus, answer choice D is correct.
See Also
| 2012 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
