Difference between revisions of "1994 AIME Problems"
m |
|||
| Line 1: | Line 1: | ||
== Problem 1 == | == Problem 1 == | ||
| + | The increasing sequence <math>3, 15, 24, 48, \ldots\,</math> consists of those positive multiples of 3 that are one less than a perfect square. What is the remainder when the 1994th term of the sequence is divided by 1000? | ||
[[1994 AIME Problems/Problem 1|Solution]] | [[1994 AIME Problems/Problem 1|Solution]] | ||
== Problem 2 == | == Problem 2 == | ||
| + | A circle with diameter <math>\overline{PQ}\,</math> of length 10 is internally tangent at <math>P^{}_{}</math> to a circle of radius 20. Square <math>ABCD\,</math> is constructed with <math>A\,</math> and <math>B\,</math> on the larger circle, <math>\overline{CD}\,</math> tangent at <math>Q\,</math> to the smaller circle, and the smaller circle outside <math>ABCD\,</math>. The length of <math>\overline{AB}\,</math> can be written in the form <math>m + \sqrt{n}\,</math>, where <math>m\,</math> and <math>n\,</math> are integers. Find <math>m + n\,</math>. | ||
[[1994 AIME Problems/Problem 2|Solution]] | [[1994 AIME Problems/Problem 2|Solution]] | ||
== Problem 3 == | == Problem 3 == | ||
| + | The function <math>f_{}^{}</math> has the property that, for each real number <math>x,\,</math> | ||
| + | <center><math>f(x)+f(x-1) = x^2\,</math></center>. | ||
| + | If <math>f(19)=94,\,</math> what is the remainder when <math>f(94)\,</math> is divided by 1000? | ||
[[1994 AIME Problems/Problem 3|Solution]] | [[1994 AIME Problems/Problem 3|Solution]] | ||
== Problem 4 == | == Problem 4 == | ||
| + | Find the positive integer <math>n\,</math> for which | ||
| + | <center><math> | ||
| + | \lfloor \log_2{1}\rfloor+\lfloor\log_2{2}\rfloor+\lfloor\log_2{3}\rfloor+\cdots+\lfloor\log_2{n}\rfloor=1994</math></center>. | ||
| + | (For real <math>x\,</math>, <math>\lfloor x\rfloor\,</math> is the greatest integer <math>\le x.\,</math>) | ||
[[1994 AIME Problems/Problem 4|Solution]] | [[1994 AIME Problems/Problem 4|Solution]] | ||
== Problem 5 == | == Problem 5 == | ||
| + | Given a positive integer <math>n\,</math>, let <math>p(n)\,</math> be the product of the non-zero digits of <math>n\,</math>. (If <math>n\,</math> has only one digits, then <math>p(n)\,</math> is equal to that digit.) Let | ||
| + | <center><math>S=p(1)+p(2)+p(3)+\cdots+p(999)</math></center>. | ||
| + | What is the largest prime factor of <math>S\,</math>? | ||
[[1994 AIME Problems/Problem 5|Solution]] | [[1994 AIME Problems/Problem 5|Solution]] | ||
== Problem 6 == | == Problem 6 == | ||
| + | The graphs of the equations | ||
| + | <center><math>y=k, \qquad y=\sqrt{3}x+2k, \qquad y=-\sqrt{3}x+2k,</math></center> | ||
| + | are drawn in the coordinate plane for <math>k=-10,-9,-8,\ldots,9,10.\,</math> These 63 lines cut part of the plane into equilateral triangles of side <math>2/\sqrt{3}.\,</math> How many such triangles are formed? | ||
[[1994 AIME Problems/Problem 6|Solution]] | [[1994 AIME Problems/Problem 6|Solution]] | ||
== Problem 7 == | == Problem 7 == | ||
| − | + | For certain ordered pairs <math>(a,b)\,</math> of real numbers, the system of equations | |
| + | <center><math>ax+by=1\,</math></center> | ||
| + | <center><math>x^2+y^2=50\,</math></center> | ||
| + | has at least one solution, and each solution is an ordered pair <math>(x,y)\,</math> of integers. How many such ordered pairs <math>(a,b)\,</math> are there? | ||
[[1994 AIME Problems/Problem 7|Solution]] | [[1994 AIME Problems/Problem 7|Solution]] | ||
== Problem 8 == | == Problem 8 == | ||
| + | The points <math>(0,0)\,</math>, <math>(a,11)\,</math>, and <math>(b,37)\,</math> are the vertices of an equilateral triangle. Find the value of <math>ab\,</math>. | ||
[[1994 AIME Problems/Problem 8|Solution]] | [[1994 AIME Problems/Problem 8|Solution]] | ||
== Problem 9 == | == Problem 9 == | ||
| + | A solitarire game is played as follows. Six distinct pairs of matched tiles are placed in a bag. The player randomly draws tiles one at a time from the bag and retains them, except that matching tiles are put aside as soon as they appear in the player's hand. The game ends if the player ever holds three tiles, no two of which match; otherwise the drawing continues until the bag is empty. The probability that the bag will be emptied is <math>p/q,\,</math> where <math>p\,</math> and <math>q\,</math> are relatively prime positive integers. Find <math>p+q.\,</math> | ||
[[1994 AIME Problems/Problem 9|Solution]] | [[1994 AIME Problems/Problem 9|Solution]] | ||
== Problem 10 == | == Problem 10 == | ||
| + | In triangle <math>ABC,\,</math> angle <math>C</math> is a right angle and the altitude from <math>C\,</math> meets <math>\overline{AB}\,</math> at <math>D.\,</math> The lengths of the sides of <math>\triangle ABC\,</math> are integers, <math>BD=29^3,\,</math> and <math>\cos B=m/n\,</math>, where <math>m\,</math> and <math>n\,</math> are relatively prime positive integers. Find <math>m+n.\,</math> | ||
[[1994 AIME Problems/Problem 10|Solution]] | [[1994 AIME Problems/Problem 10|Solution]] | ||
== Problem 11 == | == Problem 11 == | ||
| + | Ninety-four bricks, each measuring <math>4''\times10''\times19'',</math> are to stacked one on top of another to form a tower 94 bricks tall. Each brick can be oriented so it contribues <math>4''\,</math> or <math>10''\,</math> or <math>19''\,</math> to the total height of the tower. How many differnt tower heights can be achieved using all 94 of the bricks? | ||
[[1994 AIME Problems/Problem 11|Solution]] | [[1994 AIME Problems/Problem 11|Solution]] | ||
== Problem 12 == | == Problem 12 == | ||
| + | A fenced, rectangular field measures 24 meters by 52 meters. An agricultural researcher has 1994 meters of fence that can be used for internal fencing to partition the field into congruent, square test plots. The entire field must be partitioned, and the sides of the squares must be parallel to the edges of the field. What is the largest number of square test plots into which the field can be partitioned using all or some of the 1994 meters of fence? | ||
[[1994 AIME Problems/Problem 12|Solution]] | [[1994 AIME Problems/Problem 12|Solution]] | ||
== Problem 13 == | == Problem 13 == | ||
| + | The equation | ||
| + | <center><math>x^{10}+(13x-1)^{10}=0\,</math></center> | ||
| + | has 10 complex roots <math>r_1, \overline{r_1}, r_2, \overline{r_2}, r_3, \overline{r_3}, r_4, \overline{r_4}, r_5, \overline{r_5},\,</math> where the bar denotes complex conjugation. Find the value of | ||
| + | <center><math>\frac 1{r_1\overline{r_1}}+\frac 1{r_2\overline{r_2}}+\frac 1{r_3\overline{r_3}}+\frac 1{r_4\overline{r_4}}+\frac 1{r_5\overline{r_5}}.</math></center> | ||
[[1994 AIME Problems/Problem 13|Solution]] | [[1994 AIME Problems/Problem 13|Solution]] | ||
== Problem 14 == | == Problem 14 == | ||
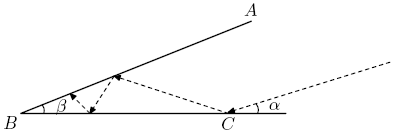
| + | A beam of light strikes <math>\overline{BC}\,</math> at point <math>C\,</math> with angle of incidence <math>\alpha=19.94^\circ\,</math> and reflects with an equal angle of reflection as shown. The light beam continues its path, reflecting off line segments <math>\overline{AB}\,</math> and <math>\overline{BC}\,</math> according to the rule: angle of incidence equals angle of reflection. Given that <math>\beta=\alpha/10=1.994^\circ\,</math> and <math>AB=AC,\,</math> determine the number of times the light beam will bounce off the two line segments. Include the first reflection at <math>C\,</math> in your count. | ||
| + | |||
| + | [[Image:AIME_1994_Problem_14.png]] | ||
[[1994 AIME Problems/Problem 14|Solution]] | [[1994 AIME Problems/Problem 14|Solution]] | ||
== Problem 15 == | == Problem 15 == | ||
| + | Given a point <math>P^{}_{}</math> on a triangular piece of paper <math>ABC,\,</math> consider the creases that are formed in the paper when <math>A, B,\,</math> and <math>C\,</math> are folded onto <math>P.\,</math> Let us call <math>P_{}^{}</math> a fold point of <math>\triangle ABC\,</math> if these creases, which number three unless <math>P^{}_{}</math> is one of the vertices, do not intersect. Suppose that <math>AB=36, AC=72,\,</math> and <math>\angle B=90^\circ.\,</math> Then the area of the set of all fold points of <math>\triangle ABC\,</math> can be written in the form <math>q\pi-r\sqrt{s},\,</math> where <math>q, r,\,</math> and <math>s\,</math> are positive integers and <math>s\,</math> is not divisible by the square of any prime. What is <math>q+r+s\,</math>? | ||
[[1994 AIME Problems/Problem 15|Solution]] | [[1994 AIME Problems/Problem 15|Solution]] | ||
Revision as of 22:49, 28 March 2007
Contents
Problem 1
The increasing sequence ![]() consists of those positive multiples of 3 that are one less than a perfect square. What is the remainder when the 1994th term of the sequence is divided by 1000?
consists of those positive multiples of 3 that are one less than a perfect square. What is the remainder when the 1994th term of the sequence is divided by 1000?
Problem 2
A circle with diameter ![]() of length 10 is internally tangent at
of length 10 is internally tangent at ![]() to a circle of radius 20. Square
to a circle of radius 20. Square ![]() is constructed with
is constructed with ![]() and
and ![]() on the larger circle,
on the larger circle, ![]() tangent at
tangent at ![]() to the smaller circle, and the smaller circle outside
to the smaller circle, and the smaller circle outside ![]() . The length of
. The length of ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() and
and ![]() are integers. Find
are integers. Find ![]() .
.
Problem 3
The function ![]() has the property that, for each real number
has the property that, for each real number ![]()
.
If ![]() what is the remainder when
what is the remainder when ![]() is divided by 1000?
is divided by 1000?
Problem 4
Find the positive integer ![]() for which
for which
.
(For real ![]() ,
, ![]() is the greatest integer
is the greatest integer ![]() )
)
Problem 5
Given a positive integer ![]() , let
, let ![]() be the product of the non-zero digits of
be the product of the non-zero digits of ![]() . (If
. (If ![]() has only one digits, then
has only one digits, then ![]() is equal to that digit.) Let
is equal to that digit.) Let
.
What is the largest prime factor of ![]() ?
?
Problem 6
The graphs of the equations
are drawn in the coordinate plane for ![]() These 63 lines cut part of the plane into equilateral triangles of side
These 63 lines cut part of the plane into equilateral triangles of side ![]() How many such triangles are formed?
How many such triangles are formed?
Problem 7
For certain ordered pairs ![]() of real numbers, the system of equations
of real numbers, the system of equations
has at least one solution, and each solution is an ordered pair ![]() of integers. How many such ordered pairs
of integers. How many such ordered pairs ![]() are there?
are there?
Problem 8
The points ![]() ,
, ![]() , and
, and ![]() are the vertices of an equilateral triangle. Find the value of
are the vertices of an equilateral triangle. Find the value of ![]() .
.
Problem 9
A solitarire game is played as follows. Six distinct pairs of matched tiles are placed in a bag. The player randomly draws tiles one at a time from the bag and retains them, except that matching tiles are put aside as soon as they appear in the player's hand. The game ends if the player ever holds three tiles, no two of which match; otherwise the drawing continues until the bag is empty. The probability that the bag will be emptied is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 10
In triangle ![]() angle
angle ![]() is a right angle and the altitude from
is a right angle and the altitude from ![]() meets
meets ![]() at
at ![]() The lengths of the sides of
The lengths of the sides of ![]() are integers,
are integers, ![]() and
and ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 11
Ninety-four bricks, each measuring ![]() are to stacked one on top of another to form a tower 94 bricks tall. Each brick can be oriented so it contribues
are to stacked one on top of another to form a tower 94 bricks tall. Each brick can be oriented so it contribues ![]() or
or ![]() or
or ![]() to the total height of the tower. How many differnt tower heights can be achieved using all 94 of the bricks?
to the total height of the tower. How many differnt tower heights can be achieved using all 94 of the bricks?
Problem 12
A fenced, rectangular field measures 24 meters by 52 meters. An agricultural researcher has 1994 meters of fence that can be used for internal fencing to partition the field into congruent, square test plots. The entire field must be partitioned, and the sides of the squares must be parallel to the edges of the field. What is the largest number of square test plots into which the field can be partitioned using all or some of the 1994 meters of fence?
Problem 13
The equation
has 10 complex roots ![]() where the bar denotes complex conjugation. Find the value of
where the bar denotes complex conjugation. Find the value of
Problem 14
A beam of light strikes ![]() at point
at point ![]() with angle of incidence
with angle of incidence ![]() and reflects with an equal angle of reflection as shown. The light beam continues its path, reflecting off line segments
and reflects with an equal angle of reflection as shown. The light beam continues its path, reflecting off line segments ![]() and
and ![]() according to the rule: angle of incidence equals angle of reflection. Given that
according to the rule: angle of incidence equals angle of reflection. Given that ![]() and
and ![]() determine the number of times the light beam will bounce off the two line segments. Include the first reflection at
determine the number of times the light beam will bounce off the two line segments. Include the first reflection at ![]() in your count.
in your count.
Problem 15
Given a point ![]() on a triangular piece of paper
on a triangular piece of paper ![]() consider the creases that are formed in the paper when
consider the creases that are formed in the paper when ![]() and
and ![]() are folded onto
are folded onto ![]() Let us call
Let us call ![]() a fold point of
a fold point of ![]() if these creases, which number three unless
if these creases, which number three unless ![]() is one of the vertices, do not intersect. Suppose that
is one of the vertices, do not intersect. Suppose that ![]() and
and ![]() Then the area of the set of all fold points of
Then the area of the set of all fold points of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. What is
is not divisible by the square of any prime. What is ![]() ?
?