Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1992 AIME Problems/Problem 10"
(→‎Solution)
 
Line 12: Line 12:
 
<center>[[Image:AIME_1992_Solution_10.png]]</center>
 
<center>[[Image:AIME_1992_Solution_10.png]]</center>
  
−
We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is <math>40^2-\frac{40^2}{4}-\frac{1}{2}\pi 20^2\approx 571.68</math>
+
To find the area outside the two circles but inside the square, we want to find the unique area of the two circles. We can do this by adding the area of the two circles and then subtracting out their overlap. There are two methods of finding the area of overlap:
 +
 
 +
1. Consider that the area is just the quarter-circle with radius <math>20</math> minus an isosceles right triangle with base length <math>20</math>, and then doubled (to consider the entire overlapped area)
 +
 
 +
2. Consider that the circles can be converted into polar coordinates, and their equations are <math>r = 40sin\theta</math> and <math>r = 40cos\theta</math>. Using calculus with the appropriate bounds, we can compute the overlapped area.
 +
 
 +
Using either method, we compute the overlapped area to be <math>200\pi + 400</math>, and so the area of the intersection of those three graphs is <math>40^2-(200\pi + 400) \Rightarrow 1200 - 200\pi \approx 571.68</math>
  
 
<math>\boxed{572}</math>
 
<math>\boxed{572}</math>
 +
 
== See also ==
 
== See also ==
 
{{AIME box|year=1992|num-b=9|num-a=11}}
 
{{AIME box|year=1992|num-b=9|num-a=11}}

Latest revision as of 11:05, 16 July 2019

Problem

Consider the region $A$ in the complex plane that consists of all points $z$ such that both $\frac{z}{40}$ and $\frac{40}{\overline{z}}$ have real and imaginary parts between $0$ and $1$, inclusive. What is the integer that is nearest the area of $A$?

Solution

Let $z=a+bi \implies \frac{z}{40}=\frac{a}{40}+\frac{b}{40}i$. Since $0\leq \frac{a}{40},\frac{b}{40}\leq 1$ we have the inequality \[0\leq a,b \leq 40\]which is a square of side length $40$.

Also, $\frac{40}{\overline{z}}=\frac{40}{a-bi}=\frac{40a}{a^2+b^2}+\frac{40b}{a^2+b^2}i$ so we have $0\leq a,b \leq \frac{a^2+b^2}{40}$, which leads to:\[(a-20)^2+b^2\geq 20^2\] \[a^2+(b-20)^2\geq 20^2\]

We graph them:

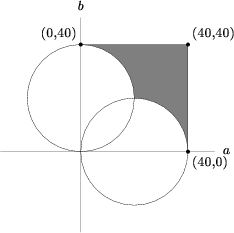
AIME 1992 Solution 10.png

To find the area outside the two circles but inside the square, we want to find the unique area of the two circles. We can do this by adding the area of the two circles and then subtracting out their overlap. There are two methods of finding the area of overlap:

1. Consider that the area is just the quarter-circle with radius $20$ minus an isosceles right triangle with base length $20$, and then doubled (to consider the entire overlapped area)

2. Consider that the circles can be converted into polar coordinates, and their equations are $r = 40sin\theta$ and $r = 40cos\theta$. Using calculus with the appropriate bounds, we can compute the overlapped area.

Using either method, we compute the overlapped area to be $200\pi + 400$, and so the area of the intersection of those three graphs is $40^2-(200\pi + 400) \Rightarrow 1200 - 200\pi \approx 571.68$

$\boxed{572}$

See also

1992 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 9 		Followed by
Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1992_AIME_Problems/Problem_10&oldid=107675"