Difference between revisions of "Angle Bisector Theorem"

Revision as of 14:51, 13 October 2006

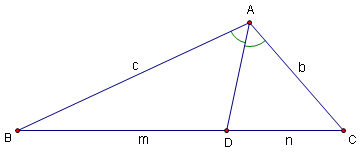
Introduction

The Angle Bisector Theorem states that given triangle $\triangle ABC$ and angle bisector AD, where D is on side BC, then $\frac cm = \frac bn$ . Likewise, the converse of this theorem holds as well.

Proof

Method 1

Because of the ratios and equal angles in the theorem, we think of similar triangles. There are not any similar triangles in the figure as it now stands, however. So, we think to draw in a carefully chosen line or two. Extending AD until it hits the line through C parallel to AB does just the trick:

Since AB and CE are parallel, we know that $\angle BAE=\angle CEA$ and $\angle BCE=\angle ABC$ . Triangle ACE is isosceles, meaning that AC = CE.

By AA similarity, $\triangle DAB \cong \triangle DEC$ . By the properties of similar triangles, we arrive at our desired result:

$\frac cm = \frac bn.$

Method 2

Let $AD = d$ . Now, we can express the area of triangle ABD in two ways:

$[ABD] = \frac 12 cd\sin \angle BAD = \frac 12 md \sin \angle ADB.$

Thus, $\frac{\sin \angle ADB}{\sin \angle BAD} = \frac cm$ .

Likewise, triangle ACD can be expressed in two different ways:

$[ACD] = \frac 12 bd \sin \angle CAD = \frac 12 dn \sin \angle ADC.$

Thus, $\frac{\sin \angle ADC}{\sin \angle CAD} = \frac bn$ .

But $\angle CAD \cong \angle BAD$ and $\sin \angle ADC = \sin \angle ADB$ since $\angle ADC = \pi - \angle ADB$ . Therefore, we can substitute back into our previous equation to get $\frac{\sin \angle ADB}{\sin \angle BAD} = \frac bn$ .

We conclude that $\frac{\sin \angle ADB}{\sin \angle BAD} = \frac cm = \frac bn$ , which was what we wanted.

In both cases, if we reverse all the steps, we see that everything still holds and thus the converse holds.

Examples

Let ABC be a triangle with angle bisector AD with D on line segment BC. If $BD = 2, CD = 5,$ and $AB + AC = 10$ , find AB and AC.
Solution: By the angle bisector theorem, $\frac{AB}2 = \frac{AC}5$ or $AB = \frac 25 AC$ . Plugging this into $AB + AC = 10$ and solving for AC gives $AC = \frac{50}7$ . We can plug this back in to find $AB = \frac{20}7$ .
In triangle ABC, let P be a point on BC and let $AB = 20, AC = 10, BP = \frac{20\sqrt{3}}3, CP = \frac{10\sqrt{3}}3$ . Find the value of $m\angle BAP - m\angle CAP$ .
Solution: First, we notice that $\frac{AB}{BP}=\frac{AC}{CP}$ . Thus, AP is the angle bisector of angle A, making our answer 0.

@@ Line 6: / Line 6: @@
 == Proof ==
 ===Method 1 ===
-Because of the ratios and equal angles in the theorem, we think of similar triangles.  There are not any similar triangles in the figure as it now stands, however.  So, we think to draw in a carefully chosen line or two.  Extending AD until it hits the line through C parallel to AB does just the trick as we shall see!
+Because of the [[ratio]]s and equal [[angle]]s in the theorem, we think of [[similarity | similar]] triangles.  There are not any similar triangles in the figure as it now stands, however.  So, we think to draw in a carefully chosen line or two.  Extending AD until it hits the line through C [[parallel]] to AB does just the trick:
 <center>[[image:Anglebisectortheorem.PNG]]</center>
-Since AB and CE are parallel, we know that <math> \angle BAE=\angle CEA </math> and <math> \angle BCE=\angle ABC </math>.  Triangle ACE is isosceles, meaning that AC = CE.
+Since AB and CE are parallel, we know that <math> \angle BAE=\angle CEA </math> and <math> \angle BCE=\angle ABC </math>.  Triangle ACE is [[isosceles triangle | isosceles]], meaning that AC = CE.
-By AA, <math> \triangle DAB \cong \triangle DEC </math>.  By the properties of similar triangles, we arrive at our desired result:
+By [[AA similarity]], <math> \triangle DAB \cong \triangle DEC </math>.  By the properties of similar triangles, we arrive at our desired result:
 <center><math> \frac cm = \frac bn.</math> </center>

Page

Toolbox

Search